Article contents
Nonlinear evolution and secondary instability of steady and unsteady Görtler vortices induced by free-stream vortical disturbances
Published online by Cambridge University Press: 25 September 2017
Abstract
We study the nonlinear development and secondary instability of steady and unsteady Görtler vortices which are excited by free-stream vortical disturbances (FSVD) in a boundary layer over a concave wall. The focus is on low-frequency (long-wavelength) components of FSVD, to which the boundary layer is most receptive. For simplification, FSVD are modelled by a pair of oblique modes with opposite spanwise wavenumbers  $\pm k_{3}$, and their intensity is strong enough (but still of low level) that the excitation and evolution of Görtler vortices are nonlinear. For the general case that the Görtler number
$\pm k_{3}$, and their intensity is strong enough (but still of low level) that the excitation and evolution of Görtler vortices are nonlinear. For the general case that the Görtler number 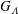 $G_{\unicode[STIX]{x1D6EC}}$ (based on the spanwise wavelength
$G_{\unicode[STIX]{x1D6EC}}$ (based on the spanwise wavelength  $\unicode[STIX]{x1D6EC}$ of the disturbances) is
$\unicode[STIX]{x1D6EC}$ of the disturbances) is 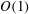 $O(1)$, the formation and evolution of Görtler vortices are governed by the nonlinear unsteady boundary-region equations, supplemented by appropriate upstream and far-field boundary conditions, which characterize the impact of FSVD on the boundary layer. This initial-boundary-value problem is solved numerically. FSVD excite steady and unsteady Görtler vortices, which undergo non-modal growth, modal growth and nonlinear saturation for FSVD of moderate intensity. However, for sufficiently strong FSVD the modal stage is bypassed. Nonlinear interactions cause Görtler vortices to saturate, with the saturated amplitude being independent of FSVD intensity when
$O(1)$, the formation and evolution of Görtler vortices are governed by the nonlinear unsteady boundary-region equations, supplemented by appropriate upstream and far-field boundary conditions, which characterize the impact of FSVD on the boundary layer. This initial-boundary-value problem is solved numerically. FSVD excite steady and unsteady Görtler vortices, which undergo non-modal growth, modal growth and nonlinear saturation for FSVD of moderate intensity. However, for sufficiently strong FSVD the modal stage is bypassed. Nonlinear interactions cause Görtler vortices to saturate, with the saturated amplitude being independent of FSVD intensity when 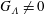 $G_{\unicode[STIX]{x1D6EC}}\neq 0$. The predicted modified mean-flow profiles and structure of Görtler vortices are in excellent agreement with several steady experimental measurements. As the frequency increases, the nonlinearly generated harmonic component
$G_{\unicode[STIX]{x1D6EC}}\neq 0$. The predicted modified mean-flow profiles and structure of Görtler vortices are in excellent agreement with several steady experimental measurements. As the frequency increases, the nonlinearly generated harmonic component 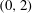 $(0,2)$ (which has zero frequency and wavenumber
$(0,2)$ (which has zero frequency and wavenumber 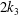 $2k_{3}$) becomes larger, and as a result the Görtler vortices appear almost steady. The secondary instability analysis indicates that Görtler vortices become inviscidly unstable in the presence of FSVD with a high enough intensity. Three types of inviscid unstable modes, referred to as sinuous (odd) modes I, II and varicose (even) modes I, are identified, and their relevance is delineated. The characteristics of dominant unstable modes, including their frequency ranges and eigenfunctions, are in good agreement with experiments. The secondary instability is intermittent when FSVD are unsteady and of low frequency. However, the intermittence diminishes as the frequency increases. The present theoretical framework, which allows for a detailed and integrated description of the key transition processes, from generation, through linear and nonlinear evolution, to the onset of secondary instability, represents a useful step towards predicting the pre-transitional flow and transition itself of the boundary layer over a blade in turbomachinery.
$2k_{3}$) becomes larger, and as a result the Görtler vortices appear almost steady. The secondary instability analysis indicates that Görtler vortices become inviscidly unstable in the presence of FSVD with a high enough intensity. Three types of inviscid unstable modes, referred to as sinuous (odd) modes I, II and varicose (even) modes I, are identified, and their relevance is delineated. The characteristics of dominant unstable modes, including their frequency ranges and eigenfunctions, are in good agreement with experiments. The secondary instability is intermittent when FSVD are unsteady and of low frequency. However, the intermittence diminishes as the frequency increases. The present theoretical framework, which allows for a detailed and integrated description of the key transition processes, from generation, through linear and nonlinear evolution, to the onset of secondary instability, represents a useful step towards predicting the pre-transitional flow and transition itself of the boundary layer over a blade in turbomachinery.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 42
- Cited by



