Article contents
From Rayleigh–Bénard convection to porous-media convection: how porosity affects heat transfer and flow structure
Published online by Cambridge University Press: 18 May 2020
Abstract
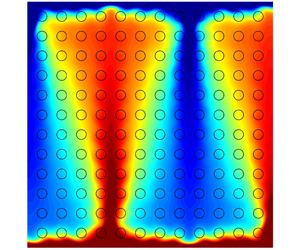
We perform a numerical study of the heat transfer and flow structure of Rayleigh–Bénard (RB) convection in (in most cases regular) porous media, which are comprised of circular, solid obstacles located on a square lattice. This study is focused on the role of porosity  $\unicode[STIX]{x1D719}$ in the flow properties during the transition process from the traditional RB convection with
$\unicode[STIX]{x1D719}$ in the flow properties during the transition process from the traditional RB convection with  $\unicode[STIX]{x1D719}=1$ (so no obstacles included) to Darcy-type porous-media convection with
$\unicode[STIX]{x1D719}=1$ (so no obstacles included) to Darcy-type porous-media convection with  $\unicode[STIX]{x1D719}$ approaching 0. Simulations are carried out in a cell with unity aspect ratio, for Rayleigh number
$\unicode[STIX]{x1D719}$ approaching 0. Simulations are carried out in a cell with unity aspect ratio, for Rayleigh number  $Ra$ from
$Ra$ from  $10^{5}$ to
$10^{5}$ to  $10^{10}$ and varying porosities
$10^{10}$ and varying porosities  $\unicode[STIX]{x1D719}$, at a fixed Prandtl number
$\unicode[STIX]{x1D719}$, at a fixed Prandtl number  $Pr=4.3$, and we restrict ourselves to the two-dimensional case. For fixed
$Pr=4.3$, and we restrict ourselves to the two-dimensional case. For fixed  $Ra$, the Nusselt number
$Ra$, the Nusselt number  $Nu$ is found to vary non-monotonically as a function of
$Nu$ is found to vary non-monotonically as a function of  $\unicode[STIX]{x1D719}$; namely, with decreasing
$\unicode[STIX]{x1D719}$; namely, with decreasing  $\unicode[STIX]{x1D719}$, it first increases, before it decreases for
$\unicode[STIX]{x1D719}$, it first increases, before it decreases for  $\unicode[STIX]{x1D719}$ approaching 0. The non-monotonic behaviour of
$\unicode[STIX]{x1D719}$ approaching 0. The non-monotonic behaviour of  $Nu(\unicode[STIX]{x1D719})$ originates from two competing effects of the porous structure on the heat transfer. On the one hand, the flow coherence is enhanced in the porous media, which is beneficial for the heat transfer. On the other hand, the convection is slowed down by the enhanced resistance due to the porous structure, leading to heat transfer reduction. For fixed
$Nu(\unicode[STIX]{x1D719})$ originates from two competing effects of the porous structure on the heat transfer. On the one hand, the flow coherence is enhanced in the porous media, which is beneficial for the heat transfer. On the other hand, the convection is slowed down by the enhanced resistance due to the porous structure, leading to heat transfer reduction. For fixed  $\unicode[STIX]{x1D719}$, depending on
$\unicode[STIX]{x1D719}$, depending on  $Ra$, two different heat transfer regimes are identified, with different effective power-law behaviours of
$Ra$, two different heat transfer regimes are identified, with different effective power-law behaviours of  $Nu$ versus
$Nu$ versus  $Ra$, namely a steep one for low
$Ra$, namely a steep one for low  $Ra$ when viscosity dominates, and the standard classical one for large
$Ra$ when viscosity dominates, and the standard classical one for large  $Ra$. The scaling crossover occurs when the thermal boundary layer thickness and the pore scale are comparable. The influences of the porous structure on the temperature and velocity fluctuations, convective heat flux and energy dissipation rates are analysed, further demonstrating the competing effects of the porous structure to enhance or reduce the heat transfer.
$Ra$. The scaling crossover occurs when the thermal boundary layer thickness and the pore scale are comparable. The influences of the porous structure on the temperature and velocity fluctuations, convective heat flux and energy dissipation rates are analysed, further demonstrating the competing effects of the porous structure to enhance or reduce the heat transfer.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 41
- Cited by


