Article contents
Acoustic propagation and scattering in the exhaust flow from coaxial cylinders
Published online by Cambridge University Press: 01 October 2008
Abstract
In this paper we present an analytical solution to the problem of sound radiation from semi-infinite coaxial cylinders, as a model for rearward noise emission by aeroengines. The cylinders carry uniform subsonic flows, whose Mach numbers may differ from each other and from that of the external flow. The incident field takes the form of a downstream-going acoustic mode in either the outer cylinder (the bypass flow) or the inner cylinder (the jet). The key geometrical ingredient of our problem is that the two open ends are staggered by a finite axial distance, so that the inner cylinder can be either buried upstream inside the outer cylinder, or can protrude downstream beyond the end of the outer cylinder (sometimes called the ‘half-cowl’ configuration). The solution is found by solving a matrix Wiener–Hopf equation, which involves the factorization of a certain matrix 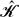 in the form
in the form 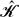 −
−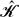 =
= 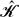 +, with
+, with 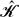 ± analytic, invertible and with algebraic behaviour at infinity in the upper and lower halves of the complex Fourier plane respectively. It turns out that the method of solution is different for the buried and protruding cases. In the buried case the well-known pole removal technique can be applied to a certain meromorphic function (denoted k11), but in the protruding case the corresponding function k22 is no longer meromorphic. Progress is made, however, by using a Padé representation of k22 to yield a meromorphic problem which can then be solved using the pole removal technique as before. A range of results is presented, for both buried and protruding systems and with and without mean flow, and it becomes clear that the stagger of the two open ends can have a very significant effect on the far-field noise. We also obtain reasonable agreement between our predictions and some experimental results. One particular noise mechanism we identify in the presence of mean shear is the way in which a Kelvin–Helmholtz instability mode launched from the upstream trailing edge can be scattered into sound by its interaction with the downstream edge, provided that the separation between the edges is sufficiently large in a way which we identify.
± analytic, invertible and with algebraic behaviour at infinity in the upper and lower halves of the complex Fourier plane respectively. It turns out that the method of solution is different for the buried and protruding cases. In the buried case the well-known pole removal technique can be applied to a certain meromorphic function (denoted k11), but in the protruding case the corresponding function k22 is no longer meromorphic. Progress is made, however, by using a Padé representation of k22 to yield a meromorphic problem which can then be solved using the pole removal technique as before. A range of results is presented, for both buried and protruding systems and with and without mean flow, and it becomes clear that the stagger of the two open ends can have a very significant effect on the far-field noise. We also obtain reasonable agreement between our predictions and some experimental results. One particular noise mechanism we identify in the presence of mean shear is the way in which a Kelvin–Helmholtz instability mode launched from the upstream trailing edge can be scattered into sound by its interaction with the downstream edge, provided that the separation between the edges is sufficiently large in a way which we identify.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
REFERENCES
- 48
- Cited by


