Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-21T18:17:52.640Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Hardy-Hille and Mehler formulas

Published online by Cambridge University Press:  18 May 2009

W. A. Al-Salam  and
L. Carlitz
W. A. Al-Salam
Affiliation:
Texas Technological CollegeLubbockTexas, U.S.A.
L. Carlitz
Affiliation:
Duke University DurhamN. Carolina, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 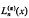and Hn(x) be the nth Laguerre and Hermite polynomials, respectively. Two well-known bilinear generating formulas are the Hardy-Hille formula [1, p. 101]

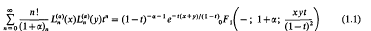
and the mehler formula [1, p. 377]

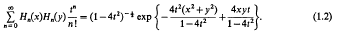
This suggests the following problem. Consider the equation

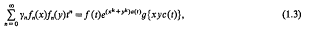
where fa(x) is a polynomial in x of degree n with highest coefficient equal to 1,

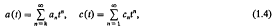
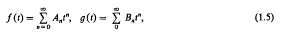
A0 = B0 = 1. We shall also assume that ak = 1 and y0y1y2 … yk–1 ≠ 0. We seek all sets of polynomials {fn(x)} which satisfy (1.3), (1.4) and (1.5).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 7 , Issue 1 , January 1965 , pp. 55 - 60
Copyright
Copyright © Glasgow Mathematical Journal Trust 1965

References

1.Szegó, G., Orthogonal polynomials, American Mathematical Society Colloquium Publications. vol. 23, Revised edition, New York, 1959.Google Scholar