Article contents
The convolution x-r*xs
Published online by Cambridge University Press: 18 May 2009
Extract
In a recent paper [1], Jones extended the definition of the convolution of distributions so that further convolutions could be defined. The convolution w1*w2 of two distributions w1 and w2 was defined as the limit ofithe sequence {wln*w2n}, provided the limit w exists in the sense that
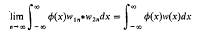
for all fine functions ф in the terminology of Jones [2], where
w1n(x) = wl(x)τ(x/n), W2n(x) = w2(x)τ(x/n)
and τ is an infinitely differentiable function satisfying the following conditions:
(i) τ(x) = τ(—x),
(ii)0 ≤ τ (x) ≤ l,
(iii)τ (x) = l for |x| ≤ ½,
(iv) τ (x) = 0 for |x| ≥ 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1976
References
REFERENCES
- 2
- Cited by


