Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T19:28:36.879Z Has data issue: false hasContentIssue false
  • English
  • Français

NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT

Part of: Model theory Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Diophantine equations

Published online by Cambridge University Press:  14 August 2015

RAF CLUCKERS ,
GEORGES COMTE  and
FRANÇOIS LOESER
RAF CLUCKERS
Affiliation:
Université Lille 1, Laboratoire Painlevé, CNRS - UMR 8524, Cité Scientifique, 59655 Villeneuve d’Ascq Cedex, France Katholieke Universiteit Leuven, Department of Mathematics, Celestijnenlaan 200B, B-3001 Leuven, Belgium; Raf.Cluckers@math.univ-lille1.fr
GEORGES COMTE
Affiliation:
Université Savoie Mont Blanc, LAMA, CNRS UMR 5127, F-73000 Chambéry, France; Georges.Comte@univ-savoie.fr
FRANÇOIS LOESER
Affiliation:
Sorbonne Universités, UPMC Univ Paris 06, UMR 7586 CNRS, Institut Mathématique de Jussieu, F-75005 Paris, France; Francois.Loeser@upmc.fr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove an analog of the Yomdin–Gromov lemma for 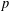$p$-adic definable sets and more broadly in a non-Archimedean definable context. This analog keeps track of piecewise approximation by Taylor polynomials, a nontrivial aspect in the totally disconnected case. We apply this result to bound the number of rational points of bounded height on the transcendental part of 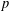$p$-adic subanalytic sets, and to bound the dimension of the set of complex polynomials of bounded degree lying on an algebraic variety defined over 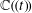$\mathbb{C}(\!(t)\!)$, in analogy to results by Pila and Wilkie, and by Bombieri and Pila, respectively. Along the way we prove, for definable functions in a general context of non-Archimedean geometry, that local Lipschitz continuity implies piecewise global Lipschitz continuity.

MSC classification

Primary: 03C98: Applications of model theory 11D88: $p$-adic and power series fields
Secondary: 11G50: Heights 14G05: Rational points
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 3 , 2015 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Bélair, L., Macintyre, A. and Scanlon, T., ‘Model theory of the Frobenius on the Witt vectors’, Amer. J. Math. 129 (2007), 665–721.CrossRefGoogle Scholar
Bombieri, E. and Pila, J., ‘The number of integral points on arcs and ovals’, Duke Math. J. 59 (1989), 337–357.CrossRefGoogle Scholar
Broberg, N., ‘A note on a paper by R. Heath-Brown: ‘The density of rational points on curves and surfaces’’, J. Reine Angew. Math. 571 (2004), 159–178.Google Scholar
Browning, T., Heath-Brown, D. and Salberger, P., ‘Counting rational points on algebraic varieties’, Duke Math. J. 132 (2006), 545–578.CrossRefGoogle Scholar
Burguet, D., ‘A proof of Yomdin–Gromov’s algebraic lemma’, Israel J. Math. 168 (2008), 291–316.CrossRefGoogle Scholar
Chambert-Loir, A. and Loeser, F., ‘Motivic height zeta functions’, Amer. J. Math., to appear. arXiv:1302.2077.Google Scholar
Chatzidakis, Z., van den Dries, L. and Macintyre, A., ‘Definable sets over finite fields’, J. Reine Angew. Math. 427 (1992), 107–135.Google Scholar
Cilleruelo, J. and Shparlinski, I., ‘Concentration of points on curves in finite fields’, Monatsh. Math. 171 (2013), 315–327.CrossRefGoogle Scholar
Cluckers, R., ‘Analytic p-adic cell decomposition and integrals’, Trans. Amer. Math. Soc. 356 (2004), 1489–1499.CrossRefGoogle Scholar
Cluckers, R., Comte, G. and Loeser, F., ‘Lipschitz continuity properties for p-adic semialgebraic and subanalytic functions’, Geom. Funct. Anal. 20 (2010), 68–87.CrossRefGoogle Scholar
Cluckers, R. and Halupczok, I., ‘Approximations and Lipschitz continuity in p-adic semialgebraic and subanalytic geometry’, Selecta Math. (N.S.) 18 (2012), 825–837.CrossRefGoogle Scholar
Cluckers, R. and Lipshitz, L., ‘Fields with analytic structure’, J. Eur. Math. Soc. 13 (2011), 1147–1223.CrossRefGoogle Scholar
Cluckers, R. and Lipshitz, L., ‘Strictly convergent analytic structures’, J. Eur. Math. Soc., to appear. arXiv:1312.5932.Google Scholar
Cluckers, R., Lipshitz, L. and Robinson, Z., ‘Analytic cell decomposition and analytic motivic integration’, Ann. Sci. Éc. Norm. Supér (4) 39 (2006), 535–568.CrossRefGoogle Scholar
Cluckers, R. and Loeser, F., ‘b-minimality’, J. Math. Log. 7 (2007), 195–227.CrossRefGoogle Scholar
Cohen, S. D., ‘The distribution of Galois groups and Hilbert’s irreducibility theorem’, Proc. Lond. Math. Soc. (3) 43 (1981), 227–250.CrossRefGoogle Scholar
Cox, D., Little, J. and O’Shea, D., Ideals, Varieties, and Algorithms (Springer, New York, 1992).CrossRefGoogle Scholar
Denef, J., ‘p-adic semialgebraic sets and cell decomposition’, J. Reine Angew. Math. 369 (1986), 154–166.Google Scholar
Denef, J. and van den Dries, L., ‘p-adic and real subanalytic sets’, Ann. of Math. (2) 128 (1988), 79–138.CrossRefGoogle Scholar
van den Dries, L., Tame Topology and o-Minimal Structures, London Mathematical Society Lecture Notes Series, 248 (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Gromov, M., ‘Entropy, homology and semialgebraic geometry’, inSéminaire Bourbaki, Vol. 1985/1986, Astérisque, 145–146 (1987), 225–240.Google Scholar
Halupczok, I., ‘Non-archimedean Whitney stratifications’, Proc. Lond. Math. Soc. (3) 109 (2014), 1304–1362.CrossRefGoogle Scholar
Heath-Brown, D., ‘The density of rational points on curves and surfaces’, Ann. of Math. (2) 155 (2002), 553–595.CrossRefGoogle Scholar
Hsu, C., ‘A large sieve inequality for rational function fields’, J. Number Theory 58 (1996), 267–287.CrossRefGoogle Scholar
Macintyre, A., ‘On definable subsets of p-adic fields’, J. Symbolic Logic 41 (1976), 605–610.CrossRefGoogle Scholar
Marmon, O., ‘A generalization of the Bombieri–Pila determinant method’, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 377 (2010); Issled. Teorii Chisel. 10, 63–77, 242; translation in J. Math. Sci. (N. Y.) 171 (2010), 736–744.Google Scholar
Mourgues, M.-H., ‘Cell decomposition for P-minimal fields’, Math. Logic Quart. 55 (2009), 487–492.CrossRefGoogle Scholar
Pas, J., ‘Uniform p-adic cell decomposition and local zeta-functions’, J. Reine Angew. Math. 399 (1989), 137–172.Google Scholar
Pas, J., ‘Cell decomposition and local zeta functions in a tower of unramified extensions of a p-adic field’, Proc. Lond. Math. Soc. (3) 60(1) (1990), 37–67.CrossRefGoogle Scholar
Pila, J., ‘Density of integral and rational points on varieties’, inColumbia University Number Theory Seminar (New York, 1992), Astérisque, 228 (1995), 183–187.Google Scholar
Pila, J., ‘Integer points on the dilation of a subanalytic surface’, Q. J. Math. 55 (2004), 207–223.Google Scholar
Pila, J., ‘The density of rational points on a Pfaff curve’, Ann. Fac. Sci. Toulouse Math. (6) 16(3) (2007), 635–645.CrossRefGoogle Scholar
Pila, J., ‘On the algebraic points of a definable set’, Selecta Math. (N. S.) 15 (2009), 151–170.CrossRefGoogle Scholar
Pila, J., ‘o-minimality and the André-Oort conjecture for ℂn’, Ann. of Math. (2) 173 (2011), 1779–1840.CrossRefGoogle Scholar
Pila, J. and Wilkie, A., ‘The rational points of a definable set’, Duke Math. J. 133 (2006), 591–616.CrossRefGoogle Scholar
Rideau, S., ‘Some properties of analytic difference fields’, J. Inst. Math. Jussieu, to appear. arXiv:1401.1765.Google Scholar
Salberger, P., ‘On the density of rational and integral points on algebraic varieties’, J. reine angew. Math. 606 (2007), 123–147.Google Scholar
Scanlon, T., ‘A proof of the André-Oort conjecture via mathematical logic’, inSéminaire Bourbaki, 2010–2011, Astérisque, 348 (2012).Google Scholar
Scanlon, T., ‘Counting special points: logic, diophantine geometry, and transcendence theory’, Bull. Amer. Math. Soc. (N. S.) 49 (2012), 51–71.CrossRefGoogle Scholar
Scanlon, T., ‘o-minimality as an approach to the André-Oort conjecture, Panoramas et Synthèses’ (to appear).Google Scholar
Serre, J.-P., Lectures on the Mordell-Weil Theorem, Aspects of Mathematics (Vieweg, Braunschweig, 1997).CrossRefGoogle Scholar
Yomdin, Y., ‘Volume growth and entropy’, Israel J. Math. 57 (1987), 285–300.CrossRefGoogle Scholar
Yomdin, Y., ‘Ck -resolution of semialgebraic mappings. Addendum to: ‘Volume growth and entropy’’, Israel J. Math. 57 (1987), 301–317.CrossRefGoogle Scholar
Zannier, U., ‘Some problems of unlikely intersections in arithmetic and geometry’, inAnnals of Mathematics Studies, Vol. 181 (Princeton University Press, Princeton, NJ, 2012): with appendixes by D. Masser.Google Scholar