Hostname: page-component-7bb8b95d7b-pwrkn Total loading time: 0 Render date: 2024-09-21T15:31:40.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Tracial Rokhlin property for automorphisms on simple -algebras

Published online by Cambridge University Press:  01 August 2008

HUAXIN LIN  and
HIROYUKI OSAKA
HUAXIN LIN
Affiliation:
Department of Mathematics, East China Normal University, Shanghai, China University of Oregon, Eugene, Oregon 97403-1222, USA
HIROYUKI OSAKA
Affiliation:
Department of Mathematical Sciences, Ritsumeikan University, Kusatsu, Shiga, 525-8577, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be a unital simple -algebra of real rank zero. Given an isomorphismγ1:K1(A)→K1(A), we show that there is an automorphism α:A→A such that α*1=γ1 and α has the tracial Rokhlin property. Consequently, the crossed product 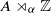is a simple unital AH-algebra with real rank zero. We also show that automorphisms with the Rokhlin property can be constructed from minimal homeomorphisms on a connected compact metric space.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 4 , August 2008 , pp. 1215 - 1241
Copyright
Copyright © 2008 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Brown, L. G. and Pedersen, G. P.. C *-algebras of real rank zero. J. Funct. Anal. 99 (1991), 131–149.CrossRefGoogle Scholar
[2]Connes, A.. Outer conjugacy classes of automorphisms of factors. Ann. Sci. Éc. Norm. Sup. Ser. 4 8 (1975), 383–420.Google Scholar
[3]Elliott, G. A.. On the classification of C *-algebras of real rank zero. J. Reine Angew Math. 443 (1993), 179–219.Google Scholar
[4]Elliott, G. A. and Gong, G.. On the classification of C *-algebras of real rank zero, II. Ann. of Math. 144 (1996), 497–610.CrossRefGoogle Scholar
[5]Elliott, G. A. and Gong, G.. On inductive limit of matrix algebras over the two-torus. Amer. J. Math. 118 (1996), 263–290.CrossRefGoogle Scholar
[6]Goodearl, K. R.. Notes on a class of simple C *-algebras with real rank zero. Publ. Math. 36 (1992), 637–654.CrossRefGoogle Scholar
[7]Gong, G. and Lin, H.. Almost multiplicative morphisms and K-theory. Internat. J. Math. 11 (2000), 983–1000.CrossRefGoogle Scholar
[8]Herman, R. H. and Ocneanu, A.. Stability for integer actions on UHF C *-algebras. J. Funct. Anal. 59 (1984), 132–144.CrossRefGoogle Scholar
[9]Halmos, P. R. and Vaughan, H. E.. The marriage problem. Amer. J. Math. 72 (1950), 214–215.CrossRefGoogle Scholar
[10]Iwanik, A., Lemańczyk, M. and Rudolph, D.. Absolutely continuous cocycles over irrational rotations. Israel J. Math. 83 (1993), 73–95.CrossRefGoogle Scholar
[11]Izumi, M.. The Rohlin property for automorphisms of C *-algebras. Mathematical Physics in Mathematics and Physics (Siena, 2000) (Fields Inst. Commun., 30). American Mathematical Society, Providence RI, 2001, pp. 191–206.Google Scholar
[12]Izumi, M.. Finite group actions on C *-algebras with the Rohlin property. I. Duke Math. J. 122(2) (2004), 233–280.CrossRefGoogle Scholar
[13]Ji, R.. On the crossed product C *-algebras associated with Furstenberg transformations on tori, Dissertation, State University of New York, Stony Brook, 1986.Google Scholar
[14]Kishimoto, A.. The Rohlin property for automorphisms of UHF algebras. J. Reine Angew. Math. 465 (1995), 183–196.Google Scholar
[15]Kishimoto, A.. Automorphisms of -algebras with the Rohlin property. J. Operator Theory 40 (1988), 277–294.Google Scholar
[16]Kishimoto, A.. Unbounded derivations in AT algebras. J. Funct. Anal. 160 (1998), 270–311.CrossRefGoogle Scholar
[17]Lin, H.. Homomorphisms from C *-algebras of continuous trace. Math. Scand. 86 (2000), 249–272.CrossRefGoogle Scholar
[18]Lin, H.. Classification of simple tracially AF C *-algebras. Canad. J. Math. 53 (2001), 161–194.CrossRefGoogle Scholar
[19]Lin, H.. An Introduction to the Classification of Amenable C*-Algebras. World Scientific, Singapore, 2001.Google Scholar
[20]Lin, H.. Simple C *-algebras with unique tracial states and quantized topological spaces. Acta Math. Sin. (Engl. Ser.) 18 (2002), 181–198.CrossRefGoogle Scholar
[21]Lin, H.. Classification of simple C *-algebras with tracial topological rank zero. Duke Math. J. 125 (2004), 91–119.CrossRefGoogle Scholar
[22]Lin, H.. Classification of homomorphisms and dynamical systems. Trans. Amer. Math. Soc. 359 (2007), 859–895.CrossRefGoogle Scholar
[23]Lin, H.. Minimal homeomorphisms and approximate conjugacy in measure. Illinois J. Math. to appear, arXiv:math.OA/0501262.Google Scholar
[24]Lin, H.. The Rokhlin property for automorphisms on simple C *-algebras. Operator Theory, Operator Algebras, and Applications (Contemporary Mathematics, 414). American Mathematical Society, Providence, RI, 2006, pp. 189–215.CrossRefGoogle Scholar
[25]Lin, H. and Osaka, H.. The Rokhlin property and the tracial topological rank. J. Funct. Anal. 218 (2005), 475–494.CrossRefGoogle Scholar
[26]Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115 (2000), 1–24.CrossRefGoogle Scholar
[27]Nakamura, H.. Aperiodic automorphisms of certain simple C *-algebras. Operator Algebras and Applications (Advanced Studies in Pure Mathematics, 38). Mathematical Society of Japan, Tokyo, 2004, pp. 145–157.Google Scholar
[28]Osaka, H. and Phillips, N. C.. Stable and real rank for crossed products by automorphisms with the tracial Rokhlin property. Ergod. Th. & Dynam. Sys. 26 (2006), 1579–1621.CrossRefGoogle Scholar
[29]Osaka, H. and Phillips, N. C.. Furstenberg transformations on irrational rotation algebras. Ergod. Th. & Dynam. Sys. 26 (2006), 1623–1651.CrossRefGoogle Scholar
[30]Phillips, N. C.. Crossed products by finite cyclic group actions with the tracial Rokhlin property. Preprint, arXiv:math.OA/0306410.Google Scholar
[31]Phillips, N. C.. The tracial Rokhlin property is generic, in preparation.Google Scholar
[32]Rørdam, M.. Classification of certain infinite simple C *-algebras. J. Funct. Anal. 131 (1995), 415–458.CrossRefGoogle Scholar
[33]Thomsen, K.. On isomorphisms of inductive limit C *-algebras. Proc. Amer. Math. Soc. 113 (1991), 947–953.Google Scholar
[34]Wegge-Olsen, N. E.. K-Theory and C *-Algebras. A Friendly Approach. Oxford University Press, New York, 1993.CrossRefGoogle Scholar