Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-19T11:35:40.950Z Has data issue: false hasContentIssue false
  • English
  • Français

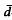-Convergence to equilibrium and space—time bernoullicity for spin systems in the M < ε case

Published online by Cambridge University Press:  19 September 2008

Jeffrey E. Steif
Jeffrey E. Steif
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Liggett has proved that for spin systems, Markov processes with state space {0,1}ℤn, there is a unique stationary distribution in the M < ε regime and all initial configurations uniformly approach this unique stationary distribution exponentially in the weak topology. Here, M and ε are two parameters of the system. We extend this result to discrete time but strengthen it by proving exponential convergence in the stronger 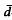- metric instead of the usual weak topology. This is then used to show that the unique stationary process with state space {0,1}ℤn and index set ℤ is isomorphic (in the sense of ergodic theory) to an independent process indexed by ℤ. In the translation invariant case, we prove the stronger fact that this stationary process viewed as a {0, l}-valued process with index set ℤn × ℤ (spacetime) is isomorphic to an independent process also indexed by ℤn × ℤ. This shows that this process is in some sense the most random possible. An application of this last result to approximating by an infinite number of finite systems concatenated independently together is also presented. Finally, we extend all of these results to continuous time.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 11 , Issue 3 , September 1991 , pp. 547 - 575
Copyright
Copyright © Cambridge University Press 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, Scot. (1991), Very weak Bernoulli for amenable groups. Israel J. Math, submitted. Preprint.Google Scholar
Conze, J. P., (1972), Entropie déun group abelien de transformations. Z. Wahrscheinlichkeitstheorie und Vew. Gebiete 25 11–30.CrossRefGoogle Scholar
Ethier, Stewart N., & Kurtz, Thomas G. (1986), Markov Processes—Characterization and Convergence, John Wiley & Sons, New York.CrossRefGoogle Scholar
Furstenberg, H., (1981), Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton.CrossRefGoogle Scholar
Gray, Laurence, (1978), Controlled spin-flip systems. Ann. Probability 6 953–974.CrossRefGoogle Scholar
Katznelson, Y., & Weiss, B., (1972), Commuting measure-preserving transformations. Israel J. Math. 12 161–173.CrossRefGoogle Scholar
Lebowitz, J. L., Maes, C., & Speer, E., (1990), Statistical mechanics of probabilistic cellular automata, J. Statist. Phys. 59 117–170.CrossRefGoogle Scholar
Liggett, Thomas M., (1985), Interacting Particle Systems, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Ornstein, Donald S. (1974), Ergodic Theory, Randomness and Dynamical Systems. Yale University Press, New Haven.Google Scholar
Ornstein, Donald S., & Weiss, B., (1974), Finitely determined implies very weak Bernoulli. Israel J. Math. 17 94–104.CrossRefGoogle Scholar
Ornstein, Donald S., & Weiss, B., (1987), Entropy and isomorphism theorems for actions of amenable groups. J. d'Analyse Mathématique 48 1–141.CrossRefGoogle Scholar
Rosenblatt, Murray, (1971), Markov Processes. Structure and Asymptotic Behavior. Springer-Verlag, New York.Google Scholar
Steif, Jeffrey E., (1988), The ergodic structure of interacting particle systems. Doctoral Dissertation, Department of Mathematics, Stanford University.Google Scholar
Steif, Jeffrey E., (1991), Space-time Bernoullicity of the lower and upper stationary processe s for attractive spin systems. Ann. Probab. to be printed.CrossRefGoogle Scholar
Sullivan, W. G., (1974), A unified existence and ergodic theorem for Markov evolution of random fields. Z. Wahrscheinlichkeitstheorie und Vew. Gebiete 31 47–56.CrossRefGoogle Scholar
Thouvenot, J. P., (1972), Convergence en moyenne de l'information pour l'action de ℤ2. Z. Wahrscheinlichkeitstheorie und Vew. Gebiete 24 135–137.CrossRefGoogle Scholar
Walters, Peter, (1975), An Introduction to Ergodic Theory. Springer-Verlag, New York.Google Scholar