No CrossRef data available.
Article contents
A Limit Proof of the Theorem Euc. III, 35
Published online by Cambridge University Press: 31 October 2008
Extract
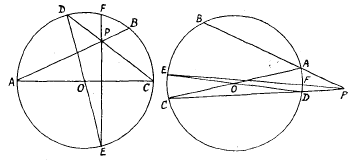
Let AB be any chord passing through the fixed point P. Draw the diameter AOC, join CP and let it meet the circumference at D Then in triangle ACP, AC2 = AP2 + CP2 together with either 2AP. PB or 2 CP. PD according as CP is projected on AP or AP on CP. Hence AP.PB = CP.PD. Now draw the diameter DOE, join EP and let it meet the circumference at F. Then the theorem is true for chords CD. EF.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1925


