Articles
Partially Identified Econometric Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 181-240
-
- Article
- Export citation
The Calculation of the Limiting Distribution of the Least-Squares Estimator in a Near-Integrated Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 241-255
-
- Article
- Export citation
Testing for Unit Roots in Time Series Data
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 256-271
-
- Article
- Export citation
Consistency Via Type 2 Inequalities: A Generalization of Wu's Theorem
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 272-286
-
- Article
- Export citation
Et Interview
Interviewed by Peter E. Rossi
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 287-317
-
- Article
- Export citation
Problems
A Switching Regression Model with Imperfect Sample Separation and Several Regimes
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 319
-
- Article
- Export citation
Unbiased Prediction in a Simple Simultaneous Equations Model
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 320
-
- Article
- Export citation
Results for a Simple Triangular Simultaneous Equations Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 320-321
-
- Article
- Export citation
Solutions
Structural Estimation under Partial Identification1
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 321-324
-
- Article
- Export citation
Testing Linear Restrictions with Unequal Variances
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 324-326
-
- Article
- Export citation
An Alternative Heteroscedastic Error Components Model
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 326
-
- Article
- Export citation
Results on LIML for an Equation Identified by Means of (within equation) Linear Restrictions
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 326-328
-
- Article
- Export citation
Estimation of an Error in Variable Autoregressive Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 328-331
-
- Article
- Export citation
Front matter
ECT volume 5 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

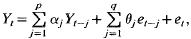 for
for 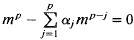 satisfy the hypothesis
satisfy the hypothesis 