Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-27T22:23:30.759Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone Subsequences in High-Dimensional Permutations

Part of: Designs and configurations

Published online by Cambridge University Press:  16 October 2017

NATHAN LINIAL  and
MICHAEL SIMKIN
NATHAN LINIAL
Affiliation:
School of Computer Science and Engineering, The Hebrew University of Jerusalem, Jerusalem 91904, Israel (e-mail: nati@cs.huji.ac.il)
MICHAEL SIMKIN
Affiliation:
Institute of Mathematics and Federmann Center for the Study of Rationality, The Hebrew University of Jerusalem, Jerusalem 91904, Israel (e-mail: menahem.simkin@mail.huji.ac.il)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is part of the ongoing effort to study high-dimensional permutations. We prove the analogue to the Erdős–Szekeres theorem: For every k ≥ 1, every order-nk-dimensional permutation contains a monotone subsequence of length Ωk(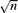$\sqrt{n}$), and this is tight. On the other hand, and unlike the classical case, the longest monotone subsequence in a random k-dimensional permutation of order n is asymptotically almost surely Θk(nk/(k+1)).

MSC classification

Primary: 05B15: Orthogonal arrays, Latin squares, Room squares
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 1 , January 2018 , pp. 69 - 83
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Baik, J., Deift, P. and Johansson, K. (1999) On the distribution of the length of the longest increasing subsequence of random permutations. J. Amer. Math. Soc. 12 1119–1178.Google Scholar
[2] Baker, R. C., Harman, G. and Pintz, J. (2001) The difference between consecutive primes II. Proc. London Math. Soc. 83 532–562.CrossRefGoogle Scholar
[3] Bollobás, B. and Winkler, P. (1988) The longest chain among random points in Euclidean space. In Proc. Amer. Math. Soc. 103 347–353.CrossRefGoogle Scholar
[4] Dilworth, R. P. (1950) A decomposition theorem for partially ordered sets. Ann. of Math. 51 161–166.CrossRefGoogle Scholar
[5] Erdős, P. and Szekeres, G. (1935) A combinatorial problem in geometry. Compositio Math. 2 463–470.Google Scholar
[6] Hammersley, J. (1972) A few seedlings of research. In Proc. Sixth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, pp. 345–394.Google Scholar
[7] Impagliazzo, R. and Kabanets, V. (2010) Constructive proofs of concentration bounds. In Approximation, Randomization, and Combinatorial Optimization: Algorithms and Techniques (Serna, M. et al., eds), Springer, pp. 617–631.Google Scholar
[8] Jacobson, M. T. and Matthews, P. (1996) Generating uniformly distributed random Latin squares. J. Combin. Designs 4 405–437.Google Scholar
[9] Kruskal, J. B. (1953) Monotonic subsequences. Proc. Amer. Math. Soc. 4 264–274.Google Scholar
[10] Linial, N. and Luria, Z. (2014) On the vertices of the d-dimensional Birkhoff polytope. Discrete Comput. Geom. 51 161–170.Google Scholar
[11] Linial, N. and Luria, Z. (2014) An upper bound on the number of high-dimensional permutations. Combinatorica 34 471–486.Google Scholar
[12] Logan, B. F. and Shepp, L. A. (1977) A variational problem for random Young tableaux. Adv. Math. 26 206–222.CrossRefGoogle Scholar
[13] Mirsky, L. (1971) A dual of Dilworth's decomposition theorem. Amer. Math. Monthly 78 876–877.CrossRefGoogle Scholar
[14] Steele, J. M. (1995) Variations on the monotone subsequence theme of Erdős and Szekeres. In Discrete Probability and Algorithms (Aldous, D. et al., eds), Springer, pp. 111–131.CrossRefGoogle Scholar
[15] Szabó, T. and Tardos, G. (2001) A multidimensional generalization of the Erdős–Szekeres lemma on monotone subsequences. Combin. Probab. Comput. 10 557–565.Google Scholar
[16] Ulam, S. M. (1961) Monte Carlo calculations in problems of mathematical physics. In Modern Mathematics for the Engineer: Second Series (Beckenbach, E. F., ed.), McGraw-Hill, pp. 261–281.Google Scholar
[17] Vershik, A. M. and Kerov, S. V. (1977) Asymptotics of the Plancherel measure of the symmetric group and the limiting form of Young tables. Doklady Akademii Nauk SSSR 233 1024–1027.Google Scholar