Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T16:13:59.292Z Has data issue: false hasContentIssue false
  • English
  • Français

On the decay of singular inner functions

Part of: Classical measure theory Function theory on the disc

Published online by Cambridge University Press:  02 December 2020

Thomas Ransford
Thomas Ransford*
Affiliation:
Département de mathématiques et de statistique, Université Laval, Québec, QCG1V 0A6, Canada
*
e-mail:ransford@mat.ulaval.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that if $S(z)$ is a non-constant singular inner function defined on the unit disk, then 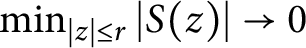$\min _{|z|\le r}|S(z)|\to 0$ as 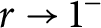$r\to 1^-$ . We show that the convergence can be arbitrarily slow.

Keywords

Singular inner functionHausdorff measure

MSC classification

Primary: 30J15: Singular inner functions
Secondary: 28A78: Hausdorff and packing measures
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 902 - 905
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by grants from NSERC and the Canada research chairs program.

References

Carleson, L., Selected problems on exceptional sets . Van Nostrand Mathematical Studies, 13, Van Nostrand, Princeton, NJ, 1967.Google Scholar
Mashreghi, J., Derivatives of inner functions . Fields Institute Monographs, 31, Springer, New York NY, 2013. http://dx.doi.org/10.1007/978-1-4614-5611-7 Google Scholar