Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T01:13:23.312Z Has data issue: false hasContentIssue false
  • English
  • Français

On Parseval Wavelet Frames with Two or Three Generators via the Unitary Extension Principle

Published online by Cambridge University Press:  20 November 2018

Ole Christensen ,
Hong Oh Kim  and
Rae Young Kim
Ole Christensen
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800 Lyngby, Denmark e-mail: ochr@dtu.dk
Hong Oh Kim
Affiliation:
Department of Mathematical Sciences, KAIST Guseong-dong, Yuseong-gu, Daejeon, 305-701, Republic of Korea e-mail: kimhong@kaist.edu
Rae Young Kim
Affiliation:
Department of Mathematics, Yeungnam University, Dae-dong, Gyeongsan-si, Gyeongsangbuk-do, 712-749, Republic of Korea e-mail: rykim@ynu.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The unitary extension principle 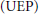$\left( \text{UEP} \right)$ by A. Ron and Z. Shen yields a sufficient condition for the construction of Parseval wavelet frames with multiple generators. In this paper we characterize the 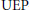$\text{UEP}$-type wavelet systems that can be extended to a Parseval wavelet frame by adding just one 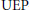$\text{UEP}$-type wavelet system. We derive a condition that is necessary for the extension of a UEP-type wavelet system to any Parseval wavelet frame with any number of generators and prove that this condition is also sufficient to ensure that an extension with just two generators is possible.

Keywords

42C1542C40Bessel sequencesframesextension of wavelet Bessel system to tight framewavelet systemsunitary extension principle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 254 - 263
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

This research was supported by the Yeungnam University research grants in 2010.

References

[1] Casazza, P. and Leonhard, N., Classes of finite equal norm Parseval frames. Contemp. Math. 451 (2008, 11–31.10.1090/conm/451/08755CrossRefGoogle Scholar
[2] Charina, M., Putinar, M., Scheiderer, C., and Stöckler, J., A real algebra perspective on multivariate tight wavelet frames. Preprint, 2012.10.1007/s00365-013-9191-5CrossRefGoogle Scholar
[3] Christensen, O., Frames and bases. An introductory course. Birkhäuser, Boston, 2008.Google Scholar
[4] Christensen, O., Kim, H. O., and Kim, R. Y., Extensions of Bessel sequences to dual pairs of frames. Appl. Comput. Harmon. Anal. 34 (2013, 224–233.http://dx.doi.org/10.1016/j.acha.2012.04.003 CrossRefGoogle Scholar
[5] Chui, C., He, W., and Stöckler, J., Compactly supported tight and sibling frames with maximum vanishing moments. Appl. Comput. Harmon. Anal. 13 (2002, 226–262.http://dx.doi.org/10.1016/S1063-5203(02)00510-9 CrossRefGoogle Scholar
[6] Daubechies, I., Ten Lectures on Wavelets. SIAM, Philadelphia, PA, 1992.Google Scholar
[7] Daubechies, I., Han, B., Ron, A., and Shen, Z., Framelets: MRA-based constructions of wavelet frames. Appl. Comput. Harmon. Anal. 14 (2003, 1–42.http://dx.doi.org/10.1016/S1063-5203(02)00511-0 CrossRefGoogle Scholar
[8] Han, B., Matrix splitting with symmetry and symmetric tight framelet filter banks with two high-pass filters. Appl. Comput. Harmon. Anal.http://dx.doi.org/10.1016/j.acha.2012.08.007http://dx.doi.org/10.1016/j.acha.2012.08.007 CrossRefGoogle Scholar
[9] Han, B., Symmetric tight framelet filter banks with three high-pass filters. Preprint.Google Scholar
[10] Han, B. and Mo, Q., Tight wavelet frames generated by three symmetric B-spline functions with high vanishing moments. Proc. Amer. Math. Soc. 132 (2003, 77–86.http://dx.doi.org/10.1090/S0002-9939-03-07205-8 Google Scholar
[11] Han, B. and Mo, Q., Splitting a matrix of Laurent polynomials with symmetry and its applications to symmetric framelet filter banks. SIAM J. Matrix Anal. Appl. 26 (2004, 97–124. http://dx.doi.org/10.1137/S0895479802418859 Google Scholar
[12] Han, B. and Mo, Q., Symmetric MRA tight wavelet frames with three generators and high vanishing moments. Appl. Comput. Harmon. Anal. 18 (2005. 67–93.http://dx.doi.org/10.1016/j.acha.2004.09.001 CrossRefGoogle Scholar
[13] Han, B. and Mo, Q., Dilations and completions for Gabor systems. J. Fourier Anal. Appl. 15 (2009, 201–217.http://dx.doi.org/10.1007/s00041-008-9028-y CrossRefGoogle Scholar
[14] Jeong, B., Choi, M., and Kim, H. O., Construction of symmetric tight wavelet frames from quasi-interpolatory subdivision masks and their applications. Int. J.Wavelets Multiresolut. Inf. Process. 6 (2008, 97–120.http://dx.doi.org/10.1142/S0219691308002240 CrossRefGoogle Scholar
[15] Jiang, Q. T., Parametrizations of masks for tight affine frames with two symmetric/antisymmetric generators. Adv. Comput. Math. 18 (2003, 247–268.http://dx.doi.org/10.1023/A:1021339707805 CrossRefGoogle Scholar
[16] Li, D. F. and Sun, W., Expansion of frames to tight frames. Acta. Math. Sin. (Engl. Ser.) 25 (2009, 287–292.http://dx.doi.org/10.1007/s10114-008-6577-6 CrossRefGoogle Scholar
[17] Petukhov, A., Symmetric framelets. Constr. Approx. 19 (2003, 309–328.http://dx.doi.org/10.1007/s00365-002-0522-1 CrossRefGoogle Scholar
[18] Ron, A. and Shen, Z., Frames and stable bases for shift-invariant subspaces of L2(Rd). Canad. J. Math. 47 (1995, 1051–1094.http://dx.doi.org/10.4153/CJM-1995-056-1 CrossRefGoogle Scholar
[19] Ron, A. and Shen, Z., Affine systems in L2(Rd): The analysis of the analysis operator. J. Funct. Anal. 148 (1997, 408–447.http://dx.doi.org/10.1006/jfan.1996.3079 CrossRefGoogle Scholar
[20] Ron, A. and Shen, Z., Affine systems in L2(Rd) II: dual systems. J. Fourier Anal. Appl. 3 (1997, 617–637.http://dx.doi.org/10.1007/BF02648888 CrossRefGoogle Scholar
[21] Selesnick, I.W. and Abdelnour, A. F., Symmetric wavelet tight frames with two generators. Appl. Comput. Harmon. Anal. 17 (2004, 211–225.http://dx.doi.org/10.1016/j.acha.2004.05.003 CrossRefGoogle Scholar