Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T16:52:56.505Z Has data issue: false hasContentIssue false
  • English
  • Français

A Homological Property and Arens Regularity of Locally Compact Quantum Groups

Published online by Cambridge University Press:  20 November 2018

Mohammad Reza Ghanei ,
Rasoul Nasr-Isfahani  and
Mehdi Nemati
Mohammad Reza Ghanei
Affiliation:
Department of Mathematics, Khansar Faculty of Mathematics and Computer Science, Khansar, Iran e-mail: mr.ghanei@math.iut.ac.ir
Rasoul Nasr-Isfahani
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395–5746, Iran Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran e-mail: isfahani@cc.iut.ac.ir e-mail: m.nemati@cc.iut.ac.ir
Mehdi Nemati
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395–5746, Iran Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran e-mail: isfahani@cc.iut.ac.ir e-mail: m.nemati@cc.iut.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize two important notions of amenability and compactness of a locally compact quantum group 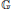$\mathbb{G}$ in terms of certain homological properties. For this, we show that 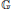$\mathbb{G}$ is character amenable if and only if it is both amenable and co-amenable. We finally apply our results to Arens regularity problems of the quantum group algebra 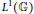${{L}^{1}}\left( \mathbb{G} \right)$. In particular, we improve an interesting result by Hu, Neufang, and Ruan.

Keywords

46L8943A0746H2046M1058B32amenabilityArens regularityco-amenabilitylocally compact quantum grouphomological property
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 122 - 130
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Aristov, O. Y., Amenability and compact type for Hopf-von Neumann algebras from the homological point of view. In: Banach algebras and their applications. Contemporary Mathematics 363. American Mathematical Society, Providence, RI, 200, pp. 15–37. http://dx.doi.Org/10.1090/conm/363/06638 Google Scholar
[2] Bédos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003) 865–884. http://dx.doi.Org/10.1142/S01 291 67X03002046 Google Scholar
[3] Desmedt, P., Quaegebeur, J., and Vaes, S., Amenability and the bicrossed product construction. Illinois J. Math. 46(2002), 1259–1277.Google Scholar
[4] Forrest, B., Arens regularity and discrete groups. Pacific J. Math. 151(1991), 217–227. http://dx.doi.Org/10.2140/pjm.1991.151.217 Google Scholar
[5] Hu, Z., Neufang, M., and Ruan, Z. J., On topological centre problems and SIN quantum groups. J. Funct. Anal. 257(2009), 610–640. http://dx.doi.Org/10.1016/j.jfa.2009.02.004 Google Scholar
[6] Hu, Z., Neufang, M., and Ruan, Z. J., Module maps over locally compact quantum groups. Studia Math. 211(2012), 111–145 http://dx.doi.Org/10.4064/sm211-2-2 Google Scholar
[7] Kalantar, M. and Neufang, M., From quantum groups to groups. Canadian J. Math. 65(2013), 1073–1094. http://dx.doi.Org/10.4153/CJM-2012-047-X Google Scholar
[8] Kaniuth, E., Lau, A. T., and Pym, J., On f-amenability ofBanach algebras. Math. Proc. Cambridge Philos. Soc. 144(2008), 85–96. http://dx.doi.Org/10.101 7/S0305004107000874 Google Scholar
[9] Kaniuth, E., Lau, A. T., and Pym, J., On character amenability ofBanach algebras. J. Math. Anal. Appl. 344(2008), 942–955. http://dx.doi.Org/10.1016/j.jmaa.2008.03.037 Google Scholar
[10] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Scient. Ec. Norm. Sup. 33(2000), 837–934. http://dx.doi.Org/10.1016/S0012-9593(00)01055-7 Google Scholar
[11] Kustermans, J. and Vaes, S., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), 68–92.Google Scholar
[12] Lau, A. T., Analysis on a class ofBanach algebras with application to harmonic analysis on locally compact groups and semigroups. Fund. Math. 118(1983), 161–175.Google Scholar
[13] Monfared, M. S., Character amenability ofBanach algebras. Math. Proc. Cambridge Philos. Soc. 144(2008), 697–706. http://dx.doi.Org/10.1017/S0305004108001126 Google Scholar
[14] Rudin, W., Functional analysis. McGraw-Hill, New York, 1973.Google Scholar
[15] Runde, V., Characterizations of compact and discrete quantum groups through second duals. J. Operator Theory 60(2008), 415–428.Google Scholar
[16] Runde, V., Uniform continuity over locally compact quantum groups. J. London Math. Soc. 80(2009), 55–71. http://dx.doi.Org/10.1112/jlms/jdpO11 Google Scholar
[17] Sahami, A. and Pourabbas, A., On f-biflat and f-biprojective Banach algebras. Bull. Belg. Math. Soc. Simon Stevin 20(2013), 789–801.Google Scholar
[18] Soltan, P. and Viselter, A., A note on amenability of locally compact quantum groups. Canad. Math. Bull. 57(2014), 424–430. http://dx.doi.Org/10.41 53/CMB-2O12-032-3 Google Scholar
[19] Tomatsu, R., Amenable discrete quantum groups. J. Math. Soc. Japan. 58(2006), 949–964. http://dx.doi.Org/10.2969/jmsj71179759531 Google Scholar
[20] Ülger, A., Arens regularity of the weakly sequentially complete Banach algebras and applications. Proc. Amer. Math. Soc. 127(1999), 3221–3227. http://dx.doi.Org/! 0.1090/S0002-9939-99-04894-7 Google Scholar