Article contents
Symplectic Degenerate Flag Varieties
Published online by Cambridge University Press: 20 November 2018
Abstract
A simple finite dimensional module 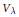 ${{V}_{\lambda }}$ of a simple complex algebraic group
${{V}_{\lambda }}$ of a simple complex algebraic group 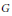 $G$ is naturally endowed with a filtration induced by the PBW-filtration of
$G$ is naturally endowed with a filtration induced by the PBW-filtration of 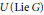 $U\,(\text{Lie}\,G)$. The associated graded space
$U\,(\text{Lie}\,G)$. The associated graded space 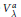 $\text{V}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$ is a module for the group
$\text{V}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$ is a module for the group 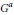 ${{G}^{a}}$, which can be roughly described as a semi-direct product of a Borel subgroup of
${{G}^{a}}$, which can be roughly described as a semi-direct product of a Borel subgroup of 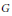 $G$ and a large commutative unipotent group
$G$ and a large commutative unipotent group 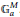 $\mathbb{G}_{a}^{M}$. In analogy to the flag variety
$\mathbb{G}_{a}^{M}$. In analogy to the flag variety 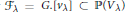 ${{\mathcal{F}}_{\lambda }}\,=\,G.[{{v}_{\lambda }}]\,\,\subset \,\,\mathbb{P}({{V}_{\lambda }})$, we call the closure
${{\mathcal{F}}_{\lambda }}\,=\,G.[{{v}_{\lambda }}]\,\,\subset \,\,\mathbb{P}({{V}_{\lambda }})$, we call the closure 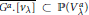 $\overline{{{G}^{a}}\,.\,[{{v}_{\text{ }\!\!\lambda\!\!\text{ }}}]}\,\,\subset \,\,\mathbb{P}\,(V_{\text{ }\!\!\lambda\!\!\text{ }}^{a})$ of the
$\overline{{{G}^{a}}\,.\,[{{v}_{\text{ }\!\!\lambda\!\!\text{ }}}]}\,\,\subset \,\,\mathbb{P}\,(V_{\text{ }\!\!\lambda\!\!\text{ }}^{a})$ of the 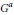 ${{G}^{a}}$-orbit through the highest weight line the degenerate flag variety
${{G}^{a}}$-orbit through the highest weight line the degenerate flag variety 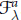 $\mathcal{F}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$. In general this is a singular variety, but we conjecture that it has many nice properties similar to that of Schubert varieties. In this paper we consider the case of
$\mathcal{F}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$. In general this is a singular variety, but we conjecture that it has many nice properties similar to that of Schubert varieties. In this paper we consider the case of 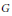 $G$ being the symplectic group. The symplectic case is important for the conjecture because it is the first known case where, even for fundamental weights
$G$ being the symplectic group. The symplectic case is important for the conjecture because it is the first known case where, even for fundamental weights 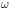 $\omega$, the varieties
$\omega$, the varieties 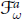 $\mathcal{F}_{\text{ }\!\!\omega\!\!\text{ }}^{a}$ differ from
$\mathcal{F}_{\text{ }\!\!\omega\!\!\text{ }}^{a}$ differ from  ${{\mathcal{F}}_{\text{ }\!\!\omega\!\!\text{ }}}$. We give an explicit construction of the varieties
${{\mathcal{F}}_{\text{ }\!\!\omega\!\!\text{ }}}$. We give an explicit construction of the varieties 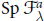 $\text{Sp}\,\mathcal{F}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$ and construct desingularizations, similar to the Bott–Samelson resolutions in the classical case. We prove that
$\text{Sp}\,\mathcal{F}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$ and construct desingularizations, similar to the Bott–Samelson resolutions in the classical case. We prove that 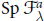 $\text{Sp}\,\mathcal{F}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$ are normal locally complete intersections with terminal and rational singularities. We also show that these varieties are Frobenius split. Using the above mentioned results, we prove an analogue of the Borel–Weil theorem and obtain a
$\text{Sp}\,\mathcal{F}_{\text{ }\!\!\lambda\!\!\text{ }}^{a}$ are normal locally complete intersections with terminal and rational singularities. We also show that these varieties are Frobenius split. Using the above mentioned results, we prove an analogue of the Borel–Weil theorem and obtain a 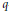 $q$-character formula for the characters of irreducible
$q$-character formula for the characters of irreducible 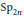 $\text{S}{{\text{p}}_{2\pi }}$-modules via the Atiyah–Bott–Lefschetz fixed points formula.
$\text{S}{{\text{p}}_{2\pi }}$-modules via the Atiyah–Bott–Lefschetz fixed points formula.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
- 16
- Cited by


