Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T08:17:59.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Subregular Nilpotent Elements and Bases in 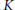$K$-Theory

Published online by Cambridge University Press:  20 November 2018

G. Lusztig
G. Lusztig*
Affiliation:
Department of Mathematics, M. I. T., Cambridge, Massachusetts 02139, U.S.A. Institute for Advanced Study, Princeton, New Jersey 08540, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we describe a canonical basis for the equivariant 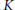$K$-theory (with respect to a ${{\mathbf{C}}^{*}}$-action) of the variety of Borel subalgebras containing a subregular nilpotent element of a simple complex Lie algebra of type 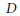$D$ or 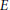$E$.

Keywords

20G99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 6 , 01 December 1999 , pp. 1194 - 1225
Copyright
Copyright © Canadian Mathematical Society 1999

References

[B] Brieskorn, E., Singular elements of semisimple algebraic groups, Actes Congrès Intern. Math. 2(1970), 279–284.Google Scholar
[C] Coxeter, H. S. M., The product of generators of a finite group generated by reflections, Duke Math. J. 18(1951), 765–782.Google Scholar
[GV] Gonzales-Sprinberg, G. and Verdier, J.-L., Construction géométrique de la correspondance de McKay, Ann. Sci. École Norm. Sup. 16(1983), 409–449.Google Scholar
[IN] Ito, Y. and Nakamura, I., McKay correspondence and Hilbert schemes. Proc. Japan Acad. Ser. A Math. Sci. 72(1996), 135–138.Google Scholar
[KL] Kazhdan, D. and Lusztig, G., Proof of the Deligne-Langlands conjecture for Hecke algebras. Invent. Math. 53(1979), 153–215.Google Scholar
[Kr] Kronheimer, P. B., The construction of ALE spaces as hyper-Kähler quotients. J. Differential Geom. 29(1989), 665–683.Google Scholar
[L1] Lusztig, G., Some examples of square integrable representations of semisimple p-adic groups. Trans. Amer. Math. Soc. 277(1983), 623–653.Google Scholar
[L2] Lusztig, G., Quivers, perverse sheaves and quantized enveloping algebras. J. Amer.Math. Soc. 4(1991), 365–421.Google Scholar
[L3] Lusztig, G., On quiver varieties. Adv. inMath. 136(1988), 141–182.Google Scholar
[L4] Lusztig, G., Bases in equivariant K-theory. Represent. Th. (electronic) 2(1998), 298–369.Google Scholar
[L5] Lusztig, G., Bases in equivariant K-theory, II. Represent. Th. (electronic) 3(1999), 281–353.Google Scholar
[M] McKay, J., Graphs, singularities and finite groups. Proc. Sympos. Pure Math. 37(1980), 183–186.Google Scholar
[N1] Nakajima, H., Instantons on ALE spaces, quiver varieties and Kac-Moody algebras. DukeMath. J. 76(1994), 365–416.Google Scholar
[N2] Nakajima, H., Lectures on Hilbert schemes of points on surfaces. (1996).Google Scholar
[S] Slodowy, P. Simple algebraic groups and simple singularities. Lecture Notes in Math. 815, Springer Verlag, Berlin, Heidelberg, New York, 1980.Google Scholar