Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T06:43:47.902Z Has data issue: false hasContentIssue false
  • English
  • Français

A Construction of Rigid Analytic Cohomology Classes for Congruence Subgroups of SL3(ℤ)

Published online by Cambridge University Press:  20 November 2018

David Pollack  and
Robert Pollack
David Pollack
Affiliation:
Department of Mathematics & Statistics, Boston University, 111 Cummington Street, Boston, MA 02215, USA, rpollack@math.bu.edu
Robert Pollack
Affiliation:
Department of Mathematics & Computer Science, Wesleyan University, Science Tower 655, Middletown, CT 06459, USA, dpollack@wesleyan.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a constructive proof, in the special case of 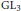$\text{G}{{\text{L}}_{3}}$, of a theorem of Ash and Stevens which compares overconvergent cohomology to classical cohomology. Namely, we show that every ordinary classical Hecke-eigenclass can be lifted uniquely to a rigid analytic eigenclass. Our basic method builds on the ideas of M. Greenberg; we first form an arbitrary lift of the classical eigenclass to a distribution-valued cochain. Then, by appropriately iterating the 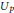${{U}_{p}}$-operator, we produce a cocycle whose image in cohomology is the desired eigenclass. The constructive nature of this proof makes it possible to perform computer computations to approximate these interesting overconvergent eigenclasses.

Keywords

11F7511F85
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 674 - 690
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Ash, A., Cohomology of congruence subgroups SL(n, Z). Math. Ann). 249(1980), no. 1, 55–73.Google Scholar
[2] Ash, A., Pollack, D., and Stevens, G., Rigidity of p-adic cohomology classes of congruence subgroups of GL(n, Z). Proc. London. Math. Soc. 96(2008), no. 2, 367–388.Google Scholar
[3] Ash, A., Doud, D., and Pollack, D., Galois representations with conjectural connections to arithmetic cohomology. Duke Math. J.112(2002), no. 3, 521–579.Google Scholar
[4] Ash, A., Grayson, D., and Green, P., Computations of cuspidal cohomology of congruence subgroups of SL(3, Z). J. Number Theor). 19(1984), no. 3, 412–436.Google Scholar
[5] Ash, A., Stevens, G., p-adic deformations of cohomology classes of subgroups of GL(n, Z). Journèes Arithmètiques, (Barcelona, 1995) Collect. Math). 48(1997), no. 1-2, 1–30.Google Scholar
[6] Ash, A. and Stevens, G., p-adic deformations of cohomology on GL(n): the non-ordinary case. In preparation, draft available at http://math.bu.edu/people/ghs/research.d.Google Scholar
[7] Darmon, H., Integration onHp ×Hand arithmetic applications. Ann. of Math. 154(2001), no. 3, 589–639.Google Scholar
[8] Darmon, H. and Pollack, R., The efficient calculation of Stark-Heegner points via overconvergent modular symbols. Israel J. Math. 153(2006), 319–354.Google Scholar
[9] Greenberg, M., Lifting modular symbols of non-critical slope. Israel J. Math. 161(2007), 141–155.Google Scholar
[10] Pollack, R. and Stevens, G., Overconvergent modular symbols and p-adic L-functions. Preprint, available at http://math.bu.edu/people/rpollack/Papers.Google Scholar
[11] Pollack, R. and Stevens, G., Critical slope p-adic L-functions. In preparation, draft available at http://math.bu.edu/people/rpollack/Papers. 12] Stevens, G., Rigid Analytic Modular Symbols. Preprint, available at http://math.bu.edu/people/ghs/research.d.Google Scholar
[13] Trifković, M., Stark-Heegner points on elliptic curves defined over imaginary quadratic fields. Duke Math. J. 135(2006), no. 3, 415–453.Google Scholar