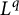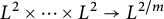1 Introduction and preliminaries
The pointwise a.e. convergence of sequences of operators is of paramount importance and has been widely studied in several areas of analysis, such as harmonic analysis, PDE, and ergodic theory. This area boasts challenging problems (indicatively see [Reference Carbery, Rubio de Francia and Vega5, Reference Carleson6, Reference Du, Guth and Li12, Reference Jessen, Marcinkiewicz and Zygmund24]), and is intimately connected with the boundedness of the associated maximal operators; on this, see [Reference Stein27]. Moreover, techniques and tools employed to study a.e. convergence have led to important developments in harmonic analysis.
Multilinear harmonic analysis has made significant advances in recent years. The founders of this area are Coifman and Meyer [Reference Coifman and Meyer8], who realized the applicability of multilinear operators and introduced their study in analysis in the mid-1970s. Focusing on operators that commute with translations, a fundamental difference between the multilinear theory and the linear theory is the existence of a straightforward characterization of boundedness at an initial point, usually
![]() $L^2\to L^2$
. The lack of an easy characterization of boundedness at an initial point in the multilinear theory creates difficulties in their study. Criteria that get very close to characterization of boundedness have recently been obtained by the first two authors and Slavíková [Reference Grafakos, He and Slavíková19] and by Kato, Miyachi, and Tomita [Reference Kato, Miyachi and Tomita25] in the bilinear case. These criteria were extended to the general m-linear case for
$L^2\to L^2$
. The lack of an easy characterization of boundedness at an initial point in the multilinear theory creates difficulties in their study. Criteria that get very close to characterization of boundedness have recently been obtained by the first two authors and Slavíková [Reference Grafakos, He and Slavíková19] and by Kato, Miyachi, and Tomita [Reference Kato, Miyachi and Tomita25] in the bilinear case. These criteria were extended to the general m-linear case for
![]() $m\ge 2$
by the authors of this article in [Reference Grafakos, He, Honzík and Park18]. This reference also contains initial
$m\ge 2$
by the authors of this article in [Reference Grafakos, He, Honzík and Park18]. This reference also contains initial
![]() $L^2\times \cdots \times L^2\to L^{2/m}$
estimates for rough homogeneous multilinear singular integrals associated with
$L^2\times \cdots \times L^2\to L^{2/m}$
estimates for rough homogeneous multilinear singular integrals associated with
![]() $L^q$
functions on the sphere and multilinear multipliers of Hörmander type.
$L^q$
functions on the sphere and multilinear multipliers of Hörmander type.
The purpose of this work is to obtain the pointwise a.e. convergence of doubly truncated multilinear homogeneous singular integrals and lacunary multilinear multipliers by establishing boundedness for their associated maximal operators.
We first introduce multilinear (singly) truncated singular integral operators. Let
![]() $\Omega $
be an integrable function, defined on the sphere
$\Omega $
be an integrable function, defined on the sphere
![]() $\mathbb {S}^{mn-1}$
, satisfying the mean value zero property
$\mathbb {S}^{mn-1}$
, satisfying the mean value zero property
Then we define
 $$ \begin{align*} K(\vec{{y}}\,):=\frac{\Omega(\vec{{y}}\,')}{|\vec{{y}}\,|^{mn}}, \qquad \vec y \neq 0, \end{align*} $$
$$ \begin{align*} K(\vec{{y}}\,):=\frac{\Omega(\vec{{y}}\,')}{|\vec{{y}}\,|^{mn}}, \qquad \vec y \neq 0, \end{align*} $$
where
![]() $\vec {{y}}\,':=\vec {{y}}\,/|\vec {{y}}\,|\in \mathbb {S}^{mn-1}$
, and the corresponding truncated multilinear operator
$\vec {{y}}\,':=\vec {{y}}\,/|\vec {{y}}\,|\in \mathbb {S}^{mn-1}$
, and the corresponding truncated multilinear operator
![]() ${\mathcal {L}}_{\Omega }^{(\epsilon )}$
by
${\mathcal {L}}_{\Omega }^{(\epsilon )}$
by
 $$ \begin{align*}\mathcal L^{(\epsilon)}_{\Omega}\big(f_1,\dots,f_m\big)(x):=\int_{(\mathbb R^n)^m\setminus B(0,\epsilon)}{K(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \end{align*} $$
$$ \begin{align*}\mathcal L^{(\epsilon)}_{\Omega}\big(f_1,\dots,f_m\big)(x):=\int_{(\mathbb R^n)^m\setminus B(0,\epsilon)}{K(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \end{align*} $$
acting on Schwartz functions
![]() $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
![]() $\mathbb R^n$
, where
$\mathbb R^n$
, where
![]() $x\in \mathbb R^n$
,
$x\in \mathbb R^n$
,
![]() $\vec {{y}}\,:=(y_1,\dots ,y_m)\in (\mathbb R^n)^m$
, and
$\vec {{y}}\,:=(y_1,\dots ,y_m)\in (\mathbb R^n)^m$
, and
![]() $B(0,\epsilon )$
, is the ball centered at zero with radius
$B(0,\epsilon )$
, is the ball centered at zero with radius
![]() $\epsilon>0$
in
$\epsilon>0$
in
![]() $(\mathbb R^n)^m$
. Moreover, by taking
$(\mathbb R^n)^m$
. Moreover, by taking
![]() $\epsilon \searrow 0$
, we obtain the multilinear homogeneous Calderón–Zygmund singular integral operator
$\epsilon \searrow 0$
, we obtain the multilinear homogeneous Calderón–Zygmund singular integral operator
 $$ \begin{align} \mathcal L_{\Omega}\big(f_1,\dots,f_m\big)(x)&:=\lim_{\epsilon\searrow 0}\mathcal L^{(\epsilon)}_{\Omega}\big(f_1,\dots,f_m\big)(x) \\ &=p.v. \int_{(\mathbb R^n)^m}{K(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\,. \nonumber \end{align} $$
$$ \begin{align} \mathcal L_{\Omega}\big(f_1,\dots,f_m\big)(x)&:=\lim_{\epsilon\searrow 0}\mathcal L^{(\epsilon)}_{\Omega}\big(f_1,\dots,f_m\big)(x) \\ &=p.v. \int_{(\mathbb R^n)^m}{K(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\,. \nonumber \end{align} $$
This is still well defined for any Schwartz functions
![]() $f_1, \dots ,f_m$
on
$f_1, \dots ,f_m$
on
![]() $\mathbb R^n$
. In [Reference Grafakos, He, Honzík and Park18], we showed that if
$\mathbb R^n$
. In [Reference Grafakos, He, Honzík and Park18], we showed that if
![]() $\Omega $
lies in
$\Omega $
lies in
![]() $ L^q (\mathbb {S}^{mn-1}) $
with
$ L^q (\mathbb {S}^{mn-1}) $
with
![]() $q>\frac {2m}{m+1}$
, then the multilinear singular integral operator
$q>\frac {2m}{m+1}$
, then the multilinear singular integral operator
![]() ${\mathcal {L}}_{\Omega }$
admits a bounded extension from
${\mathcal {L}}_{\Omega }$
admits a bounded extension from
![]() $L^2(\mathbb R^n)\times \cdots \times L^2(\mathbb R^n)$
to
$L^2(\mathbb R^n)\times \cdots \times L^2(\mathbb R^n)$
to
![]() $L^{2/m}(\mathbb R^n)$
. In order words, given
$L^{2/m}(\mathbb R^n)$
. In order words, given
![]() $f_j\in L^2(\mathbb R^n)$
,
$f_j\in L^2(\mathbb R^n)$
,
![]() ${\mathcal {L}}_{\Omega }(f_1,\dots ,f_m)$
is well defined and is in
${\mathcal {L}}_{\Omega }(f_1,\dots ,f_m)$
is well defined and is in
![]() $L^{2/m}(\mathbb R^n)$
.
$L^{2/m}(\mathbb R^n)$
.
We now define the doubly truncated multilinear operator
![]() ${\mathcal {L}}_{\Omega }^{(\epsilon ,\epsilon ^{-1})}$
by
${\mathcal {L}}_{\Omega }^{(\epsilon ,\epsilon ^{-1})}$
by
for Schwartz functions
![]() $f_j$
,
$f_j$
,
![]() $j=1,\dots ,m$
. We observe that if
$j=1,\dots ,m$
. We observe that if
![]() $\Omega \in L^q(\mathbb {S}^{mn-1})$
for
$\Omega \in L^q(\mathbb {S}^{mn-1})$
for
![]() $\frac {2m}{m+1}<q\le \infty $
, then
$\frac {2m}{m+1}<q\le \infty $
, then
for
![]() $f_j$
in the Schwartz class.
$f_j$
in the Schwartz class.
We define, for fixed
![]() $0<\epsilon _0<1$
,
$0<\epsilon _0<1$
,
and
for
![]() $\varphi _j$
in the Schwartz class. One main difficulty to study the boundedness of
$\varphi _j$
in the Schwartz class. One main difficulty to study the boundedness of
![]() $\mathcal L^{**}_{\Omega }$
is to show that the doubly truncated operator is well defined pointwise a.e. for
$\mathcal L^{**}_{\Omega }$
is to show that the doubly truncated operator is well defined pointwise a.e. for
![]() $f_j\in L^2(\mathbb {R}^n)$
. To overcome this difficulty, we need to utilize the boundedness of
$f_j\in L^2(\mathbb {R}^n)$
. To overcome this difficulty, we need to utilize the boundedness of
![]() $\mathcal M_{\Omega }$
introduced in Section 3 (see Section 5 for the detailed proof).
$\mathcal M_{\Omega }$
introduced in Section 3 (see Section 5 for the detailed proof).
Our first main result is as follows.
Theorem 1.1 Let
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $\frac {2m}{m+1}<q\le \infty $
, and
$\frac {2m}{m+1}<q\le \infty $
, and
![]() $\Omega \in L^q (\mathbb S^{mn-1})$
satisfy (1.1). Then
$\Omega \in L^q (\mathbb S^{mn-1})$
satisfy (1.1). Then
 $$ \begin{align} \big\|{\mathcal{L}}_{\Omega}^{** }(f_1,\dots , f_m)\big\|_{L^{2/m}(\mathbb{R}^n) } \le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})} \prod_{j=1}^{\infty}\| f_j\|_{L^{2}(\mathbb{R}^n)} \end{align} $$
$$ \begin{align} \big\|{\mathcal{L}}_{\Omega}^{** }(f_1,\dots , f_m)\big\|_{L^{2/m}(\mathbb{R}^n) } \le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})} \prod_{j=1}^{\infty}\| f_j\|_{L^{2}(\mathbb{R}^n)} \end{align} $$
for
![]() $f_j\in L^2(\mathbb {R}^n)$
. Moreover, the doubly truncated singular integral
$f_j\in L^2(\mathbb {R}^n)$
. Moreover, the doubly truncated singular integral
![]() ${\mathcal {L}}_{\Omega }^{(\epsilon ,\epsilon ^{-1})}(f_1,\dots , f_m)$
converges to
${\mathcal {L}}_{\Omega }^{(\epsilon ,\epsilon ^{-1})}(f_1,\dots , f_m)$
converges to
![]() ${\mathcal {L}}_{\Omega }(f_1,\dots ,f_m)$
pointwise a.e. as
${\mathcal {L}}_{\Omega }(f_1,\dots ,f_m)$
pointwise a.e. as
![]() $\epsilon \to 0$
when
$\epsilon \to 0$
when
![]() $f_j\in L^2(\mathbb {R}^n)$
,
$f_j\in L^2(\mathbb {R}^n)$
,
![]() $j=1,\dots , m$
. That is, the multilinear singular integral
$j=1,\dots , m$
. That is, the multilinear singular integral
![]() ${\mathcal {L}}_{\Omega }(f_1,\dots ,f_m)$
is well defined a.e. when
${\mathcal {L}}_{\Omega }(f_1,\dots ,f_m)$
is well defined a.e. when
![]() $f_j\in L^2(\mathbb {R}^n)$
,
$f_j\in L^2(\mathbb {R}^n)$
,
![]() $j=1,\dots , m$
.
$j=1,\dots , m$
.
In order to achieve this goal, we initially prove the following result, which provides the boundedness of the associated maximal singular integral operator:
for Schwartz functions
![]() $f_j$
,
$f_j$
,
![]() $j=1,\dots ,m$
.
$j=1,\dots ,m$
.
Theorem 1.2 Let
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $\frac {2m}{m+1}<q\le \infty $
, and
$\frac {2m}{m+1}<q\le \infty $
, and
![]() $\Omega \in L^q (\mathbb S^{mn-1})$
satisfy (1.1). Then there exists a constant
$\Omega \in L^q (\mathbb S^{mn-1})$
satisfy (1.1). Then there exists a constant
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align} \big\Vert {\mathcal{L}}_{\Omega}^*(f_1,\dots,f_m)\big\Vert_{L^{2/m}(\mathbb R^n)}\le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2(\mathbb R^n)} \end{align} $$
$$ \begin{align} \big\Vert {\mathcal{L}}_{\Omega}^*(f_1,\dots,f_m)\big\Vert_{L^{2/m}(\mathbb R^n)}\le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2(\mathbb R^n)} \end{align} $$
for Schwartz functions
![]() $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
This extends and improves a result obtained in [Reference Buriánková and Honzík3] which treated the case
![]() $m=2$
and
$m=2$
and
![]() $q=\infty $
. Theorem 1.2 follows from Propositions 4.1 and 4.2, which are counterparts of Propositions 5 and 4 in [Reference Buriánková and Honzík3], respectively. We improve the two propositions in the m-linear settings. Remark that the assumption
$q=\infty $
. Theorem 1.2 follows from Propositions 4.1 and 4.2, which are counterparts of Propositions 5 and 4 in [Reference Buriánková and Honzík3], respectively. We improve the two propositions in the m-linear settings. Remark that the assumption
![]() $\Omega \in L^2(\mathbb {S}^{2n-1})$
in Proposition 5 and Theorem 2 in [Reference Buriánková and Honzík3] should be
$\Omega \in L^2(\mathbb {S}^{2n-1})$
in Proposition 5 and Theorem 2 in [Reference Buriánková and Honzík3] should be
![]() $\Omega \in L^{\infty }(\mathbb {S}^{2n-1})$
. One of the main improvements is the
$\Omega \in L^{\infty }(\mathbb {S}^{2n-1})$
. One of the main improvements is the
![]() $L^{p_1}\times \cdots \times L^{p_m}\to L^p$
estimate for
$L^{p_1}\times \cdots \times L^{p_m}\to L^p$
estimate for
![]() $\mathfrak {T}_K^{**}$
in (4.10) with a bound
$\mathfrak {T}_K^{**}$
in (4.10) with a bound
![]() $\Vert \Omega \Vert _{L^1(\mathbb {S}^{mn-1})}$
, while a simple m-linear extension of the arguments in [Reference Buriánková and Honzík3] requires the bound
$\Vert \Omega \Vert _{L^1(\mathbb {S}^{mn-1})}$
, while a simple m-linear extension of the arguments in [Reference Buriánková and Honzík3] requires the bound
![]() $\Vert \Omega \Vert _{L^{\infty }(\mathbb {S}^{mn-1})}$
for the estimate, which originated simply from the kernel estimate
$\Vert \Omega \Vert _{L^{\infty }(\mathbb {S}^{mn-1})}$
for the estimate, which originated simply from the kernel estimate
where
![]() $\mathfrak {T}_K^{**}$
is defined in (4.6) and its kernel
$\mathfrak {T}_K^{**}$
is defined in (4.6) and its kernel
![]() $K_{\tau }^{**}$
is in (4.7). For the improvement, we incorporate a delicate decomposition, as we are unable to use the kernel estimate (1.6) (see (4.8)). To obtain the results in Proposition 4.2, we suitably combine Littlewood–Paley techniques and wavelet decompositions to reduce the boundedness of
$K_{\tau }^{**}$
is in (4.7). For the improvement, we incorporate a delicate decomposition, as we are unable to use the kernel estimate (1.6) (see (4.8)). To obtain the results in Proposition 4.2, we suitably combine Littlewood–Paley techniques and wavelet decompositions to reduce the boundedness of
![]() ${\mathcal {L}}_{\Omega ,\mu }^{\sharp }$
to estimates for norms of maximal operators associated with lattice bumps with suitable decay. This is the essential contribution of this article in view of the fact that the bilinear argument in [Reference Buriánková and Honzík3, Proposition 4] does not apply due to the complicated structure of general m-linear operators for
${\mathcal {L}}_{\Omega ,\mu }^{\sharp }$
to estimates for norms of maximal operators associated with lattice bumps with suitable decay. This is the essential contribution of this article in view of the fact that the bilinear argument in [Reference Buriánková and Honzík3, Proposition 4] does not apply due to the complicated structure of general m-linear operators for
![]() $m\ge 3$
(see (4.14) for the exact formulation). This result is actually proved in terms of Plancherel-type inequalities, recently developed in [Reference Grafakos, He, Honzík and Park18] and stated in Proposition 2.1.
$m\ge 3$
(see (4.14) for the exact formulation). This result is actually proved in terms of Plancherel-type inequalities, recently developed in [Reference Grafakos, He, Honzík and Park18] and stated in Proposition 2.1.
The tools used to establish Theorem 1.1 turn out to be useful in the study of pointwise convergence problems of several related operators. As an example, let us take multilinear multipliers with limited decay to demonstrate our idea.
For a smooth function
![]() $\sigma \in \mathscr {C}^{\infty }((\mathbb R^n)^m)$
and
$\sigma \in \mathscr {C}^{\infty }((\mathbb R^n)^m)$
and
![]() $\nu \in \mathbb {Z}$
, let
$\nu \in \mathbb {Z}$
, let
 $$ \begin{align} S_{\sigma}^{\nu}\big(f_1,\dots,f_m\big)(x):=\int_{(\mathbb R^n)^m}{\sigma(2^{\nu}\vec{{\xi}}\,)\bigg( \prod_{j=1}^{m}\widehat{f_j}(\xi_j)\bigg)e^{2\pi i\langle x,\sum_{j=1}^{m}\xi_j \rangle}} ~d\,\vec{{\xi}}\, \end{align} $$
$$ \begin{align} S_{\sigma}^{\nu}\big(f_1,\dots,f_m\big)(x):=\int_{(\mathbb R^n)^m}{\sigma(2^{\nu}\vec{{\xi}}\,)\bigg( \prod_{j=1}^{m}\widehat{f_j}(\xi_j)\bigg)e^{2\pi i\langle x,\sum_{j=1}^{m}\xi_j \rangle}} ~d\,\vec{{\xi}}\, \end{align} $$
for Schwartz functions
![]() $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
![]() $\mathbb R^n$
, where
$\mathbb R^n$
, where
![]() $\vec {{\xi }}\,:=(\xi _1,\dots ,\xi _m) \in (\mathbb R^n)^m$
.
$\vec {{\xi }}\,:=(\xi _1,\dots ,\xi _m) \in (\mathbb R^n)^m$
.
We are interested in the pointwise convergence of
![]() $S^{\nu }_{\sigma }$
when
$S^{\nu }_{\sigma }$
when
![]() $\nu \to -\infty $
. We pay particular attention to
$\nu \to -\infty $
. We pay particular attention to
![]() $\sigma $
satisfying the limited decay property (for some fixed a)
$\sigma $
satisfying the limited decay property (for some fixed a)
for sufficiently many
![]() $\beta $
. Examples of multipliers of this type include
$\beta $
. Examples of multipliers of this type include
![]() $\widehat \mu $
, the Fourier transform of the spherical measure
$\widehat \mu $
, the Fourier transform of the spherical measure
![]() $\mu $
(see [Reference Calderón4, Reference Coifman and Weiss7, Reference Rubio de Francia26] for the corresponding linear results).
$\mu $
(see [Reference Calderón4, Reference Coifman and Weiss7, Reference Rubio de Francia26] for the corresponding linear results).
The second contribution of this work is the following result.
Theorem 1.3 Let
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $a>\frac {(m-1)n}{2}$
. Let
$a>\frac {(m-1)n}{2}$
. Let
![]() $\sigma \in \mathscr {C}^{\infty }((\mathbb R^n)^m)$
satisfy
$\sigma \in \mathscr {C}^{\infty }((\mathbb R^n)^m)$
satisfy
for all
![]() $|\beta |\le \big [ \frac {(m-1)n}{2} \big ]+1$
, where
$|\beta |\le \big [ \frac {(m-1)n}{2} \big ]+1$
, where
![]() $ \left [ r\right ]$
denotes the integer part of r. Then, for
$ \left [ r\right ]$
denotes the integer part of r. Then, for
![]() $f_j$
in
$f_j$
in
![]() $L^2(\mathbb {R}^n)$
,
$L^2(\mathbb {R}^n)$
,
![]() $j=1,\dots , m$
, the functions
$j=1,\dots , m$
, the functions
![]() $S_{\sigma }^{\nu }(f_1,\dots , f_m) $
converge to
$S_{\sigma }^{\nu }(f_1,\dots , f_m) $
converge to
![]() $\sigma (0) f_1 \cdots f_m$
pointwise a.e. as
$\sigma (0) f_1 \cdots f_m$
pointwise a.e. as
![]() ${\nu \to -\infty }$
and to zero pointwise a.e. as
${\nu \to -\infty }$
and to zero pointwise a.e. as
![]() $\nu \to \infty $
.
$\nu \to \infty $
.
The precise definition of the action of the multilinear operator
![]() $S_{\sigma }^{\nu }$
on
$S_{\sigma }^{\nu }$
on
![]() $L^2$
functions will be discussed after Theorem 1.4.
$L^2$
functions will be discussed after Theorem 1.4.
The a.e. convergence claimed in Theorem 1.3 is related to the boundedness of the associated m-(sub)linear lacunary maximal multiplier operator defined by
![]() $\mathscr {M}_{\sigma }$
is the so-called multilinear spherical maximal function when
$\mathscr {M}_{\sigma }$
is the so-called multilinear spherical maximal function when
![]() $\sigma =\widehat \mu $
, which was studied extensively recently by [Reference Anderson and Palsson1, Reference Barrionuevo, Grafakos, He, Honzík and Oliveira2, Reference Dosidis10, Reference Heo, Hong and Yang22, Reference Jeong and Lee23]. In particular, a bilinear version of the following theorem was previously obtained in [Reference Grafakos, He and Honzík17].
$\sigma =\widehat \mu $
, which was studied extensively recently by [Reference Anderson and Palsson1, Reference Barrionuevo, Grafakos, He, Honzík and Oliveira2, Reference Dosidis10, Reference Heo, Hong and Yang22, Reference Jeong and Lee23]. In particular, a bilinear version of the following theorem was previously obtained in [Reference Grafakos, He and Honzík17].
Theorem 1.4 Let
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $a>\frac {(m-1)n}{2}$
. Let
$a>\frac {(m-1)n}{2}$
. Let
![]() $\sigma \in \mathscr {C}^{\infty }((\mathbb R^n)^m)$
be as in Theorem 1.3. Then there exists a constant
$\sigma \in \mathscr {C}^{\infty }((\mathbb R^n)^m)$
be as in Theorem 1.3. Then there exists a constant
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} \big\Vert \mathscr{M}_{\sigma}(f_1,\dots,f_m)\big\Vert_{L^{2/m}(\mathbb R^n)}\le C \prod_{j=1}^{m}\Vert f_j\Vert_{L^2(\mathbb R^n)} \end{align*} $$
$$ \begin{align*} \big\Vert \mathscr{M}_{\sigma}(f_1,\dots,f_m)\big\Vert_{L^{2/m}(\mathbb R^n)}\le C \prod_{j=1}^{m}\Vert f_j\Vert_{L^2(\mathbb R^n)} \end{align*} $$
for Schwartz functions
![]() $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
One of the main difficulties in dealing with general m-linear cases for
![]() $m\ge 3$
is that the target space
$m\ge 3$
is that the target space
![]() $L^{2/m}$
is not a Banach space if
$L^{2/m}$
is not a Banach space if
![]() $2/m<1$
. As a result, the condition
$2/m<1$
. As a result, the condition
![]() $a>\frac {(m-1)n}{2}$
cannot be exploited by a simple adaptation of the bilinear argument in [Reference Grafakos, He and Honzík17]. Additional combinatorial complexity arises from the multilinear extension, and in order to address these issues, we apply a more refined decomposition, recently introduced in [Reference Grafakos, He, Honzík and Park18], so that l-linear Plancherel-type estimates (
$a>\frac {(m-1)n}{2}$
cannot be exploited by a simple adaptation of the bilinear argument in [Reference Grafakos, He and Honzík17]. Additional combinatorial complexity arises from the multilinear extension, and in order to address these issues, we apply a more refined decomposition, recently introduced in [Reference Grafakos, He, Honzík and Park18], so that l-linear Plancherel-type estimates (
![]() $1\le l\le m$
) can be applied. These key estimates are stated in Proposition 2.1.
$1\le l\le m$
) can be applied. These key estimates are stated in Proposition 2.1.
With the help of Theorem 1.4, we notice that the multilinear operator
![]() $S_{\sigma }^{\nu }$
is also well defined for
$S_{\sigma }^{\nu }$
is also well defined for
![]() $f_j\in L^2(\mathbb {R}^n)$
. Indeed, given
$f_j\in L^2(\mathbb {R}^n)$
. Indeed, given
![]() $f_j$
in
$f_j$
in
![]() $L^2(\mathbb {R}^n)$
, we find a sequence of Schwartz functions
$L^2(\mathbb {R}^n)$
, we find a sequence of Schwartz functions
![]() $f_j^k$
that converge to
$f_j^k$
that converge to
![]() $f_j$
in
$f_j$
in
![]() $L^2(\mathbb {R}^n)$
as
$L^2(\mathbb {R}^n)$
as
![]() $k\to \infty $
. Then Theorem 1.4 implies that the sequence
$k\to \infty $
. Then Theorem 1.4 implies that the sequence
is a Cauchy sequence in
![]() $L^{2/m}$
and, thus, it has a unique limit in
$L^{2/m}$
and, thus, it has a unique limit in
![]() $L^{2/m}$
which we call
$L^{2/m}$
which we call
![]() $S_{\sigma }^{\nu }(f_1 ,\dots , f_m )$
. It is easy to verify that this limit does not depend on the choice of
$S_{\sigma }^{\nu }(f_1 ,\dots , f_m )$
. It is easy to verify that this limit does not depend on the choice of
![]() $f_j^k$
.
$f_j^k$
.
The paper is organized as follows. Section 2 is dedicated to preliminaries, introducing a wavelet decomposition that is one of the main ingredients to establish maximal inequalities in Theorems 1.2 and 1.4, and studying general properties of the decomposition. Another maximal inequality for rough singular integrals will be given in Section 3. We prove first Theorem 1.2 in Section 4 as it is necessary for the proof of Theorem 1.1 in Section 5. The proof of Theorems 1.4 and 1.3 will be given in turn in the last two sections.
2 Preliminary material
We adapt some notations and key estimates from [Reference Grafakos, He, Honzík and Park18]. For the sake of independent reading, we review the main tools and notation. We begin with certain orthonormal bases of
![]() $L^2$
due to Triebel [Reference Triebel30], that will be of great use in our work. The idea is as follows. For any fixed
$L^2$
due to Triebel [Reference Triebel30], that will be of great use in our work. The idea is as follows. For any fixed
![]() $L\in \mathbb {N}$
, one can construct real-valued compactly supported functions
$L\in \mathbb {N}$
, one can construct real-valued compactly supported functions
![]() $\psi _F, \psi _M$
in
$\psi _F, \psi _M$
in
![]() $\mathscr {C}^L(\mathbb {R})$
satisfying the following properties:
$\mathscr {C}^L(\mathbb {R})$
satisfying the following properties:
![]() ${\Vert \psi _F\Vert _{L^2(\mathbb {R})}=\Vert \psi _M\Vert _{L^2(\mathbb {R})}=1}$
,
${\Vert \psi _F\Vert _{L^2(\mathbb {R})}=\Vert \psi _M\Vert _{L^2(\mathbb {R})}=1}$
,
![]() $\int _{\mathbb {R}}{x^{\alpha }\psi _M(x)}dx=0$
for all
$\int _{\mathbb {R}}{x^{\alpha }\psi _M(x)}dx=0$
for all
![]() $0\le \alpha \le L$
, and moreover, if
$0\le \alpha \le L$
, and moreover, if
![]() $\Psi _{\vec {{G}}}$
is a function on
$\Psi _{\vec {{G}}}$
is a function on
![]() $\mathbb {R}^{mn}$
, defined by
$\mathbb {R}^{mn}$
, defined by
for
![]() $\vec {{x}}\,:=(x_1,\dots ,x_{mn})\in \mathbb {R}^{mn}$
and
$\vec {{x}}\,:=(x_1,\dots ,x_{mn})\in \mathbb {R}^{mn}$
and
![]() $\vec {{G}}:=(g_1,\dots ,g_{mn})$
in the set
$\vec {{G}}:=(g_1,\dots ,g_{mn})$
in the set
then the family of functions
forms an orthonormal basis of
![]() $L^2(\mathbb {R}^{mn})$
, where
$L^2(\mathbb {R}^{mn})$
, where
![]() $\mathcal {I}^0:=\mathcal {I}$
and for
$\mathcal {I}^0:=\mathcal {I}$
and for
![]() $\lambda \ge 1$
, we set
$\lambda \ge 1$
, we set
![]() ${\mathcal {I}^{\lambda }:=\mathcal {I}\setminus \{(F,\dots ,F)\}}$
.
${\mathcal {I}^{\lambda }:=\mathcal {I}\setminus \{(F,\dots ,F)\}}$
.
We consistently use the notation
![]() $\vec {{\xi }}\,:=(\xi _1,\dots ,\xi _m) $
for elements of
$\vec {{\xi }}\,:=(\xi _1,\dots ,\xi _m) $
for elements of
![]() $ (\mathbb R^n)^m$
,
$ (\mathbb R^n)^m$
,
![]() $\vec {{G}}:=(G_1,\dots ,G_m)\in (\{F,M\}^n)^m$
, and
$\vec {{G}}:=(G_1,\dots ,G_m)\in (\{F,M\}^n)^m$
, and
![]() $ \Psi _{\vec {{G}}}(\vec {{\xi }}\,)=\Psi _{G_1}(\xi _1)\cdots \Psi _{G_m}(\xi _m). $
For each
$ \Psi _{\vec {{G}}}(\vec {{\xi }}\,)=\Psi _{G_1}(\xi _1)\cdots \Psi _{G_m}(\xi _m). $
For each
![]() ${\vec {{k}}:=(k_1,\dots ,k_m)\in (\mathbb Z^n)^m}$
and
${\vec {{k}}:=(k_1,\dots ,k_m)\in (\mathbb Z^n)^m}$
and
![]() $\lambda \in \mathbb {N}_0$
, let
$\lambda \in \mathbb {N}_0$
, let
and
We also assume that the support of
![]() $\psi _{g_i}$
is contained in
$\psi _{g_i}$
is contained in
![]() $\{\xi \in \mathbb {R}: |\xi |\le C_0 \}$
for some
$\{\xi \in \mathbb {R}: |\xi |\le C_0 \}$
for some
![]() $C_0>1$
, which implies that
$C_0>1$
, which implies that
In other words, the support of
![]() $\Psi _{G_i,k_i}^{\lambda }$
is contained in the ball centered at
$\Psi _{G_i,k_i}^{\lambda }$
is contained in the ball centered at
![]() $2^{-\lambda }k_i$
and radius
$2^{-\lambda }k_i$
and radius
![]() $C_0\sqrt {n}2^{-\lambda }$
. Then we note that for a fixed
$C_0\sqrt {n}2^{-\lambda }$
. Then we note that for a fixed
![]() $\lambda \in \mathbb {N}_0$
, elements of
$\lambda \in \mathbb {N}_0$
, elements of
![]() $\big \{\Psi _{\vec {{G}},\vec {{k}}\,}^{\lambda }\big \}_{\vec {{k}}\,}$
have (almost) disjoint compact supports.
$\big \{\Psi _{\vec {{G}},\vec {{k}}\,}^{\lambda }\big \}_{\vec {{k}}\,}$
have (almost) disjoint compact supports.
It is also known in [Reference Triebel29] that if L is sufficiently large, then every tempered distribution H on
![]() $\mathbb {R}^{mn}$
can be represented as
$\mathbb {R}^{mn}$
can be represented as
and for
![]() $1<q<\infty $
and
$1<q<\infty $
and
![]() $s\ge 0$
,
$s\ge 0$
,
 $$ \begin{align*}\Big\Vert \Big(\sum_{\vec G,\ \vec k} \big|b_{\vec G,\vec k}^{\lambda} \Psi^{\lambda}_{\vec G,\vec k}\big|^2\Big)^{1/2} \Big\Vert_{L^q(\mathbb{R}^{mn})} \le C2^{-s\lambda}\|H\|_{L^q_s(\mathbb{R}^{mn})}, \end{align*} $$
$$ \begin{align*}\Big\Vert \Big(\sum_{\vec G,\ \vec k} \big|b_{\vec G,\vec k}^{\lambda} \Psi^{\lambda}_{\vec G,\vec k}\big|^2\Big)^{1/2} \Big\Vert_{L^q(\mathbb{R}^{mn})} \le C2^{-s\lambda}\|H\|_{L^q_s(\mathbb{R}^{mn})}, \end{align*} $$
where
and
![]() $L^q_s$
is the Sobolev space of functions H such that
$L^q_s$
is the Sobolev space of functions H such that
![]() $(I-\Delta )^{s/2} H \in L^q(\mathbb R^{mn})$
. Moreover, it follows from the last estimate and from the (almost) disjoint support property of the
$(I-\Delta )^{s/2} H \in L^q(\mathbb R^{mn})$
. Moreover, it follows from the last estimate and from the (almost) disjoint support property of the
![]() $\Psi ^{\lambda }_{\vec G,\vec k}$
’s that
$\Psi ^{\lambda }_{\vec G,\vec k}$
’s that
 $$ \begin{align} \big\Vert \big\{b_{\vec{{G}},\vec{{k}}\,}^{\lambda}\big\}_{\vec{{k}}\,\in \mathbb{Z}^{mn}}\big\Vert_{\ell^{q}} \approx&\Big(2^{\lambda mn(1-q/2)}\int_{\mathbb{R}^{mn}}\Big( \sum_{\vec{{k}}\,} \big|b^{\lambda}_{\vec G,\vec k}\Psi^{\lambda}_{\vec G,\vec k}(\vec x)\big|^2\Big)^{q/2}~ d\vec{{x}}\,\Big)^{1/q}\notag \\ \lesssim& \; 2^{-\lambda (s-mn/q+mn/2)}\Vert H\Vert_{L^q_s(\mathbb{R}^{mn})}. \end{align} $$
$$ \begin{align} \big\Vert \big\{b_{\vec{{G}},\vec{{k}}\,}^{\lambda}\big\}_{\vec{{k}}\,\in \mathbb{Z}^{mn}}\big\Vert_{\ell^{q}} \approx&\Big(2^{\lambda mn(1-q/2)}\int_{\mathbb{R}^{mn}}\Big( \sum_{\vec{{k}}\,} \big|b^{\lambda}_{\vec G,\vec k}\Psi^{\lambda}_{\vec G,\vec k}(\vec x)\big|^2\Big)^{q/2}~ d\vec{{x}}\,\Big)^{1/q}\notag \\ \lesssim& \; 2^{-\lambda (s-mn/q+mn/2)}\Vert H\Vert_{L^q_s(\mathbb{R}^{mn})}. \end{align} $$
Now we study an essential estimate in [Reference Grafakos, He, Honzík and Park18] which will play a significant role in the proof of both Theorems 1.2 and 1.4. We define the operator
![]() $L_{G_i,k_i}^{\lambda ,\gamma }$
by
$L_{G_i,k_i}^{\lambda ,\gamma }$
by
For
![]() $\mu \in \mathbb {Z}$
, let
$\mu \in \mathbb {Z}$
, let
and split the set into m disjoint subsets
![]() $\mathcal {U}_l^{\mu }$
as below:
$\mathcal {U}_l^{\mu }$
as below:
 $$ \begin{align*} \mathcal{U}_1^{{\mu}}&:=\big\{\vec{{k}}\,\in \mathcal{U}^{{\mu}}:|k_1|\ge 2C_0\sqrt{n}>|k_2|\ge\cdots \ge |k_m| \big\}\\ \mathcal{U}_2^{{\mu}}&:=\big\{\vec{{k}}\,\in \mathcal{U}^{{\mu}}:|k_1|\ge |k_2|\ge 2C_0\sqrt{n}>|k_3|\ge\cdots \ge |k_m| \big\}\\ &\vdots\\ \mathcal{U}_m^{{\mu}}&:=\big\{\vec{{k}}\,\in \mathcal{U}^{{\mu}}:|k_1|\ge \cdots\ge |k_m|\ge 2C_0\sqrt{n} \big\}. \end{align*} $$
$$ \begin{align*} \mathcal{U}_1^{{\mu}}&:=\big\{\vec{{k}}\,\in \mathcal{U}^{{\mu}}:|k_1|\ge 2C_0\sqrt{n}>|k_2|\ge\cdots \ge |k_m| \big\}\\ \mathcal{U}_2^{{\mu}}&:=\big\{\vec{{k}}\,\in \mathcal{U}^{{\mu}}:|k_1|\ge |k_2|\ge 2C_0\sqrt{n}>|k_3|\ge\cdots \ge |k_m| \big\}\\ &\vdots\\ \mathcal{U}_m^{{\mu}}&:=\big\{\vec{{k}}\,\in \mathcal{U}^{{\mu}}:|k_1|\ge \cdots\ge |k_m|\ge 2C_0\sqrt{n} \big\}. \end{align*} $$
Then we have the following two observations that appear in [Reference Grafakos, He, Honzík and Park18].
-
• For
 $\vec {{k}}\,\in \mathcal {U}_l^{\lambda +\mu }$
, (2.5)due to the support of
$\vec {{k}}\,\in \mathcal {U}_l^{\lambda +\mu }$
, (2.5)due to the support of $$ \begin{align} L_{G_j,k_j}^{\lambda,\gamma}f=L_{G_j,k_j}^{\lambda,\gamma}f^{\lambda,\gamma,{\mu}} \quad \text{ for }~ 1\le j\le l \end{align} $$
$$ \begin{align} L_{G_j,k_j}^{\lambda,\gamma}f=L_{G_j,k_j}^{\lambda,\gamma}f^{\lambda,\gamma,{\mu}} \quad \text{ for }~ 1\le j\le l \end{align} $$
 $\Psi _{G_j,k_j}^{\lambda }$
, where
$\Psi _{G_j,k_j}^{\lambda }$
, where
 $\widehat {f^{\lambda ,\gamma ,\mu }}(\xi ):=\widehat {f}(\xi )\chi _{C_0\sqrt {n}2^{\gamma -\lambda }\le |\xi |\le 2^{\gamma +\mu +3}}$
.
$\widehat {f^{\lambda ,\gamma ,\mu }}(\xi ):=\widehat {f}(\xi )\chi _{C_0\sqrt {n}2^{\gamma -\lambda }\le |\xi |\le 2^{\gamma +\mu +3}}$
.
-
• For
 $\mu \ge 1$
and
$\mu \ge 1$
and
 $\lambda \in \mathbb {N}_0$
, (2.6)where Plancherel’s identity is applied in the first inequality.
$\lambda \in \mathbb {N}_0$
, (2.6)where Plancherel’s identity is applied in the first inequality. $$ \begin{align} \Big( \sum_{\gamma\in\mathbb{Z}}{\big\Vert f^{\lambda,\gamma,{\mu}}\big\Vert_{L^2}^2}\Big)^{1/2}\lesssim ({\mu}+\lambda)^{1/2}\Vert f\Vert_{L^2} \lesssim \mu^{1/2}(\lambda+1)^{1/2}\Vert f\Vert_{L^2} \end{align} $$
$$ \begin{align} \Big( \sum_{\gamma\in\mathbb{Z}}{\big\Vert f^{\lambda,\gamma,{\mu}}\big\Vert_{L^2}^2}\Big)^{1/2}\lesssim ({\mu}+\lambda)^{1/2}\Vert f\Vert_{L^2} \lesssim \mu^{1/2}(\lambda+1)^{1/2}\Vert f\Vert_{L^2} \end{align} $$
Proposition 2.1 [Reference Grafakos, He, Honzík and Park18, Proposition 2.4]
Let m be a positive integer with
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $0<q<\frac {2m}{m-1}$
. Fix
$0<q<\frac {2m}{m-1}$
. Fix
![]() $\lambda \in \mathbb {N}_0$
and
$\lambda \in \mathbb {N}_0$
and
![]() $\vec {{G}}\in \mathcal {I}^{\lambda }$
. Suppose that
$\vec {{G}}\in \mathcal {I}^{\lambda }$
. Suppose that
![]() $\{b_{\vec {{G}},\vec {{k}}\,}^{\lambda ,\gamma ,\mu }\}_{\vec {{G}}\in \mathcal {I}^{\lambda }, \gamma ,\mu \in \mathbb {Z}, \vec {{k}}\,\in (\mathbb Z^n)^m}$
is a sequence of complex numbers satisfying
$\{b_{\vec {{G}},\vec {{k}}\,}^{\lambda ,\gamma ,\mu }\}_{\vec {{G}}\in \mathcal {I}^{\lambda }, \gamma ,\mu \in \mathbb {Z}, \vec {{k}}\,\in (\mathbb Z^n)^m}$
is a sequence of complex numbers satisfying
and
Then the following statements hold:
-
(1) For
 $1\le r\le 2$
, there exists a constant
$1\le r\le 2$
, there exists a constant
 $C>0$
, independent of
$C>0$
, independent of
 $,\vec {{G}}, \lambda , \mu $
, such that
$,\vec {{G}}, \lambda , \mu $
, such that  $$ \begin{align*} &\Big\Vert \bigg(\sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in \mathcal{U}_1^{\lambda+\mu}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu}L_{G_1,k_1}^{\lambda,\gamma}f_1^{\lambda,\gamma,\mu}\prod _{j=2}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j\Big|^r\bigg)^{1/r}\Big\Vert_{L^{2/m}}\\ &\le C A_{\vec{{G}},\lambda,\mu} 2^{\lambda mn/2}\Big(\sum_{\gamma\in\mathbb{Z}}{\Vert f_1^{\lambda,\gamma,\mu}\Vert_{L^2}^r} \Big)^{1/r} \prod_{j=2}^{m}\Vert f_{j}\Vert_{L^2} \end{align*} $$
$$ \begin{align*} &\Big\Vert \bigg(\sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in \mathcal{U}_1^{\lambda+\mu}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu}L_{G_1,k_1}^{\lambda,\gamma}f_1^{\lambda,\gamma,\mu}\prod _{j=2}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j\Big|^r\bigg)^{1/r}\Big\Vert_{L^{2/m}}\\ &\le C A_{\vec{{G}},\lambda,\mu} 2^{\lambda mn/2}\Big(\sum_{\gamma\in\mathbb{Z}}{\Vert f_1^{\lambda,\gamma,\mu}\Vert_{L^2}^r} \Big)^{1/r} \prod_{j=2}^{m}\Vert f_{j}\Vert_{L^2} \end{align*} $$
for Schwartz functions
 $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
 $\mathbb R^n$
.
$\mathbb R^n$
. -
(2) For
 $2\le l\le m$
, there exists a constant
$2\le l\le m$
, there exists a constant
 $C>0$
, independent of
$C>0$
, independent of
 $\vec {{G}}, \lambda , \mu $
, such that
$\vec {{G}}, \lambda , \mu $
, such that  $$ \begin{align*} &\Big\Vert \sum_{\gamma\in\mathbb{Z}} \Big| \sum_{\vec{{k}}\,\in \mathcal{U}_l^{\lambda+\mu}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu}\bigg( \prod_{j=1}^{l}L_{G_j,k_j}^{\lambda,\gamma}f_j^{\lambda,\gamma,\mu}\bigg)\bigg( \prod_{j=l+1}^{m}L_{G_j,k_{j}}^{\lambda,\gamma}f_{j}\bigg) \Big| \Big\Vert_{L^{2/m}}\\ &\le C A_{\vec{{G}},\lambda,\mu}^{1-\frac{(l-1)q}{2l}}B_{\vec{{G}},\lambda,\mu,q}^{\frac{(l-1)q}{2l}} 2^{\lambda mn/2}\bigg[ \prod_{j=1}^{l}\Big(\sum_{\gamma\in\mathbb{Z}}{\Vert f_j^{\lambda,\gamma,\mu}\Vert_{L^2}^2} \Big)^{1/2}\bigg] \bigg[\prod_{j=l+1}^{m}\Vert f_{j}\Vert_{L^2}\bigg] \end{align*} $$
$$ \begin{align*} &\Big\Vert \sum_{\gamma\in\mathbb{Z}} \Big| \sum_{\vec{{k}}\,\in \mathcal{U}_l^{\lambda+\mu}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu}\bigg( \prod_{j=1}^{l}L_{G_j,k_j}^{\lambda,\gamma}f_j^{\lambda,\gamma,\mu}\bigg)\bigg( \prod_{j=l+1}^{m}L_{G_j,k_{j}}^{\lambda,\gamma}f_{j}\bigg) \Big| \Big\Vert_{L^{2/m}}\\ &\le C A_{\vec{{G}},\lambda,\mu}^{1-\frac{(l-1)q}{2l}}B_{\vec{{G}},\lambda,\mu,q}^{\frac{(l-1)q}{2l}} 2^{\lambda mn/2}\bigg[ \prod_{j=1}^{l}\Big(\sum_{\gamma\in\mathbb{Z}}{\Vert f_j^{\lambda,\gamma,\mu}\Vert_{L^2}^2} \Big)^{1/2}\bigg] \bigg[\prod_{j=l+1}^{m}\Vert f_{j}\Vert_{L^2}\bigg] \end{align*} $$
for Schwartz functions
 $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
 $\mathbb R^n$
, where
$\mathbb R^n$
, where
 $\prod _{m+1}^m$
is understood as the function 1.
$\prod _{m+1}^m$
is understood as the function 1.
In view of (2.5), (2.6), and Proposition 2.1, we actually obtain
 $$ \begin{align} &\Big\Vert \bigg( \sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{1}^{\lambda+\mu}}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu} \prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j\Big|^2\bigg)^{1/2}\Big\Vert_{L^{2/m}}\nonumber \\ &\lesssim A_{\vec{{G}},\lambda,\mu}\mu^{1/2}2^{\lambda mn/2}(\lambda+1)^{1/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align} $$
$$ \begin{align} &\Big\Vert \bigg( \sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{1}^{\lambda+\mu}}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu} \prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j\Big|^2\bigg)^{1/2}\Big\Vert_{L^{2/m}}\nonumber \\ &\lesssim A_{\vec{{G}},\lambda,\mu}\mu^{1/2}2^{\lambda mn/2}(\lambda+1)^{1/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align} $$
and for
![]() $2\le l\le m$
,
$2\le l\le m$
,
 $$ \begin{align} &\Big\Vert \sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{l}^{\lambda+\mu}}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu}\prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j\Big| \Big\Vert_{L^{2/m}}\nonumber\\ &\lesssim A_{\vec{{G}},\lambda,\mu}^{1-\frac{(l-1)q}{2l}}B_{\vec{{G}},\lambda,\mu,q}^{\frac{(l-1)q}{2l}} \mu^{l/2}2^{\lambda mn/2}(\lambda+1)^{l/2} \prod_{j=1}^{m}\Vert f_{j}\Vert_{L^2}. \end{align} $$
$$ \begin{align} &\Big\Vert \sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{l}^{\lambda+\mu}}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\gamma,\mu}\prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j\Big| \Big\Vert_{L^{2/m}}\nonumber\\ &\lesssim A_{\vec{{G}},\lambda,\mu}^{1-\frac{(l-1)q}{2l}}B_{\vec{{G}},\lambda,\mu,q}^{\frac{(l-1)q}{2l}} \mu^{l/2}2^{\lambda mn/2}(\lambda+1)^{l/2} \prod_{j=1}^{m}\Vert f_{j}\Vert_{L^2}. \end{align} $$
3 An auxiliary lemma
We have the following extension of Lemma 5 in [Reference Buriánková and Honzík3].
Lemma 3.1 Let
![]() $1<q\le \infty $
and
$1<q\le \infty $
and
![]() $\Omega \in L^q(\mathbb S^{mn-1})$
. Suppose
$\Omega \in L^q(\mathbb S^{mn-1})$
. Suppose
![]() $1<p_1,\dots , p_m<\infty $
and
$1<p_1,\dots , p_m<\infty $
and
![]() $1/m<p<\infty $
satisfies
$1/m<p<\infty $
satisfies
![]() $1/p=1/p_1+\cdots +1/p_m$
and
$1/p=1/p_1+\cdots +1/p_m$
and
Given
![]() $f_j\in L^{p_j}(\mathbb {R}^n)$
, there is a set of measure zero E such that for
$f_j\in L^{p_j}(\mathbb {R}^n)$
, there is a set of measure zero E such that for
![]() $x\in \mathbb R^n\setminus E$
,
$x\in \mathbb R^n\setminus E$
,
 $$ \begin{align} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\, <\infty, \end{align} $$
$$ \begin{align} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\, <\infty, \end{align} $$
for all
![]() $R>0$
. Then, for
$R>0$
. Then, for
![]() $x\in \mathbb R^n\setminus E$
, the maximal operator
$x\in \mathbb R^n\setminus E$
, the maximal operator
 $$ \begin{align} \mathcal M_{\Omega}(f_1,\dots, f_m)(x)= \sup_{R>0} \frac{1}{R^{mn} } \idotsint\limits_{|\vec y|\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\, \end{align} $$
$$ \begin{align} \mathcal M_{\Omega}(f_1,\dots, f_m)(x)= \sup_{R>0} \frac{1}{R^{mn} } \idotsint\limits_{|\vec y|\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\, \end{align} $$
is well defined and maps
![]() $L^{p_1}(\mathbb R^n) \times \cdots \times L^{p_m}(\mathbb R^n) $
to
$L^{p_1}(\mathbb R^n) \times \cdots \times L^{p_m}(\mathbb R^n) $
to
![]() $L^{p }(\mathbb R^n) $
with norm bounded by a constant multiple of
$L^{p }(\mathbb R^n) $
with norm bounded by a constant multiple of
![]() $\|\Omega \|_{L^q(\mathbb {S}^{mn-1})}$
. Precisely, there is a constant
$\|\Omega \|_{L^q(\mathbb {S}^{mn-1})}$
. Precisely, there is a constant
![]() $C>0$
such that
$C>0$
such that
for functions
![]() $f_j\in L^{p_j}(\mathbb {R}^n)$
,
$f_j\in L^{p_j}(\mathbb {R}^n)$
,
![]() $1\le j\le m$
.
$1\le j\le m$
.
Proof Since
![]() $\Vert \Omega \Vert _{L^r(\mathbb {S}^{mn-1})}\lesssim \Vert \Omega \Vert _{L^{\infty }(\mathbb {S}^{mn-1})}$
for all
$\Vert \Omega \Vert _{L^r(\mathbb {S}^{mn-1})}\lesssim \Vert \Omega \Vert _{L^{\infty }(\mathbb {S}^{mn-1})}$
for all
![]() $1<r<\infty $
and there exists
$1<r<\infty $
and there exists
![]() $1<q<\infty $
such that
$1<q<\infty $
such that
![]() $1/p<1/q+m/q'<m~ (=1/\infty +m/1)$
, we may assume that
$1/p<1/q+m/q'<m~ (=1/\infty +m/1)$
, we may assume that
![]() $1<q<\infty $
. Without loss of generality, we may also assume that
$1<q<\infty $
. Without loss of generality, we may also assume that
![]() $\|\Omega \|_{L^q(\mathbb {S}^{mn-1})}=1$
.
$\|\Omega \|_{L^q(\mathbb {S}^{mn-1})}=1$
.
We split
 $$\begin{align*}\Omega= \Omega_0+\sum_{l=1}^{\infty} \Omega_l , \end{align*}$$
$$\begin{align*}\Omega= \Omega_0+\sum_{l=1}^{\infty} \Omega_l , \end{align*}$$
where
![]() $\Omega _0=\Omega \chi _{|\Omega |\le 2}$
and
$\Omega _0=\Omega \chi _{|\Omega |\le 2}$
and
![]() $\Omega _l=\Omega \chi _{2^l<|\Omega |\le 2^{l+1} }$
for
$\Omega _l=\Omega \chi _{2^l<|\Omega |\le 2^{l+1} }$
for
![]() $l\ge 1$
. Then Hölder’s inequality and Chebyshev’s inequality give
$l\ge 1$
. Then Hölder’s inequality and Chebyshev’s inequality give
and obviously,
We first claim that for
![]() $1<r,r_1,\dots ,r_m<\infty $
with
$1<r,r_1,\dots ,r_m<\infty $
with
![]() $1/r=1/r_1+\cdots +1/r_m$
, we have
$1/r=1/r_1+\cdots +1/r_m$
, we have
 $$ \begin{align} \big\|\mathcal M_{\Omega_l} (S_1,\dots, S_m) \big\|_{L^{r_1}\times \cdots \times L^{r_m}\to L^{r}} \lesssim 2^{-l \frac{q}{q'}} \prod_{j=1}^m\|S_j\|_{L^{r_j}(\mathbb{R}^n)} \end{align} $$
$$ \begin{align} \big\|\mathcal M_{\Omega_l} (S_1,\dots, S_m) \big\|_{L^{r_1}\times \cdots \times L^{r_m}\to L^{r}} \lesssim 2^{-l \frac{q}{q'}} \prod_{j=1}^m\|S_j\|_{L^{r_j}(\mathbb{R}^n)} \end{align} $$
for simple functions
![]() $S_j$
. To verify this estimate, we choose indices
$S_j$
. To verify this estimate, we choose indices
![]() $\mu _1,\dots ,\mu _m$
satisfying
$\mu _1,\dots ,\mu _m$
satisfying
and
Then a direct computation using Hölder’s inequality yields
 $$\begin{align*}\mathcal M_{\Omega_l}\big(S_1,\dots, S_m\big)(x) \le \int_{\mathbb S^{mn-1}} \big|\Omega_l (\vec \theta\, )\big| \prod_{j=1}^{m}\mathcal{M}_{\mu_j}^{\theta_j}S_j(x) ~ d\vec \theta\, , \end{align*}$$
$$\begin{align*}\mathcal M_{\Omega_l}\big(S_1,\dots, S_m\big)(x) \le \int_{\mathbb S^{mn-1}} \big|\Omega_l (\vec \theta\, )\big| \prod_{j=1}^{m}\mathcal{M}_{\mu_j}^{\theta_j}S_j(x) ~ d\vec \theta\, , \end{align*}$$
where the directional maximal operator
![]() $\mathcal {M}_{\mu _j}^{\theta _j}$
is defined by
$\mathcal {M}_{\mu _j}^{\theta _j}$
is defined by
 $$\begin{align*}\mathcal M_{\mu_j}^{\theta_j} g(x) := \sup_{R>0}\Big( \frac{1}{R }\int_0^R \big| g (x-t\theta_j) \big|^{\mu_j} ~dt\Big)^{1/\mu_j}. \end{align*}$$
$$\begin{align*}\mathcal M_{\mu_j}^{\theta_j} g(x) := \sup_{R>0}\Big( \frac{1}{R }\int_0^R \big| g (x-t\theta_j) \big|^{\mu_j} ~dt\Big)^{1/\mu_j}. \end{align*}$$
It follows from this that
 $$\begin{align*}\big\| \mathcal M_{\Omega_l}(S_1,\dots, S_m)\big\|_{L^{r}} \le \int_{\mathbb S^{mn-1}} |\Omega_l (\vec \theta\, ) | \prod_{j=1}^m \big\| \mathcal M_{\mu_j}^{\theta_j}S_j \big\|_{L^{r_j}} ~ d\vec \theta, \end{align*}$$
$$\begin{align*}\big\| \mathcal M_{\Omega_l}(S_1,\dots, S_m)\big\|_{L^{r}} \le \int_{\mathbb S^{mn-1}} |\Omega_l (\vec \theta\, ) | \prod_{j=1}^m \big\| \mathcal M_{\mu_j}^{\theta_j}S_j \big\|_{L^{r_j}} ~ d\vec \theta, \end{align*}$$
where Minkowski’s inequality and Hölder’s inequality are applied. Using the
![]() $L^{r_j}$
boundedness of
$L^{r_j}$
boundedness of
![]() $\mathcal M_{\mu _j}^{\theta _j} $
for
$\mathcal M_{\mu _j}^{\theta _j} $
for
![]() $0<\mu _j<r_j$
with constants independent of
$0<\mu _j<r_j$
with constants independent of
![]() $\theta _j$
(by the method of rotations), we obtain (3.6).
$\theta _j$
(by the method of rotations), we obtain (3.6).
Then the case
![]() $p>1$
(for which
$p>1$
(for which
![]() $q>1$
implies the assumption (3.1)) in the assertion follows from summing the estimates (3.6) over
$q>1$
implies the assumption (3.1)) in the assertion follows from summing the estimates (3.6) over
![]() $l\ge 0$
.
$l\ge 0$
.
The other case
![]() $1/m<p\le 1$
can be proved by interpolation with the
$1/m<p\le 1$
can be proved by interpolation with the
![]() $L^1\times \cdots \times L^1\to L^{1/m,\infty }$
estimate. Let
$L^1\times \cdots \times L^1\to L^{1/m,\infty }$
estimate. Let
![]() $\mathcal {M}$
be the Hardy–Littlewood maximal operator. Then, using (3.5), it is easy to verify the pointwise estimate
$\mathcal {M}$
be the Hardy–Littlewood maximal operator. Then, using (3.5), it is easy to verify the pointwise estimate
 $$\begin{align*}\mathcal M_{\Omega_l}\big(f_1,\dots , f_m\big)(x) \le 2^{l+1} \prod_{j=1}^m \mathcal M f_j(x), \end{align*}$$
$$\begin{align*}\mathcal M_{\Omega_l}\big(f_1,\dots , f_m\big)(x) \le 2^{l+1} \prod_{j=1}^m \mathcal M f_j(x), \end{align*}$$
for
![]() $f_1,\dots , f_m$
in
$f_1,\dots , f_m$
in
![]() $L^1(\mathbb R^n)$
, and this yields that
$L^1(\mathbb R^n)$
, and this yields that
using Hölder’s inequality for weak-type spaces [Reference Grafakos14, p. 16] and the weak
![]() $(1,1)$
boundedness of
$(1,1)$
boundedness of
![]() $\mathcal {M}$
. Now we fix
$\mathcal {M}$
. Now we fix
![]() $0<p_1,\dots ,p_m<\infty $
and
$0<p_1,\dots ,p_m<\infty $
and
![]() $1/m<p\le 1$
, and choose
$1/m<p\le 1$
, and choose
![]() $r>1$
such that
$r>1$
such that
 $$ \begin{align*} \frac{1}{p}<\frac{1}{rq}+\frac{m}{q'} \,\,\,\bigg( \!\!<\frac{1}{q}+\frac{m}{q'} \bigg), \end{align*} $$
$$ \begin{align*} \frac{1}{p}<\frac{1}{rq}+\frac{m}{q'} \,\,\,\bigg( \!\!<\frac{1}{q}+\frac{m}{q'} \bigg), \end{align*} $$
or, equivalently,
 $$ \begin{align*}\frac{q(m-1/p)}{q'(m-1/r)}-\frac{1/p-1/r}{m-1/r}>0.\end{align*} $$
$$ \begin{align*}\frac{q(m-1/p)}{q'(m-1/r)}-\frac{1/p-1/r}{m-1/r}>0.\end{align*} $$
Interpolating between (3.7) and (3.6) with appropriate
![]() $(r_1,\dots , r_m)$
satisfying
$(r_1,\dots , r_m)$
satisfying
![]() $1/r=1/r_1+\dots +1/r_m$
(using [Reference Grafakos15, Theorem 7.2.2]) yields
$1/r=1/r_1+\dots +1/r_m$
(using [Reference Grafakos15, Theorem 7.2.2]) yields
for simple functions
![]() $S_j$
. The exponential decay in l obtained above together with the fact that
$S_j$
. The exponential decay in l obtained above together with the fact that
![]() $\|\cdot \|_{L^p}^p$
is a subadditive quantity for
$\|\cdot \|_{L^p}^p$
is a subadditive quantity for
![]() $0<p\le 1$
implies, for p and q satisfying (3.1),
$0<p\le 1$
implies, for p and q satisfying (3.1),
for simple functions
![]() $S_1,\dots , S_m$
.
$S_1,\dots , S_m$
.
Next, we extend
![]() $\mathcal M_{\Omega }(f_1,\dots , f_m)$
to functions
$\mathcal M_{\Omega }(f_1,\dots , f_m)$
to functions
![]() $f_j\in L^{p_j}(\mathbb {R}^n).$
To achieve this goal, we choose nonnegative simple functions
$f_j\in L^{p_j}(\mathbb {R}^n).$
To achieve this goal, we choose nonnegative simple functions
![]() $S_j^k$
that increase pointwise to
$S_j^k$
that increase pointwise to
![]() $|f_j|$
as
$|f_j|$
as
![]() $k\to \infty $
.
$k\to \infty $
.
It follows from (3.8) that for any
![]() $R>0$
,
$R>0$
,
 $$\begin{align*}\bigg\{\int_{\mathbb R^{n}} \bigg[ \frac{1}{R^{mn}} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m S_j^k(x-y_j) ~ d\vec{{y}}\, \bigg]^{p} dx \bigg\}^{\frac 1p}\le C\,\|f_1\|_{L^{p_1}}\cdots\|f_m\|_{L^{p_m}}, \end{align*}$$
$$\begin{align*}\bigg\{\int_{\mathbb R^{n}} \bigg[ \frac{1}{R^{mn}} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m S_j^k(x-y_j) ~ d\vec{{y}}\, \bigg]^{p} dx \bigg\}^{\frac 1p}\le C\,\|f_1\|_{L^{p_1}}\cdots\|f_m\|_{L^{p_m}}, \end{align*}$$
and from this, we obtain
 $$\begin{align*}\bigg\{\int_{\mathbb R^{n}} \bigg[ \frac{1}{R^{mn}} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m |f_j^k(x-y_j)| ~ d\vec{{y}}\, \bigg]^{p} dx \bigg\}^{\frac 1p}\le C\, \|f_1\|_{L^{p_1}}\cdots\|f_m\|_{L^{p_m}} \end{align*}$$
$$\begin{align*}\bigg\{\int_{\mathbb R^{n}} \bigg[ \frac{1}{R^{mn}} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m |f_j^k(x-y_j)| ~ d\vec{{y}}\, \bigg]^{p} dx \bigg\}^{\frac 1p}\le C\, \|f_1\|_{L^{p_1}}\cdots\|f_m\|_{L^{p_m}} \end{align*}$$
via Lebesgue’s monotone convergence theorem. We conclude that for any
![]() $R\in \mathbb Z^+$
, there is a set of measure zero
$R\in \mathbb Z^+$
, there is a set of measure zero
![]() $E^R$
such that
$E^R$
such that
 $$ \begin{align} \frac{1}{R^{mn}} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m |f_j^k(x-y_j)| ~ d\vec{{y}}\, <\infty \end{align} $$
$$ \begin{align} \frac{1}{R^{mn}} \idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m |f_j^k(x-y_j)| ~ d\vec{{y}}\, <\infty \end{align} $$
for all
![]() $x\in \mathbb R^n\setminus E^R$
. Setting
$x\in \mathbb R^n\setminus E^R$
. Setting
![]() $E= \cup _{R=1}^{\infty } E^R$
, we obtain (3.2) for
$E= \cup _{R=1}^{\infty } E^R$
, we obtain (3.2) for
![]() $x\in \mathbb R^n\setminus E$
.
$x\in \mathbb R^n\setminus E$
.
This allows us to define
![]() $\mathcal M_{\Omega }(f_1,\dots , f_m)(x) $
for
$\mathcal M_{\Omega }(f_1,\dots , f_m)(x) $
for
![]() $f_j\in L^{p_j}(\mathbb {R}^n)$
and
$f_j\in L^{p_j}(\mathbb {R}^n)$
and
![]() $x\in \mathbb R^n\setminus E$
as the supremum of the expressions in (3.9). Now, for
$x\in \mathbb R^n\setminus E$
as the supremum of the expressions in (3.9). Now, for
![]() $x\in \mathbb R^n\setminus E$
,
$x\in \mathbb R^n\setminus E$
,
 $$ \begin{align*} \mathcal M_{\Omega}(f_1,\dots, f_m)(x)= &\sup_{R>0}\frac1{R^{mn}}\idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\,\\ =&\sup_{R>0}\lim_{k\to\infty} \frac1{R^{mn}}\idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m S^k_j(x-y_j) ~ d\vec{{y}}\,\\ \le&\liminf_{k\to\infty} \mathcal M_{\Omega}(S^k_1,\dots, S^k_m)(x). \end{align*} $$
$$ \begin{align*} \mathcal M_{\Omega}(f_1,\dots, f_m)(x)= &\sup_{R>0}\frac1{R^{mn}}\idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\,\\ =&\sup_{R>0}\lim_{k\to\infty} \frac1{R^{mn}}\idotsint\limits_{|\vec y\, |\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m S^k_j(x-y_j) ~ d\vec{{y}}\,\\ \le&\liminf_{k\to\infty} \mathcal M_{\Omega}(S^k_1,\dots, S^k_m)(x). \end{align*} $$
As
![]() $\mathcal M_{\Omega }(S^k_1,\dots , S^k_m)(x)$
is increasing in k, we obtain from (3.8) by Fatou’s lemma that
$\mathcal M_{\Omega }(S^k_1,\dots , S^k_m)(x)$
is increasing in k, we obtain from (3.8) by Fatou’s lemma that
 $$ \begin{align*}\| \mathcal M_{\Omega}(f_1,\dots, f_m)\|_{L^p(\mathbb{R}^n)} \lesssim \liminf_{k\to\infty} \|\mathcal M_{\Omega}(S^k_1,\dots, S^k_m)\|_{L^p(\mathbb{R}^n)} \lesssim \prod_{j=1}^m\|f_j\|_{L^{p_j}(\mathbb{R}^n)}. \end{align*} $$
$$ \begin{align*}\| \mathcal M_{\Omega}(f_1,\dots, f_m)\|_{L^p(\mathbb{R}^n)} \lesssim \liminf_{k\to\infty} \|\mathcal M_{\Omega}(S^k_1,\dots, S^k_m)\|_{L^p(\mathbb{R}^n)} \lesssim \prod_{j=1}^m\|f_j\|_{L^{p_j}(\mathbb{R}^n)}. \end{align*} $$
In particular, this shows that for
![]() $f_j\in L^{p_j}(\mathbb {R}^n)$
, there is a set
$f_j\in L^{p_j}(\mathbb {R}^n)$
, there is a set
![]() $E'$
of measure zero such that
$E'$
of measure zero such that
 $$\begin{align*}\sup_{R>0} \frac{1}{R^{mn} } \idotsint\limits_{|\vec y|\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\,<\infty \end{align*}$$
$$\begin{align*}\sup_{R>0} \frac{1}{R^{mn} } \idotsint\limits_{|\vec y|\le R} |\Omega (\vec{{y}}\,' ) | \prod_{j=1}^m \big| f_j(x-y_j) \big| ~ d\vec{{y}}\,<\infty \end{align*}$$
for all.
![]() $x\in \mathbb {R}^n\setminus E'$
3.9
$x\in \mathbb {R}^n\setminus E'$
3.9
4 Proof of Theorem 1.2
Let
![]() $\frac {2m}{m+1}<q<2$
and
$\frac {2m}{m+1}<q<2$
and
![]() $\Omega $
in
$\Omega $
in
![]() $L^q(\mathbb S^{mn-1})$
. We use a dyadic decomposition introduced by Duoandikoetxea and Rubio de Francia [Reference Duoandikoetxea and Rubio de Francia13]. We choose a Schwartz function
$L^q(\mathbb S^{mn-1})$
. We use a dyadic decomposition introduced by Duoandikoetxea and Rubio de Francia [Reference Duoandikoetxea and Rubio de Francia13]. We choose a Schwartz function
![]() $\Phi ^{(m)}$
on
$\Phi ^{(m)}$
on
![]() $(\mathbb R^n)^m$
such that its Fourier transform
$(\mathbb R^n)^m$
such that its Fourier transform
![]() $\widehat {\Phi ^{(m)}}$
is supported in the annulus
$\widehat {\Phi ^{(m)}}$
is supported in the annulus
![]() $\{\vec {{\xi }}\,\in (\mathbb R^n)^m: 1/2\le |\vec {{\xi }}\,|\le 2\}$
and satisfies
$\{\vec {{\xi }}\,\in (\mathbb R^n)^m: 1/2\le |\vec {{\xi }}\,|\le 2\}$
and satisfies
![]() $\sum _{j\in \mathbb {Z}}\widehat {\Phi ^{(m)}_j}(\vec {{\xi }}\,)=1$
for
$\sum _{j\in \mathbb {Z}}\widehat {\Phi ^{(m)}_j}(\vec {{\xi }}\,)=1$
for
![]() $\vec {{\xi }}\,\not = \vec {\boldsymbol {0}}$
where
$\vec {{\xi }}\,\not = \vec {\boldsymbol {0}}$
where
![]() $\widehat {\Phi _j^{(m)}}(\vec {{\xi }}\,):=\widehat {\Phi ^{(m)}}(\vec {{\xi }}\,/2^j)$
. For
$\widehat {\Phi _j^{(m)}}(\vec {{\xi }}\,):=\widehat {\Phi ^{(m)}}(\vec {{\xi }}\,/2^j)$
. For
![]() $\gamma \in \mathbb {Z}$
, let
$\gamma \in \mathbb {Z}$
, let
and then we observe that
![]() $K^{\gamma }(\vec {{y}}\,)=2^{\gamma mn} K^0(2^{\gamma } \vec {{y}}\,)$
. For
$K^{\gamma }(\vec {{y}}\,)=2^{\gamma mn} K^0(2^{\gamma } \vec {{y}}\,)$
. For
![]() $\mu \in \mathbb {Z}$
, we define
$\mu \in \mathbb {Z}$
, we define
It follows from this definition that
which implies that
![]() $\widehat {K^{\gamma }_{\mu }}$
is bounded uniformly in
$\widehat {K^{\gamma }_{\mu }}$
is bounded uniformly in
![]() $\gamma $
, while they have almost disjoint supports, so it is natural to add them together as follows:
$\gamma $
, while they have almost disjoint supports, so it is natural to add them together as follows:
4.1 Reduction
We introduce the maximal operator
 $$ \begin{align*} {\mathcal{L}}_{\Omega}^{\sharp}\big(f_1,\dots,f_m\big)(x) := \sup_{\tau\in \mathbb Z} \bigg| \sum_{\gamma<\tau} \int_{(\mathbb R^n)^m }{K^{\gamma}(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \end{align*} $$
$$ \begin{align*} {\mathcal{L}}_{\Omega}^{\sharp}\big(f_1,\dots,f_m\big)(x) := \sup_{\tau\in \mathbb Z} \bigg| \sum_{\gamma<\tau} \int_{(\mathbb R^n)^m }{K^{\gamma}(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \end{align*} $$
for
![]() $x\in \mathbb R^n$
. Then we claim that
$x\in \mathbb R^n$
. Then we claim that
To prove (4.2), we introduce the notation
setting
![]() $\widehat {\Theta ^{(m)}}(\vec {{y}}\,):=1-\sum _{\gamma \in \mathbb {N}}{\widehat {\Phi ^{(m)}}(\vec {{y}}\,/2^{\gamma })}$
so that
$\widehat {\Theta ^{(m)}}(\vec {{y}}\,):=1-\sum _{\gamma \in \mathbb {N}}{\widehat {\Phi ^{(m)}}(\vec {{y}}\,/2^{\gamma })}$
so that
and
![]() $\widehat {\Theta ^{(m)}}(\vec {{y}}\,)=1$
for
$\widehat {\Theta ^{(m)}}(\vec {{y}}\,)=1$
for
![]() $|\vec {{y}}\,|\le 1$
.
$|\vec {{y}}\,|\le 1$
.
Given
![]() $\epsilon>0$
, choose
$\epsilon>0$
, choose
![]() $\rho \in \mathbb Z$
such that
$\rho \in \mathbb Z$
such that
![]() $2^{\rho }\le \epsilon <2^{\rho +1} $
. Then we write
$2^{\rho }\le \epsilon <2^{\rho +1} $
. Then we write
 $$ \begin{align} &\bigg| \int_{(\mathbb R^n)^m\setminus B(0,\epsilon)}{K(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \notag\\ &\qquad\qquad \le \bigg| \int_{(\mathbb R^n)^m }{\big( K^{(\epsilon)}(\vec{{y}}\,) - \widetilde{K}^{(2^{\rho})}(\vec{{y}}\,) \big) \prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \end{align} $$
$$ \begin{align} &\bigg| \int_{(\mathbb R^n)^m\setminus B(0,\epsilon)}{K(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \notag\\ &\qquad\qquad \le \bigg| \int_{(\mathbb R^n)^m }{\big( K^{(\epsilon)}(\vec{{y}}\,) - \widetilde{K}^{(2^{\rho})}(\vec{{y}}\,) \big) \prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \end{align} $$
 $$ \begin{align} &\qquad \qquad\qquad \qquad+ \bigg| \int_{(\mathbb R^n)^m} \widetilde{K}^{(2^{\rho})}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) ~d\,\vec{{y}}\,\bigg|. \end{align} $$
$$ \begin{align} &\qquad \qquad\qquad \qquad+ \bigg| \int_{(\mathbb R^n)^m} \widetilde{K}^{(2^{\rho})}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) ~d\,\vec{{y}}\,\bigg|. \end{align} $$
Term (4.4) is clearly less than
 $$ \begin{align*} \bigg|\sum_{\gamma\in\mathbb{Z}: \gamma<-\rho}\int_{(\mathbb R^n)^m}K^{\gamma}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) ~d\,\vec{{y}}\, \bigg|\le {\mathcal{L}}_{\Omega}^{\sharp}\big(f_1,\dots,f_m\big)(x), \end{align*} $$
$$ \begin{align*} \bigg|\sum_{\gamma\in\mathbb{Z}: \gamma<-\rho}\int_{(\mathbb R^n)^m}K^{\gamma}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) ~d\,\vec{{y}}\, \bigg|\le {\mathcal{L}}_{\Omega}^{\sharp}\big(f_1,\dots,f_m\big)(x), \end{align*} $$
while (4.3) is controlled by
![]() $ \mathcal {M}_{\Omega }\big (f_1,\dots ,f_m\big )(x) $
as
$ \mathcal {M}_{\Omega }\big (f_1,\dots ,f_m\big )(x) $
as
Thus, (4.2) follows after taking the supremum over all
![]() $\epsilon>0$
.
$\epsilon>0$
.
Since the boundedness of
![]() $\mathcal {M}_{\Omega }$
follows from Lemma 3.1 with the fact that
$\mathcal {M}_{\Omega }$
follows from Lemma 3.1 with the fact that
![]() $q>\frac {2m}{m+1}$
implies
$q>\frac {2m}{m+1}$
implies
![]() $\frac {m}{2} <\frac {1}{q}+\frac {m}{q'}$
, matters reduce to the boundedness of
$\frac {m}{2} <\frac {1}{q}+\frac {m}{q'}$
, matters reduce to the boundedness of
![]() ${\mathcal {L}}_{\Omega }^{\sharp }$
.
${\mathcal {L}}_{\Omega }^{\sharp }$
.
For each
![]() $\gamma \in \mathbb {Z}$
, let
$\gamma \in \mathbb {Z}$
, let
In the study of multilinear rough singular integral operators
![]() ${\mathcal {L}}_{\Omega }$
in [Reference Grafakos, He, Honzík and Park18] whose kernel is
${\mathcal {L}}_{\Omega }$
in [Reference Grafakos, He, Honzík and Park18] whose kernel is
![]() $\sum _{\gamma \in \mathbb {Z}}K^{\gamma }=\sum _{\mu \in \mathbb {Z}}\sum _{\gamma \in \mathbb {Z}}K_{\mu }^{\gamma }=\sum _{\mu \in \mathbb {Z}}K_{\mu }$
, the part where
$\sum _{\gamma \in \mathbb {Z}}K^{\gamma }=\sum _{\mu \in \mathbb {Z}}\sum _{\gamma \in \mathbb {Z}}K_{\mu }^{\gamma }=\sum _{\mu \in \mathbb {Z}}K_{\mu }$
, the part where
![]() $\mu $
is less than a constant is relatively simple because the Fourier transform of
$\mu $
is less than a constant is relatively simple because the Fourier transform of
![]() $K_{\mu }$
satisfies the estimate
$K_{\mu }$
satisfies the estimate
for all multi-indices
![]() $\alpha $
and
$\alpha $
and
![]() $\vec {{\xi }}\,\in \mathbb {R}^{mn}\setminus \{0\}$
, where
$\vec {{\xi }}\,\in \mathbb {R}^{mn}\setminus \{0\}$
, where
![]() $Q(\mu )=2^{(mn-\delta ')\mu }$
if
$Q(\mu )=2^{(mn-\delta ')\mu }$
if
![]() $\mu \ge 0$
and
$\mu \ge 0$
and
![]() $Q(\mu )=2^{\mu (1-\delta ')}$
if
$Q(\mu )=2^{\mu (1-\delta ')}$
if
![]() $\mu <0$
for some
$\mu <0$
for some
![]() $0<\delta '<1/q'$
, which is the condition of the Coifman–Meyer multiplier theorem ([Reference Coifman and Meyer9], [Reference Grafakos15, Theorem 7.5.3]) with constant
$0<\delta '<1/q'$
, which is the condition of the Coifman–Meyer multiplier theorem ([Reference Coifman and Meyer9], [Reference Grafakos15, Theorem 7.5.3]) with constant
![]() $\Vert \Omega \Vert _{L^q(\mathbb S^{mn-1})}Q(\mu )$
. The remaining case when
$\Vert \Omega \Vert _{L^q(\mathbb S^{mn-1})}Q(\mu )$
. The remaining case when
![]() $\mu $
is large enough was handled by using product-type wavelet decompositions. We expect that a similar strategy would work in handling
$\mu $
is large enough was handled by using product-type wavelet decompositions. We expect that a similar strategy would work in handling
![]() ${\mathcal {L}}_{\Omega }^{\sharp }$
.
${\mathcal {L}}_{\Omega }^{\sharp }$
.
To argue strictly, we write
where we set
 $$ \begin{align*}\widetilde {\mathcal{L}}_{\Omega}^{\sharp}\big(f_1,\dots,f_m\big) (x) := \sup_{\tau \in \mathbb Z} \bigg| \int_{(\mathbb R^n)^m }{ \sum_{ \gamma<\tau} \sum_{\mu\in\mathbb{Z}:2^{\mu-10}\le C_0\sqrt{mn}} K^{\gamma}_{\mu}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \end{align*} $$
$$ \begin{align*}\widetilde {\mathcal{L}}_{\Omega}^{\sharp}\big(f_1,\dots,f_m\big) (x) := \sup_{\tau \in \mathbb Z} \bigg| \int_{(\mathbb R^n)^m }{ \sum_{ \gamma<\tau} \sum_{\mu\in\mathbb{Z}:2^{\mu-10}\le C_0\sqrt{mn}} K^{\gamma}_{\mu}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg| \end{align*} $$
and
 $$ \begin{align*}{\mathcal{L}}_{\Omega,\mu}^{\sharp}\big(f_1,\dots,f_m\big)(x) := \sup_{\tau\in \mathbb Z} \bigg| \sum_{\gamma<\tau} \int_{(\mathbb R^n)^m }{ K^{\gamma}_{\mu}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg|. \end{align*} $$
$$ \begin{align*}{\mathcal{L}}_{\Omega,\mu}^{\sharp}\big(f_1,\dots,f_m\big)(x) := \sup_{\tau\in \mathbb Z} \bigg| \sum_{\gamma<\tau} \int_{(\mathbb R^n)^m }{ K^{\gamma}_{\mu}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j)}~d\,\vec{{y}}\, \bigg|. \end{align*} $$
Then Theorem 1.2 follows from the following two propositions.
Proposition 4.1 Let
![]() $1<p_1,\dots ,p_m\le \infty $
and
$1<p_1,\dots ,p_m\le \infty $
and
![]() $1/p=1/p_1+\cdots +1/p_m$
. Suppose that
$1/p=1/p_1+\cdots +1/p_m$
. Suppose that
![]() $1<q<\infty $
and
$1<q<\infty $
and
![]() $\Omega \in L^q(\mathbb {S}^{mn-1})$
with
$\Omega \in L^q(\mathbb {S}^{mn-1})$
with
![]() $\int _{\mathbb {S}^{mn-1}}\Omega d\sigma =0$
. Then there exists a constant
$\int _{\mathbb {S}^{mn-1}}\Omega d\sigma =0$
. Then there exists a constant
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align*} \big\Vert \widetilde{\mathcal{L}}_{\Omega}^{\sharp}(f_1,\dots,f_m)\big\Vert_{L^p}\le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^{p_j}} \end{align*} $$
$$ \begin{align*} \big\Vert \widetilde{\mathcal{L}}_{\Omega}^{\sharp}(f_1,\dots,f_m)\big\Vert_{L^p}\le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^{p_j}} \end{align*} $$
for Schwartz functions
![]() $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
Proposition 4.2 Let
![]() $\frac {2m}{m+1}<q\le \infty $
and
$\frac {2m}{m+1}<q\le \infty $
and
![]() $\Omega \in L^q(\mathbb {S}^{mn-1})$
with
$\Omega \in L^q(\mathbb {S}^{mn-1})$
with
![]() $\int _{\mathbb {S}^{mn-1}}\Omega d\sigma =0$
. Suppose that
$\int _{\mathbb {S}^{mn-1}}\Omega d\sigma =0$
. Suppose that
![]() $\mu \in \mathbb {Z}$
satisfies
$\mu \in \mathbb {Z}$
satisfies
![]() $2^{\mu -10}>C_0\sqrt {mn}$
. Then there exist
$2^{\mu -10}>C_0\sqrt {mn}$
. Then there exist
![]() $C, \epsilon _0>0$
such that
$C, \epsilon _0>0$
such that
 $$ \begin{align*} \big\| {\mathcal{L}}_{\Omega,\mu}^{\sharp}(f_1,\dots,f_m)\big\|_{L^{2/m} } \lesssim 2^{-\epsilon_0 \mu} \| \Omega\|_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} \end{align*} $$
$$ \begin{align*} \big\| {\mathcal{L}}_{\Omega,\mu}^{\sharp}(f_1,\dots,f_m)\big\|_{L^{2/m} } \lesssim 2^{-\epsilon_0 \mu} \| \Omega\|_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} \end{align*} $$
for Schwartz functions
![]() $f_1,\dots ,f_m$
on
$f_1,\dots ,f_m$
on
![]() $\mathbb R^n$
.
$\mathbb R^n$
.
4.2 Proof of Proposition 4.1
We decompose
![]() $\widetilde {\mathcal {L}}_{\Omega }^{\sharp }$
further so that the Coifman–Meyer multiplier theorem is involved: setting
$\widetilde {\mathcal {L}}_{\Omega }^{\sharp }$
further so that the Coifman–Meyer multiplier theorem is involved: setting
![]() $\widetilde {\mathcal {L}}^{\sharp }_{\Omega }\big (f_1,\dots ,f_m\big )(x)$
is controlled by the sum of
$\widetilde {\mathcal {L}}^{\sharp }_{\Omega }\big (f_1,\dots ,f_m\big )(x)$
is controlled by the sum of
 $$ \begin{align*} T_{\widetilde{K}}^*\big(f_1,\dots,f_m\big)(x):= \sup_{\tau\in\mathbb{Z}}\Big|\int_{|y|> 2^{-\tau}}\widetilde{K}(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)~d\,\vec{{y}}\, \Big| \end{align*} $$
$$ \begin{align*} T_{\widetilde{K}}^*\big(f_1,\dots,f_m\big)(x):= \sup_{\tau\in\mathbb{Z}}\Big|\int_{|y|> 2^{-\tau}}\widetilde{K}(\vec{{y}}\,)\prod_{j=1}^{m}f_j(x-y_j)~d\,\vec{{y}}\, \Big| \end{align*} $$
and
 $$ \begin{align} \mathfrak{T}_{K}^{**}\big(f_1,\dots,f_m\big)(x):= \sup_{\tau\in\mathbb{Z}}\Big| \int_{(\mathbb R^n)^m} {K}^{**}_{\tau}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) ~ d\,\vec{{y}}\, \Big|, \end{align} $$
$$ \begin{align} \mathfrak{T}_{K}^{**}\big(f_1,\dots,f_m\big)(x):= \sup_{\tau\in\mathbb{Z}}\Big| \int_{(\mathbb R^n)^m} {K}^{**}_{\tau}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) ~ d\,\vec{{y}}\, \Big|, \end{align} $$
where
 $$ \begin{align} {K}^{**}_{\tau}(\vec{{y}}\,):=\Big(\sum_{\mu\in\mathbb{Z}: 2^{\mu-10}\le C_0\sqrt{mn}}\; \sum_{\gamma<\tau}K_{\mu}^{\gamma}(\vec{{y}}\,)\Big) -\widetilde{K}(\vec{{y}}\,)\chi_{|\vec{{y}}\,|> 2^{-\tau}}. \end{align} $$
$$ \begin{align} {K}^{**}_{\tau}(\vec{{y}}\,):=\Big(\sum_{\mu\in\mathbb{Z}: 2^{\mu-10}\le C_0\sqrt{mn}}\; \sum_{\gamma<\tau}K_{\mu}^{\gamma}(\vec{{y}}\,)\Big) -\widetilde{K}(\vec{{y}}\,)\chi_{|\vec{{y}}\,|> 2^{-\tau}}. \end{align} $$
To obtain the boundedness of
![]() $T_{\widetilde {K}}^*$
, we claim that
$T_{\widetilde {K}}^*$
, we claim that
![]() $\widetilde {K}$
is an m-linear Calderón–Zygmund kernel with constant
$\widetilde {K}$
is an m-linear Calderón–Zygmund kernel with constant
![]() $C\Vert \Omega \Vert _{L^q(\mathbb {S}^{mn-1})}$
for
$C\Vert \Omega \Vert _{L^q(\mathbb {S}^{mn-1})}$
for
![]() $1<q< \infty $
. Indeed, it follows from (4.5) that
$1<q< \infty $
. Indeed, it follows from (4.5) that
 $$ \begin{align*} \big| \partial^{\alpha} \widehat{\widetilde{K}}(\vec{{\xi}}\,)\big|\le \sum_{\mu\in\mathbb{Z}: 2^{\mu-10}\le C_0\sqrt{mn}}\big|\partial^{\alpha}\widehat{K_{\mu}}(\vec{{\xi}}\,)\big|\lesssim \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}|\vec{{\xi}}\,|^{-|\alpha|} \end{align*} $$
$$ \begin{align*} \big| \partial^{\alpha} \widehat{\widetilde{K}}(\vec{{\xi}}\,)\big|\le \sum_{\mu\in\mathbb{Z}: 2^{\mu-10}\le C_0\sqrt{mn}}\big|\partial^{\alpha}\widehat{K_{\mu}}(\vec{{\xi}}\,)\big|\lesssim \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}|\vec{{\xi}}\,|^{-|\alpha|} \end{align*} $$
as the sum of
![]() $Q(\mu )$
over
$Q(\mu )$
over
![]() $\mu $
satisfying
$\mu $
satisfying
![]() $2^{\mu -10}\le C_0\sqrt {mn}$
converges. Then
$2^{\mu -10}\le C_0\sqrt {mn}$
converges. Then
![]() $\widetilde {K}$
satisfies the size and smoothness conditions for m-linear Calderón–Zygmund kernel with constant
$\widetilde {K}$
satisfies the size and smoothness conditions for m-linear Calderón–Zygmund kernel with constant
![]() $C\Vert \Omega \Vert _{L^q(\mathbb {S}^{mn-1})}$
, as mentioned in the proof of [Reference Grafakos and Torres21, Proposition 6]. Since
$C\Vert \Omega \Vert _{L^q(\mathbb {S}^{mn-1})}$
, as mentioned in the proof of [Reference Grafakos and Torres21, Proposition 6]. Since
![]() $\widetilde {K}$
is a Calderón–Zygmund kernel, Cotlar’s inequality in [Reference Grafakos and Torres20, Theorem 1] yields that
$\widetilde {K}$
is a Calderón–Zygmund kernel, Cotlar’s inequality in [Reference Grafakos and Torres20, Theorem 1] yields that
![]() $T_{\widetilde {K}}^*$
is bounded on the full range of exponents with constant
$T_{\widetilde {K}}^*$
is bounded on the full range of exponents with constant
![]() $C\Vert \Omega \Vert _{L^{q}(\mathbb {S}^{mn-1})}$
.
$C\Vert \Omega \Vert _{L^{q}(\mathbb {S}^{mn-1})}$
.
To handle the boundedness of the operator
![]() $\mathfrak {T}_K^{**}$
, we observe that the kernel
$\mathfrak {T}_K^{**}$
, we observe that the kernel
![]() ${K}_{\tau }^{**}$
can be written as
${K}_{\tau }^{**}$
can be written as
 $$ \begin{align} {K}_{\tau}^{**}(\vec{{y}}\,)=\sum_{\mu\in\mathbb{Z}:2^{\mu-10}\le C_0\sqrt{mn} }\; \Big( \sum_{\gamma<\tau}K_{\mu}^{\gamma}(\vec{{y}}\,)\chi_{|\vec{{y}}\,|\le 2^{-\tau}}- \sum_{\gamma\ge \tau}K_{\mu}^{\gamma}(\vec{{y}}\,)\chi_{|\vec{{y}}\,|>2^{-\tau}}\Big), \end{align} $$
$$ \begin{align} {K}_{\tau}^{**}(\vec{{y}}\,)=\sum_{\mu\in\mathbb{Z}:2^{\mu-10}\le C_0\sqrt{mn} }\; \Big( \sum_{\gamma<\tau}K_{\mu}^{\gamma}(\vec{{y}}\,)\chi_{|\vec{{y}}\,|\le 2^{-\tau}}- \sum_{\gamma\ge \tau}K_{\mu}^{\gamma}(\vec{{y}}\,)\chi_{|\vec{{y}}\,|>2^{-\tau}}\Big), \end{align} $$
and thus
where
 $$ \begin{align*} \mathcal{I}_{\mu,\tau}(x):= \sum_{\gamma<\tau}\Big|\int_{|\vec{{y}}\,|<2^{-\tau}} K_{\mu}^{\gamma}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) \;d\,\vec{{y}}\, \Big|, \end{align*} $$
$$ \begin{align*} \mathcal{I}_{\mu,\tau}(x):= \sum_{\gamma<\tau}\Big|\int_{|\vec{{y}}\,|<2^{-\tau}} K_{\mu}^{\gamma}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) \;d\,\vec{{y}}\, \Big|, \end{align*} $$
 $$ \begin{align*} \mathcal{J}_{\mu,\tau}(x):= \sum_{\gamma \ge \tau}\Big|\int_{|\vec{{y}}\,|\ge 2^{-\tau}} K_{\mu}^{\gamma}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) \;d\,\vec{{y}}\, \Big|. \end{align*} $$
$$ \begin{align*} \mathcal{J}_{\mu,\tau}(x):= \sum_{\gamma \ge \tau}\Big|\int_{|\vec{{y}}\,|\ge 2^{-\tau}} K_{\mu}^{\gamma}(\vec{{y}}\,) \prod_{j=1}^{m}f_j(x-y_j) \;d\,\vec{{y}}\, \Big|. \end{align*} $$
We claim that there exists
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
 $$ \begin{align} \mathcal{I}_{\mu,\tau}+ \mathcal{J}_{\mu,\tau}\lesssim_{C_0,m,n} 2^{\epsilon \mu}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\mathcal{M}f_j ~\text{ uniformly in ~} \tau\in\mathbb{Z} \end{align} $$
$$ \begin{align} \mathcal{I}_{\mu,\tau}+ \mathcal{J}_{\mu,\tau}\lesssim_{C_0,m,n} 2^{\epsilon \mu}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\mathcal{M}f_j ~\text{ uniformly in ~} \tau\in\mathbb{Z} \end{align} $$
for
![]() $\mu $
satisfying
$\mu $
satisfying
![]() $2^{\mu -10}\le C_0\sqrt {mn}$
, where we recall
$2^{\mu -10}\le C_0\sqrt {mn}$
, where we recall
![]() $\mathcal M$
is the Hardy–Littlewood maximal operator. Then, using Hölder’s inequality and the boundedness of
$\mathcal M$
is the Hardy–Littlewood maximal operator. Then, using Hölder’s inequality and the boundedness of
![]() $\mathcal {M}$
, we obtain
$\mathcal {M}$
, we obtain
 $$ \begin{align} \big\Vert \mathfrak{T}_{K}^{**}\big(f_1,\dots,f_m\big) \big\Vert_{L^p}\lesssim \Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})} \Big\Vert \prod_{j=1}^{m}\mathcal{M}f_j \Big\Vert_{L^p}\lesssim \Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^{p_j}} \end{align} $$
$$ \begin{align} \big\Vert \mathfrak{T}_{K}^{**}\big(f_1,\dots,f_m\big) \big\Vert_{L^p}\lesssim \Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})} \Big\Vert \prod_{j=1}^{m}\mathcal{M}f_j \Big\Vert_{L^p}\lesssim \Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^{p_j}} \end{align} $$
for
![]() $1<p_1,\dots ,p_m\le \infty $
and
$1<p_1,\dots ,p_m\le \infty $
and
![]() $0<p\le \infty $
satisfying
$0<p\le \infty $
satisfying
![]() $1/p=1/p_1+\dots +1/p_m$
as
$1/p=1/p_1+\dots +1/p_m$
as
![]() $\sum _{\mu : 2^{\mu -10}\le C_0\sqrt {mn}}2^{\epsilon \mu }$
converges. Therefore, let us prove (4.9).
$\sum _{\mu : 2^{\mu -10}\le C_0\sqrt {mn}}2^{\epsilon \mu }$
converges. Therefore, let us prove (4.9).
Using (4.1), we have
 $$ \begin{align*} \mathcal{I}_{\mu,\tau}(x)&\lesssim \sum_{\gamma<\tau}\int_{|\vec{{y}}\,|<2^{-\tau}}\int_{|\vec{{z}}\,|\approx 1}2^{\gamma mn}2^{\mu mn}|\Omega(\vec{{z}}\,')|d\vec{{z}}\, \prod_{j=1}^{m}|f_j(x-y_j)|~d\,\vec{{y}}\,\\ &\lesssim 2^{\mu mn}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\frac{1}{2^{-\tau mn}}\int_{|\vec{{y}}\,|<2^{-\tau}} \prod_{j=1}^{m}|f_j(x-y_j)| ~d\,\vec{{y}}\,\\ &\lesssim 2^{ \mu mn}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\mathcal{M}f_j(x), \end{align*} $$
$$ \begin{align*} \mathcal{I}_{\mu,\tau}(x)&\lesssim \sum_{\gamma<\tau}\int_{|\vec{{y}}\,|<2^{-\tau}}\int_{|\vec{{z}}\,|\approx 1}2^{\gamma mn}2^{\mu mn}|\Omega(\vec{{z}}\,')|d\vec{{z}}\, \prod_{j=1}^{m}|f_j(x-y_j)|~d\,\vec{{y}}\,\\ &\lesssim 2^{\mu mn}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\frac{1}{2^{-\tau mn}}\int_{|\vec{{y}}\,|<2^{-\tau}} \prod_{j=1}^{m}|f_j(x-y_j)| ~d\,\vec{{y}}\,\\ &\lesssim 2^{ \mu mn}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\mathcal{M}f_j(x), \end{align*} $$
as desired.
In addition,
 $$ \begin{align*} \mathcal{J}_{\mu,\tau}(x)\le \sum_{\gamma\ge \tau}\int_{|\vec{{y}}\,|\ge 2^{-\tau}}2^{\gamma mn}\Big|\int_{|\vec{{z}}\,|\approx 1}{\Phi_{\mu}(2^{\gamma}\vec{{y}}\,-\vec{{z}}\,)\Omega(\vec{{z}}\,')}d\,\vec{{z}}\, \Big|\prod_{j=1}^{m}|f_j(x-y_j)| ~ d\,\vec{{y}}\,. \end{align*} $$
$$ \begin{align*} \mathcal{J}_{\mu,\tau}(x)\le \sum_{\gamma\ge \tau}\int_{|\vec{{y}}\,|\ge 2^{-\tau}}2^{\gamma mn}\Big|\int_{|\vec{{z}}\,|\approx 1}{\Phi_{\mu}(2^{\gamma}\vec{{y}}\,-\vec{{z}}\,)\Omega(\vec{{z}}\,')}d\,\vec{{z}}\, \Big|\prod_{j=1}^{m}|f_j(x-y_j)| ~ d\,\vec{{y}}\,. \end{align*} $$
Since
![]() $\Omega $
has vanishing mean, we have
$\Omega $
has vanishing mean, we have
 $$ \begin{align*} &\Big|\int_{|\vec{{z}}\,|\approx 1}{\Phi_{\mu}(2^{\gamma}\vec{{y}}\,-\vec{{z}}\,)\,\Omega(\vec{{z}}\,')}\,d\,\vec{{z}}\, \Big| \\ &\lesssim 2^{\mu (mn+1)}\int_{|\vec{{z}}\,|\approx 1}\int_0^1\big| \nabla \Phi (2^{\mu+\gamma}\vec{{y}}\,-2^{\mu}t\vec{{z}}\,)\big|\;dt\; |\Omega(\vec{{z}}\,')|~ d\, \vec{{z}}\,. \end{align*} $$
$$ \begin{align*} &\Big|\int_{|\vec{{z}}\,|\approx 1}{\Phi_{\mu}(2^{\gamma}\vec{{y}}\,-\vec{{z}}\,)\,\Omega(\vec{{z}}\,')}\,d\,\vec{{z}}\, \Big| \\ &\lesssim 2^{\mu (mn+1)}\int_{|\vec{{z}}\,|\approx 1}\int_0^1\big| \nabla \Phi (2^{\mu+\gamma}\vec{{y}}\,-2^{\mu}t\vec{{z}}\,)\big|\;dt\; |\Omega(\vec{{z}}\,')|~ d\, \vec{{z}}\,. \end{align*} $$
Now we choose a constant M such that
![]() $mn<M<mn+1$
and see that
$mn<M<mn+1$
and see that
 $$ \begin{align*} \big| \nabla \Phi (2^{\mu+\gamma}\vec{{y}}\,-2^{\mu}t\vec{{z}}\,)\big|&\lesssim_M \frac{1}{(1+|2^{\mu+\gamma}\vec{{y}}\,-2^{\mu}t\vec{{z}}\,|)^M}\\ &\lesssim_{C_0,m,n,M} \frac{1}{(1+2^{\mu+\gamma}|\vec{{y}}\,|)^M}\le \frac{1}{2^{M(\mu+\gamma)}}\frac{1}{|\vec{{y}}\,|^{M}}, \end{align*} $$
$$ \begin{align*} \big| \nabla \Phi (2^{\mu+\gamma}\vec{{y}}\,-2^{\mu}t\vec{{z}}\,)\big|&\lesssim_M \frac{1}{(1+|2^{\mu+\gamma}\vec{{y}}\,-2^{\mu}t\vec{{z}}\,|)^M}\\ &\lesssim_{C_0,m,n,M} \frac{1}{(1+2^{\mu+\gamma}|\vec{{y}}\,|)^M}\le \frac{1}{2^{M(\mu+\gamma)}}\frac{1}{|\vec{{y}}\,|^{M}}, \end{align*} $$
as
![]() $|\vec {{z}}\,|\approx 1$
,
$|\vec {{z}}\,|\approx 1$
,
![]() $0<t<1$
, and
$0<t<1$
, and
![]() $2^{\mu -10}\le C_0\sqrt {mn}$
. This yields that
$2^{\mu -10}\le C_0\sqrt {mn}$
. This yields that
 $$ \begin{align*} \mathcal{J}_{\mu,\tau}(x)&\lesssim 2^{\mu(mn+1-M)}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\Big(\sum_{\gamma\ge \tau}2^{-\gamma(M- mn)}\Big)\\ &\qquad \qquad \qquad \qquad \times \int_{|\vec{{y}}\,|\ge 2^{-\tau}}{\frac{1}{|\vec{{y}}\,|^M}\prod_{j=1}^{m}|f_j(x-y_j)|}~ d\, \vec{{y}}\,. \end{align*} $$
$$ \begin{align*} \mathcal{J}_{\mu,\tau}(x)&\lesssim 2^{\mu(mn+1-M)}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\Big(\sum_{\gamma\ge \tau}2^{-\gamma(M- mn)}\Big)\\ &\qquad \qquad \qquad \qquad \times \int_{|\vec{{y}}\,|\ge 2^{-\tau}}{\frac{1}{|\vec{{y}}\,|^M}\prod_{j=1}^{m}|f_j(x-y_j)|}~ d\, \vec{{y}}\,. \end{align*} $$
Since
![]() $M>mn$
, the sum over
$M>mn$
, the sum over
![]() $\gamma \ge \tau $
converges to
$\gamma \ge \tau $
converges to
![]() $2^{-\tau (M-mn)}$
and the integral over
$2^{-\tau (M-mn)}$
and the integral over
![]() $|\vec {{y}}\,|\ge 2^{-\tau }$
is estimated by
$|\vec {{y}}\,|\ge 2^{-\tau }$
is estimated by
 $$ \begin{align*} &\sum_{l=0}^{\infty}\int_{2^{-\tau+l}\le |\vec{{y}}\,|<2^{-\tau+l+1}}{\frac{1}{|\vec{{y}}\,|^M}\prod_{j=1}^{m}|f_j(x-y_j)|}~ d\,\vec{{y}}\,\\ &\lesssim 2^{\tau(M-mn)}\sum_{l=0}^{\infty}2^{-l(M-mn)} \bigg(\frac{1}{2^{(-\tau+l+1)mn}}\int_{|\vec{{y}}\,|\le 2^{-\tau+l+1}}\prod_{j=1}^{m}|f_j(x-y_j)| ~ d\,\vec{{y}}\,\bigg)\\ &\lesssim 2^{\tau(M-mn)}\prod_{j=1}^{m}\mathcal{M}f_j(x). \end{align*} $$
$$ \begin{align*} &\sum_{l=0}^{\infty}\int_{2^{-\tau+l}\le |\vec{{y}}\,|<2^{-\tau+l+1}}{\frac{1}{|\vec{{y}}\,|^M}\prod_{j=1}^{m}|f_j(x-y_j)|}~ d\,\vec{{y}}\,\\ &\lesssim 2^{\tau(M-mn)}\sum_{l=0}^{\infty}2^{-l(M-mn)} \bigg(\frac{1}{2^{(-\tau+l+1)mn}}\int_{|\vec{{y}}\,|\le 2^{-\tau+l+1}}\prod_{j=1}^{m}|f_j(x-y_j)| ~ d\,\vec{{y}}\,\bigg)\\ &\lesssim 2^{\tau(M-mn)}\prod_{j=1}^{m}\mathcal{M}f_j(x). \end{align*} $$
Finally, we have
 $$ \begin{align*} \mathcal{J}_{\mu,\tau} \lesssim 2^{\mu(mn+1-M)}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\mathcal{M}f_j , \end{align*} $$
$$ \begin{align*} \mathcal{J}_{\mu,\tau} \lesssim 2^{\mu(mn+1-M)}\Vert \Omega\Vert_{L^1(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\mathcal{M}f_j , \end{align*} $$
which completes the proof of (4.9).
4.3 Proof of Proposition 4.2
The proof is based on the wavelet decomposition and the recent developments in [Reference Grafakos, He, Honzík and Park18]. Recalling that
![]() $\widehat {K_{\mu }^0}\in L^{q'}$
, we apply the wavelet decomposition (2.1) to write
$\widehat {K_{\mu }^0}\in L^{q'}$
, we apply the wavelet decomposition (2.1) to write
 $$ \begin{align*} \widehat{K_{\mu}^0}(\vec{{\xi}}\,)=\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in (\mathbb Z^n)^m}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots \Psi_{G_m,k_m}^{\lambda}(\xi_m), \end{align*} $$
$$ \begin{align*} \widehat{K_{\mu}^0}(\vec{{\xi}}\,)=\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in (\mathbb Z^n)^m}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots \Psi_{G_m,k_m}^{\lambda}(\xi_m), \end{align*} $$
where
It is known in [Reference Grafakos, He, Honzík and Park18] that for any
![]() $0<\delta <1/q'$
,
$0<\delta <1/q'$
,
where M is the number of vanishing moments of
![]() $\Psi _{\vec {{G}}}$
. Moreover, it follows from the inequality (2.2), the Hausdorff–Young inequality, and Young’s inequality that
$\Psi _{\vec {{G}}}$
. Moreover, it follows from the inequality (2.2), the Hausdorff–Young inequality, and Young’s inequality that
Now we may assume that
![]() $2^{\lambda +\mu -2}\le |\vec k|\le 2^{\lambda +\mu +2}$
due to the compact supports of
$2^{\lambda +\mu -2}\le |\vec k|\le 2^{\lambda +\mu +2}$
due to the compact supports of
![]() $\widehat {K_{\mu }^0}$
and
$\widehat {K_{\mu }^0}$
and
![]() $\Psi _{\vec {{G}},\vec {{k}}\,}^{\lambda }$
. In addition, by symmetry, it suffices to focus on the case
$\Psi _{\vec {{G}},\vec {{k}}\,}^{\lambda }$
. In addition, by symmetry, it suffices to focus on the case
![]() $|k_1|\ge \cdots \ge |k_m|$
. Since
$|k_1|\ge \cdots \ge |k_m|$
. Since
![]() $\widehat {K_{\mu }^{\gamma }}(\vec {{\xi }}\,)=\widehat {K_{\mu }^0}(\vec {{\xi }}\,/2^{\gamma })$
, the boundedness of
$\widehat {K_{\mu }^{\gamma }}(\vec {{\xi }}\,)=\widehat {K_{\mu }^0}(\vec {{\xi }}\,/2^{\gamma })$
, the boundedness of
![]() $ {\mathcal {L}}_{\Omega ,\mu }^{\sharp }$
is reduced to the inequality
$ {\mathcal {L}}_{\Omega ,\mu }^{\sharp }$
is reduced to the inequality
 $$ \begin{align} &\bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| \sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}} \sum_{\gamma\in\mathbb{Z}: \gamma<\tau}\sum_{\vec{{k}}\,\in\mathcal{U}^{\lambda+\mu}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\prod_{j=1}^{m} L_{G_j,k_j}^{\lambda,\gamma}f_j\Big|\bigg\Vert_{L^{2/m}}\nonumber\\ &\lesssim 2^{-\epsilon_0 \mu}\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align} $$
$$ \begin{align} &\bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| \sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}} \sum_{\gamma\in\mathbb{Z}: \gamma<\tau}\sum_{\vec{{k}}\,\in\mathcal{U}^{\lambda+\mu}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\prod_{j=1}^{m} L_{G_j,k_j}^{\lambda,\gamma}f_j\Big|\bigg\Vert_{L^{2/m}}\nonumber\\ &\lesssim 2^{-\epsilon_0 \mu}\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align} $$
where the operators
![]() $L_{G_j,k_j}^{\lambda ,\gamma }$
and the set
$L_{G_j,k_j}^{\lambda ,\gamma }$
and the set
![]() $\mathcal {U}^{\lambda +\mu }$
are defined as in (2.5) and (2.4). We split
$\mathcal {U}^{\lambda +\mu }$
are defined as in (2.5) and (2.4). We split
![]() $\mathcal {U}^{\lambda +{\mu }}$
into m disjoint subsets
$\mathcal {U}^{\lambda +{\mu }}$
into m disjoint subsets
![]() $\mathcal {U}_l^{\lambda +{\mu }}$
(
$\mathcal {U}_l^{\lambda +{\mu }}$
(
![]() $1\le l\le m$
) as before such that for
$1\le l\le m$
) as before such that for
![]() $k\in \mathcal {U}^{\lambda +\mu }_l$
, we have
$k\in \mathcal {U}^{\lambda +\mu }_l$
, we have
Then the left-hand side of (4.13) is estimated by
 $$ \begin{align*} \bigg( \sum_{l=1}^{m}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}} \bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| \sum_{\gamma\in\mathbb{Z}:\gamma<\tau} \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \Big| \bigg\Vert_{L^{2/m}}^{2/m}\bigg)^{m/2}, \end{align*} $$
$$ \begin{align*} \bigg( \sum_{l=1}^{m}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}} \bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| \sum_{\gamma\in\mathbb{Z}:\gamma<\tau} \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \Big| \bigg\Vert_{L^{2/m}}^{2/m}\bigg)^{m/2}, \end{align*} $$
where
![]() $\mathcal {T}_{\vec {{G}},l}^{\lambda ,\gamma ,\mu }$
is defined by
$\mathcal {T}_{\vec {{G}},l}^{\lambda ,\gamma ,\mu }$
is defined by
 $$ \begin{align*} \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}\big(f_1,\dots,f_m\big):=\sum_{\vec{{k}}\,\in\mathcal{U}_l^{\lambda+{\mu}}}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \bigg(\prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j \bigg). \end{align*} $$
$$ \begin{align*} \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}\big(f_1,\dots,f_m\big):=\sum_{\vec{{k}}\,\in\mathcal{U}_l^{\lambda+{\mu}}}b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \bigg(\prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_j \bigg). \end{align*} $$
We claim that for each
![]() $1\le l\le m$
, there exists
$1\le l\le m$
, there exists
![]() $\epsilon _0, M_0>0$
such that
$\epsilon _0, M_0>0$
such that
 $$ \begin{align} \begin{aligned} \bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| &\sum_{\gamma\in\mathbb{Z}:\gamma<\tau} \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \Big| \bigg\Vert_{L^{2/m}} \\ &\lesssim 2^{-\epsilon_0 \mu_0}2^{-\lambda M_0}\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| &\sum_{\gamma\in\mathbb{Z}:\gamma<\tau} \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \Big| \bigg\Vert_{L^{2/m}} \\ &\lesssim 2^{-\epsilon_0 \mu_0}2^{-\lambda M_0}\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{aligned} \end{align} $$
which concludes (4.13). Therefore, it remains to prove (4.14).
4.3.1 Proof of (4.14)
When
![]() $2\le l\le m$
, we apply (2.8) with
$2\le l\le m$
, we apply (2.8) with
![]() $2<q'<\frac {2m}{m-1}$
, along with (4.11), and (4.12) to obtain
$2<q'<\frac {2m}{m-1}$
, along with (4.11), and (4.12) to obtain
 $$ \begin{align*} &\bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| \sum_{\gamma\in\mathbb{Z}:\gamma<\tau}\mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}\big(f_1,\dots,f_m\big) \bigg\Vert_{L^{2/m}}\le \bigg\Vert \sum_{\gamma\in\mathbb{Z}} \big| \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}\big(f_1,\dots,f_m\big) \big| \bigg\Vert_{L^{2/m}} \\ &\lesssim \big\Vert \big\{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\big\}_{\vec{{k}}\,}\big\Vert_{\ell^{\infty}}^{1-\frac{(m-1)q'}{2m}} \big\Vert \big\{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\big\}_{\vec{{k}}\,}\big\Vert_{\ell^{q'}}^{\frac{(m-1)q'}{2m}} 2^{\lambda mn/2}(\lambda+1)^{l/2}{\mu}^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}\\ &\lesssim \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}2^{-\delta {\mu}(1-\frac{(m-1)q'}{2m})}{\mu}^{m/2}2^{-\lambda C_{M,m,n,q}}(\lambda+1)^{m/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} , \end{align*} $$
$$ \begin{align*} &\bigg\Vert \sup_{\tau\in\mathbb{Z}}\Big| \sum_{\gamma\in\mathbb{Z}:\gamma<\tau}\mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}\big(f_1,\dots,f_m\big) \bigg\Vert_{L^{2/m}}\le \bigg\Vert \sum_{\gamma\in\mathbb{Z}} \big| \mathcal{T}_{\vec{{G}},l}^{\lambda,\gamma,\mu}\big(f_1,\dots,f_m\big) \big| \bigg\Vert_{L^{2/m}} \\ &\lesssim \big\Vert \big\{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\big\}_{\vec{{k}}\,}\big\Vert_{\ell^{\infty}}^{1-\frac{(m-1)q'}{2m}} \big\Vert \big\{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\big\}_{\vec{{k}}\,}\big\Vert_{\ell^{q'}}^{\frac{(m-1)q'}{2m}} 2^{\lambda mn/2}(\lambda+1)^{l/2}{\mu}^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}\\ &\lesssim \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}2^{-\delta {\mu}(1-\frac{(m-1)q'}{2m})}{\mu}^{m/2}2^{-\lambda C_{M,m,n,q}}(\lambda+1)^{m/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} , \end{align*} $$
where
 $$ \begin{align*} C_{M,m,n,q}:=(M+1+mn)\bigg(1-\frac{(m-1)q'}{2m}\bigg)+mn(1/q-1/2)\frac{(m-1)q'}{2m}-\frac{mn}{2}. \end{align*} $$
$$ \begin{align*} C_{M,m,n,q}:=(M+1+mn)\bigg(1-\frac{(m-1)q'}{2m}\bigg)+mn(1/q-1/2)\frac{(m-1)q'}{2m}-\frac{mn}{2}. \end{align*} $$
Here, we used the fact that
![]() $\frac {l-1}{2l}\le \frac {m-1}{2m}$
for
$\frac {l-1}{2l}\le \frac {m-1}{2m}$
for
![]() $l\le m$
. Then (4.14) follows from choosing M sufficiently large so that
$l\le m$
. Then (4.14) follows from choosing M sufficiently large so that
![]() $C_{M,m,n,q}>0$
since
$C_{M,m,n,q}>0$
since
![]() $1-\frac {(m-1)q'}{2m}>0$
.
$1-\frac {(m-1)q'}{2m}>0$
.
Now let us prove (4.14) for
![]() $l=1$
. In this case, we first see the estimate
$l=1$
. In this case, we first see the estimate
 $$ \begin{align} \Big\Vert \Big( \sum_{\gamma\in\mathbb{Z}}\big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big|^2\Big)^{1/2}\Big\Vert_{L^{2/m}} \lesssim 2^{-\epsilon_0\mu} 2^{-M_0\lambda} \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} \end{align} $$
$$ \begin{align} \Big\Vert \Big( \sum_{\gamma\in\mathbb{Z}}\big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big|^2\Big)^{1/2}\Big\Vert_{L^{2/m}} \lesssim 2^{-\epsilon_0\mu} 2^{-M_0\lambda} \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} \end{align} $$
for some
![]() $\epsilon _0, M_0>0$
, which can be proved, as in [Reference Grafakos, He, Honzík and Park18, Section 6], by using (2.7) and (4.11).
$\epsilon _0, M_0>0$
, which can be proved, as in [Reference Grafakos, He, Honzík and Park18, Section 6], by using (2.7) and (4.11).
Choose a Schwartz function
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbb R^n$
whose Fourier transform is supported in the ball
$\mathbb R^n$
whose Fourier transform is supported in the ball
![]() $ \{\xi \in \mathbb R^n: |\xi |\le 2\}$
and is equal to
$ \{\xi \in \mathbb R^n: |\xi |\le 2\}$
and is equal to
![]() $1$
for
$1$
for
![]() $|\xi |\le 1$
, and define
$|\xi |\le 1$
, and define
![]() $\Gamma _k:=2^{kn}\Gamma (2^k\cdot )$
so that
$\Gamma _k:=2^{kn}\Gamma (2^k\cdot )$
so that
![]() $\mathrm {Supp}(\widehat {\Gamma _k})\subset \{\xi \in \mathbb R^n: |\xi |\le 2^{k+1}\}$
and
$\mathrm {Supp}(\widehat {\Gamma _k})\subset \{\xi \in \mathbb R^n: |\xi |\le 2^{k+1}\}$
and
![]() $\widehat {\Gamma _k}(\xi )=1$
for
$\widehat {\Gamma _k}(\xi )=1$
for
![]() $|\xi |\le 2^k$
.
$|\xi |\le 2^k$
.
Since the Fourier transform of
![]() $\mathcal {T}_{\vec {{G}},1}^{\lambda ,\gamma ,\mu }(f_1,\dots ,f_m)$
is supported in the set
$\mathcal {T}_{\vec {{G}},1}^{\lambda ,\gamma ,\mu }(f_1,\dots ,f_m)$
is supported in the set
![]() $\big \{ \xi \in \mathbb R^n: 2^{\gamma +\mu -5}\le |\xi |\le 2^{\gamma +\mu +4} \big \}$
, we can write
$\big \{ \xi \in \mathbb R^n: 2^{\gamma +\mu -5}\le |\xi |\le 2^{\gamma +\mu +4} \big \}$
, we can write
and then split the right-hand side into
Due to the Fourier support conditions of
![]() $\Gamma _{\tau +\mu +3}$
and
$\Gamma _{\tau +\mu +3}$
and
![]() $\mathcal {T}_{\vec {{G}},1}^{\lambda ,\gamma ,\mu }(f_1,\dots ,f_m)$
, the sum in the second term can be actually taken over
$\mathcal {T}_{\vec {{G}},1}^{\lambda ,\gamma ,\mu }(f_1,\dots ,f_m)$
, the sum in the second term can be actually taken over
![]() $\tau \le \gamma \le \tau +9$
. Therefore, the left-hand side of (4.14) is controlled by the sum of
$\tau \le \gamma \le \tau +9$
. Therefore, the left-hand side of (4.14) is controlled by the sum of
 $$ \begin{align} I:=\bigg\Vert \sup_{\nu\in\mathbb{Z}}\Big| \Gamma_{\nu}\ast \Big(\sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big)\Big| \bigg\Vert_{L^{2/m}} \end{align} $$
$$ \begin{align} I:=\bigg\Vert \sup_{\nu\in\mathbb{Z}}\Big| \Gamma_{\nu}\ast \Big(\sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big)\Big| \bigg\Vert_{L^{2/m}} \end{align} $$
and
 $$ \begin{align} II:=\sum_{\gamma=0}^{9}\Big\Vert \sup_{\tau\in\mathbb{Z}}\big| \Gamma_{\tau+\mu+3}\ast T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)\big|\Big\Vert_{L^{2/m}}. \end{align} $$
$$ \begin{align} II:=\sum_{\gamma=0}^{9}\Big\Vert \sup_{\tau\in\mathbb{Z}}\big| \Gamma_{\tau+\mu+3}\ast T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)\big|\Big\Vert_{L^{2/m}}. \end{align} $$
First of all, when
![]() $0\le \gamma \le 9$
, the Fourier supports of both
$0\le \gamma \le 9$
, the Fourier supports of both
![]() $\Gamma _{\tau +\mu +3}$
and
$\Gamma _{\tau +\mu +3}$
and
![]() $T_{\vec {{G}},1}^{\lambda ,\tau +\gamma ,\mu }(f_1,\dots ,f_m)$
are
$T_{\vec {{G}},1}^{\lambda ,\tau +\gamma ,\mu }(f_1,\dots ,f_m)$
are
![]() $\{\xi \in \mathbb R^n: |\xi |\sim 2^{\tau +\mu }\}$
. This implies that for any
$\{\xi \in \mathbb R^n: |\xi |\sim 2^{\tau +\mu }\}$
. This implies that for any
![]() $0<r<1$
,
$0<r<1$
,
 $$ \begin{align*} &\big| \Gamma_{\tau+\mu+3}\ast T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)(x)\big|\\ &\lesssim 2^{(\tau+\mu)(n/r-n)}\Big( \int_{\mathbb R^n} \big| \Gamma_{\tau+\mu+3}(x-y)\big|^r \big| T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)(y)\big|^r ~dy\Big)^{1/r}\\ &\lesssim \Big(\mathcal{M}\big(|T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)|^r\big)(x)\Big)^{1/r}, \end{align*} $$
$$ \begin{align*} &\big| \Gamma_{\tau+\mu+3}\ast T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)(x)\big|\\ &\lesssim 2^{(\tau+\mu)(n/r-n)}\Big( \int_{\mathbb R^n} \big| \Gamma_{\tau+\mu+3}(x-y)\big|^r \big| T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)(y)\big|^r ~dy\Big)^{1/r}\\ &\lesssim \Big(\mathcal{M}\big(|T_{\vec{{G}},1}^{\lambda,\tau+\gamma,\mu}(f_1,\dots,f_m)|^r\big)(x)\Big)^{1/r}, \end{align*} $$
where the Nikolskii inequality (see [Reference Triebel28, Proposition 1.3.2]) is applied in the first inequality. Setting
![]() $0<r<2/m$
, and using the maximal inequality for
$0<r<2/m$
, and using the maximal inequality for
![]() $\mathcal {M}$
and the embedding
$\mathcal {M}$
and the embedding
![]() $\ell ^2\hookrightarrow \ell ^{\infty }$
we obtain
$\ell ^2\hookrightarrow \ell ^{\infty }$
we obtain
 $$\begin{align*} &\le \Big\Vert \Big( \sum_{\gamma\in\mathbb{Z}}\big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big|^2\Big)^{1/2}\Big\Vert_{L^{2/m}}. \end{align*}$$
$$\begin{align*} &\le \Big\Vert \Big( \sum_{\gamma\in\mathbb{Z}}\big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big|^2\Big)^{1/2}\Big\Vert_{L^{2/m}}. \end{align*}$$
Then the
![]() $L^{2/m}$
norm is bounded by the right-hand side of (4.14), thanks to (4.15). This completes the estimate for
$L^{2/m}$
norm is bounded by the right-hand side of (4.14), thanks to (4.15). This completes the estimate for
![]() $II$
defined in (4.17), and we turn our attention to I defined in (4.16).
$II$
defined in (4.17), and we turn our attention to I defined in (4.16).
In the sequel, we will make use of the following inequality: if
![]() $\widehat {g_{\gamma }}$
is supported on
$\widehat {g_{\gamma }}$
is supported on
![]() $\{\xi \in \mathbb {R}^n : C^{-1} 2^{\gamma +\mu }\leq |\xi |\leq C2^{\gamma +\mu }\}$
for some
$\{\xi \in \mathbb {R}^n : C^{-1} 2^{\gamma +\mu }\leq |\xi |\leq C2^{\gamma +\mu }\}$
for some
![]() $C>1$
and
$C>1$
and
![]() $\mu \in \mathbb {Z}$
, then
$\mu \in \mathbb {Z}$
, then
for
![]() $0<p<\infty $
. The proof of (4.19) is elementary and standard, so it is omitted here (see [Reference Grafakos, He and Honzík16, equation (13)] and [Reference Yamazaki31, Theorem 3.6] for related arguments).
$0<p<\infty $
. The proof of (4.19) is elementary and standard, so it is omitted here (see [Reference Grafakos, He and Honzík16, equation (13)] and [Reference Yamazaki31, Theorem 3.6] for related arguments).
To obtain the bound of I, we note that
where
![]() $H^{2/m}$
is the Hardy space. We refer to [Reference Grafakos15, Corollary 2.1.8] for the above estimate. Then, using the Littlewood–Paley theory for Hardy space (see, for instance, [Reference Grafakos15, Theorem 2.2.9]) and (4.19), there exists a unique polynomial
$H^{2/m}$
is the Hardy space. We refer to [Reference Grafakos15, Corollary 2.1.8] for the above estimate. Then, using the Littlewood–Paley theory for Hardy space (see, for instance, [Reference Grafakos15, Theorem 2.2.9]) and (4.19), there exists a unique polynomial
![]() $Q^{\lambda ,\mu ,\vec {{G}}}(x)$
such that
$Q^{\lambda ,\mu ,\vec {{G}}}(x)$
such that
 $$ \begin{align} \Big\Vert \sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } -Q^{\lambda,\mu,\vec{{G}}} \Big\Vert_{H^{2/m}}\notag &\lesssim \Big\Vert \Big( \sum_{\gamma\in\mathbb{Z}}\big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big|^2\Big)^{1/2}\Big\Vert_{L^{2/m}}\nonumber\\ & \lesssim 2^{-\epsilon_0\mu} 2^{-M_0\lambda} \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align} $$
$$ \begin{align} \Big\Vert \sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } -Q^{\lambda,\mu,\vec{{G}}} \Big\Vert_{H^{2/m}}\notag &\lesssim \Big\Vert \Big( \sum_{\gamma\in\mathbb{Z}}\big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big|^2\Big)^{1/2}\Big\Vert_{L^{2/m}}\nonumber\\ & \lesssim 2^{-\epsilon_0\mu} 2^{-M_0\lambda} \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align} $$
where (4.15) is applied. Furthermore,
 $$ \begin{align*} &\Big\Vert \sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big\Vert_{H^{2/m}}\\ &\approx \bigg\Vert \sup_{\nu\in\mathbb{Z}}\Big|\Gamma_{\nu}\ast\Big( \sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big)\Big|\bigg\Vert_{L^{2/m}}\\ &=\bigg\Vert \sup_{\nu\in\mathbb{Z}}\Big|\Gamma_{\nu}\ast\Big( \sum_{\gamma\in\mathbb{Z}: \gamma\le \nu-\mu+5}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big)\Big|\bigg\Vert_{L^{2/m}}\\ &\lesssim \bigg\Vert \sup_{\nu\in\mathbb{Z}} \Big| \sum_{\gamma\in\mathbb{Z}: \gamma\le \nu-\mu+5}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) }\Big|\bigg\Vert_{L^{2/m}}\\ &\le \Big\Vert \sum_{\gamma\in\mathbb{Z}}{ \big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big| }\Big\Vert_{L^{2/m}}, \end{align*} $$
$$ \begin{align*} &\Big\Vert \sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big\Vert_{H^{2/m}}\\ &\approx \bigg\Vert \sup_{\nu\in\mathbb{Z}}\Big|\Gamma_{\nu}\ast\Big( \sum_{\gamma\in\mathbb{Z}}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big)\Big|\bigg\Vert_{L^{2/m}}\\ &=\bigg\Vert \sup_{\nu\in\mathbb{Z}}\Big|\Gamma_{\nu}\ast\Big( \sum_{\gamma\in\mathbb{Z}: \gamma\le \nu-\mu+5}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) } \Big)\Big|\bigg\Vert_{L^{2/m}}\\ &\lesssim \bigg\Vert \sup_{\nu\in\mathbb{Z}} \Big| \sum_{\gamma\in\mathbb{Z}: \gamma\le \nu-\mu+5}{ \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) }\Big|\bigg\Vert_{L^{2/m}}\\ &\le \Big\Vert \sum_{\gamma\in\mathbb{Z}}{ \big| \mathcal{T}_{\vec{{G}},1}^{\lambda,\gamma,\mu}(f_1,\dots,f_m) \big| }\Big\Vert_{L^{2/m}}, \end{align*} $$
where the argument that led to (4.18) is applied in the first inequality. As we have discussed in [Reference Grafakos, He, Honzík and Park18, Section 6.1], this quantity is finite for all Schwartz functions
![]() $f_1,\dots ,f_m$
. Accordingly, we have
$f_1,\dots ,f_m$
. Accordingly, we have
and
and thus
![]() $Q^{\lambda ,\mu ,\vec {{G}}}=0$
. Now it follows from (4.20) that
$Q^{\lambda ,\mu ,\vec {{G}}}=0$
. Now it follows from (4.20) that
 $$ \begin{align*} I \lesssim 2^{-\epsilon_0\mu} 2^{-M_0\lambda} \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align*} $$
$$ \begin{align*} I \lesssim 2^{-\epsilon_0\mu} 2^{-M_0\lambda} \Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align*} $$
as expected. This completes the proof of (4.14).
5 Proof of Theorem 1.1
We now prove Theorem 1.1 by making use of Theorem 1.2. Recall that in Theorem 1.2 we established the boundedness only for Schwartz functions. An important obstacle we address is the pointwise definition of the maximal operator
![]() $\mathcal L^{**}$
(see (1.3)) for general
$\mathcal L^{**}$
(see (1.3)) for general
![]() $L^2$
functions. This definition can be given via an abstract extension (see [Reference Dosidis and Grafakos11]), but this is not as useful for our purposes. We provide below a concrete approach that preserves the pointwise bounds provided by the supremum.
$L^2$
functions. This definition can be given via an abstract extension (see [Reference Dosidis and Grafakos11]), but this is not as useful for our purposes. We provide below a concrete approach that preserves the pointwise bounds provided by the supremum.
5.1 A variant of Theorem 1.2 for general
 $L^2$
functions
$L^2$
functions
We note that when
![]() $f_j\in L^{2}(\mathbb {R}^n)$
, by Lemma 3.1, there exists a set
$f_j\in L^{2}(\mathbb {R}^n)$
, by Lemma 3.1, there exists a set
![]() $E^{\Omega }_{f_1,\dots , f_m}$
of measure
$E^{\Omega }_{f_1,\dots , f_m}$
of measure
![]() $0$
such that
$0$
such that
when
![]() $x\notin E^{\Omega }_{f_1,\dots , f_m}$
. Therefore, for
$x\notin E^{\Omega }_{f_1,\dots , f_m}$
. Therefore, for
![]() $x\notin E^{\Omega }_{f_1,\dots , f_m}$
, we have
$x\notin E^{\Omega }_{f_1,\dots , f_m}$
, we have
 $$ \begin{align} \int_{\epsilon_0 \le |\vec{{y}}\,| \le \epsilon_0^{-1}} \frac{|\Omega (\vec{{y}}\,')|}{|\vec{{y}}\,|^{mn}}\, \prod_{j=1}^{m}\big|f_j(x-y_j)\big|\; d\vec{{y}}\, \le C \frac{1 }{\epsilon_0^{2mn}} \mathcal M_{\Omega} \big(f_1,\dots , f_m\big)(x), \end{align} $$
$$ \begin{align} \int_{\epsilon_0 \le |\vec{{y}}\,| \le \epsilon_0^{-1}} \frac{|\Omega (\vec{{y}}\,')|}{|\vec{{y}}\,|^{mn}}\, \prod_{j=1}^{m}\big|f_j(x-y_j)\big|\; d\vec{{y}}\, \le C \frac{1 }{\epsilon_0^{2mn}} \mathcal M_{\Omega} \big(f_1,\dots , f_m\big)(x), \end{align} $$
and thus
![]() ${\mathcal {L}}_{\Omega }^{ ( \epsilon , \epsilon ^{-1}) }(f_1,\dots , f_m)(x)$
and
${\mathcal {L}}_{\Omega }^{ ( \epsilon , \epsilon ^{-1}) }(f_1,\dots , f_m)(x)$
and
![]() ${\mathcal {L}}_{\Omega }^{*, \epsilon _0 }(f_1,\dots , f_m)(x)$
are well defined, for
${\mathcal {L}}_{\Omega }^{*, \epsilon _0 }(f_1,\dots , f_m)(x)$
are well defined, for
![]() $f_j$
in
$f_j$
in
![]() $L^2(\mathbb {R}^n)$
and
$L^2(\mathbb {R}^n)$
and
![]() $\Omega $
in
$\Omega $
in
![]() $L^q(\mathbb {S}^{mn-1})$
. Moreover,
$L^q(\mathbb {S}^{mn-1})$
. Moreover,
pointwise for
![]() $x\in \mathbb R^n\setminus E_{f_1,\dots , f_m}^{\Omega }$
.
$x\in \mathbb R^n\setminus E_{f_1,\dots , f_m}^{\Omega }$
.
For given
![]() $f_j\in L^2(\mathbb {R}^n)$
, we pick sequences of Schwartz functions
$f_j\in L^2(\mathbb {R}^n)$
, we pick sequences of Schwartz functions
![]() $f_j^k$
converging to
$f_j^k$
converging to
![]() $f_j$
in
$f_j$
in
![]() $L^2$
as
$L^2$
as
![]() $k\to \infty $
, by density. Using the identity
$k\to \infty $
, by density. Using the identity
 $$ \begin{align} a_1a_2\cdots a_m - b_1b_2\cdots b_m= \sum_{j=1}^m b_1 \cdots b_{j-1} (a_j-b_j) a_{j+1}\cdots a_m \end{align} $$
$$ \begin{align} a_1a_2\cdots a_m - b_1b_2\cdots b_m= \sum_{j=1}^m b_1 \cdots b_{j-1} (a_j-b_j) a_{j+1}\cdots a_m \end{align} $$
(with the obvious modification when
![]() $j=1$
or
$j=1$
or
![]() $j=m$
), the inequality
$j=m$
), the inequality
 $$\begin{align*}{\mathcal{L}}_{\Omega}^{*,\epsilon_0 }\big(f_1,\dots , f_m\big)\le 2{\mathcal{L}}_{\Omega}^{*}(f_1^k,\dots , f_m^k) +\sum_{j=1}^m {\mathcal{L}}_{\Omega}^{*,\epsilon_0 }(f_1^k,\dots f_{j-1}^k, f_j-f_j^k, f_{j+1}\dots , f_m ) \end{align*}$$
$$\begin{align*}{\mathcal{L}}_{\Omega}^{*,\epsilon_0 }\big(f_1,\dots , f_m\big)\le 2{\mathcal{L}}_{\Omega}^{*}(f_1^k,\dots , f_m^k) +\sum_{j=1}^m {\mathcal{L}}_{\Omega}^{*,\epsilon_0 }(f_1^k,\dots f_{j-1}^k, f_j-f_j^k, f_{j+1}\dots , f_m ) \end{align*}$$
is valid pointwise on the complement of the set
 $$ \begin{align} E^{\Omega}:=E_{f_1,\dots, f_m}^{\Omega} \cup \left( \bigcup_{k=1}^{\infty} E_{f_1^k,\dots, f_m^k}^{\Omega}\right) \cup \bigg( \bigcup_{j=1}^m\bigcup_{k=1}^{\infty} E_{f_1^k,\dots f_{j-1}^k, f_j-f_j^k, f_{j+1}\dots , f_m }^{\Omega} \bigg), \end{align} $$
$$ \begin{align} E^{\Omega}:=E_{f_1,\dots, f_m}^{\Omega} \cup \left( \bigcup_{k=1}^{\infty} E_{f_1^k,\dots, f_m^k}^{\Omega}\right) \cup \bigg( \bigcup_{j=1}^m\bigcup_{k=1}^{\infty} E_{f_1^k,\dots f_{j-1}^k, f_j-f_j^k, f_{j+1}\dots , f_m }^{\Omega} \bigg), \end{align} $$
which is a set of measure zero. Now we take the
![]() $L^{2/m} $
quasi-norm on both sides and apply Theorem 1.3 for Schwartz functions and the estimate (5.1), combined with Lemma 3.1, for the terms in the sum. Taking
$L^{2/m} $
quasi-norm on both sides and apply Theorem 1.3 for Schwartz functions and the estimate (5.1), combined with Lemma 3.1, for the terms in the sum. Taking
![]() $k\to \infty $
, we obtain
$k\to \infty $
, we obtain
 $$ \begin{align*} \big\|{\mathcal{L}}_{\Omega}^{*,\epsilon_0 }(f_1,\dots , f_m)\big\|_{L^{2/m}(\mathbb{R}^n) } \le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})} \prod_{j=1}^{\infty}\| f_j\|_{L^{2}(\mathbb{R}^n)}. \end{align*} $$
$$ \begin{align*} \big\|{\mathcal{L}}_{\Omega}^{*,\epsilon_0 }(f_1,\dots , f_m)\big\|_{L^{2/m}(\mathbb{R}^n) } \le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})} \prod_{j=1}^{\infty}\| f_j\|_{L^{2}(\mathbb{R}^n)}. \end{align*} $$
Finally, letting
![]() $\epsilon _0 \to 0$
and using the monotone convergence theorem, we conclude
$\epsilon _0 \to 0$
and using the monotone convergence theorem, we conclude
 $$ \begin{align} \big\|{\mathcal{L}}_{\Omega}^{** }(f_1,\dots , f_m)\big\|_{L^{2/m}(\mathbb{R}^n) } \le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})} \prod_{j=1}^{\infty}\| f_j\|_{L^{2}(\mathbb{R}^n)} \end{align} $$
$$ \begin{align} \big\|{\mathcal{L}}_{\Omega}^{** }(f_1,\dots , f_m)\big\|_{L^{2/m}(\mathbb{R}^n) } \le C\Vert \Omega\Vert_{L^q(\mathbb{S}^{mn-1})} \prod_{j=1}^{\infty}\| f_j\|_{L^{2}(\mathbb{R}^n)} \end{align} $$
for
![]() $f_j\in L^2(\mathbb {R}^n)$
.
$f_j\in L^2(\mathbb {R}^n)$
.
5.2 Proof of Theorem 1.1
Let
![]() $f_1,\dots ,f_m$
be given
$f_1,\dots ,f_m$
be given
![]() $L^2$
functions and pick sequences
$L^2$
functions and pick sequences
![]() $\{f_j^k\}$
of Schwartz functions such that
$\{f_j^k\}$
of Schwartz functions such that
![]() $f_j^k$
converges to
$f_j^k$
converges to
![]() $f_j$
in
$f_j$
in
![]() $L^2(\mathbb {R}^n)$
as
$L^2(\mathbb {R}^n)$
as
![]() $k\to \infty $
. Recall that
$k\to \infty $
. Recall that
![]() ${\mathcal {L}}_{\Omega }(f_1 ,\dots , f_m )$
is defined as the
${\mathcal {L}}_{\Omega }(f_1 ,\dots , f_m )$
is defined as the
![]() $L^{2/m}$
limit of
$L^{2/m}$
limit of
![]() ${\mathcal {L}}_{\Omega }(f_1^k ,\dots , f_m^k )$
as
${\mathcal {L}}_{\Omega }(f_1^k ,\dots , f_m^k )$
as
![]() $k\to \infty $
. Then there exists a subsequence
$k\to \infty $
. Then there exists a subsequence
![]() $\{k_l\}$
of
$\{k_l\}$
of
![]() $\{k\}$
such that
$\{k\}$
such that
![]() ${\mathcal {L}}_{\Omega }(f_1^{k_l} ,\dots , f_m^{k_l} ) \to {\mathcal {L}}_{\Omega }(f_1 ,\dots , f_m )$
pointwise on
${\mathcal {L}}_{\Omega }(f_1^{k_l} ,\dots , f_m^{k_l} ) \to {\mathcal {L}}_{\Omega }(f_1 ,\dots , f_m )$
pointwise on
![]() $\mathbb R^n\setminus E$
, for some set E of measure zero. Let us denote the subsequence
$\mathbb R^n\setminus E$
, for some set E of measure zero. Let us denote the subsequence
![]() $\{k_l\}$
still by
$\{k_l\}$
still by
![]() $\{k\}$
for notational convenience. Then, on
$\{k\}$
for notational convenience. Then, on
![]() $\mathbb R^n\setminus (E\cup E^{\Omega })$
, where
$\mathbb R^n\setminus (E\cup E^{\Omega })$
, where
![]() $E^{\Omega }$
is as in (5.3), we have
$E^{\Omega }$
is as in (5.3), we have
 $$ \begin{align*} \big|{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}&(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m )\big|\\ &\le \big|{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1^k ,\dots, f_m^k )\big|\\ & \quad + \big| {\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1^k ,\dots, f_m^k ) - {\mathcal{L}}_{\Omega} (f_1^k ,\dots, f_m^k ) \big|\\ & \quad \quad + \big| {\mathcal{L}}_{\Omega} (f_1^k ,\dots, f_m^k ) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m ) \big|. \end{align*} $$
$$ \begin{align*} \big|{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}&(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m )\big|\\ &\le \big|{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1^k ,\dots, f_m^k )\big|\\ & \quad + \big| {\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1^k ,\dots, f_m^k ) - {\mathcal{L}}_{\Omega} (f_1^k ,\dots, f_m^k ) \big|\\ & \quad \quad + \big| {\mathcal{L}}_{\Omega} (f_1^k ,\dots, f_m^k ) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m ) \big|. \end{align*} $$
We first take the
![]() $\limsup _{\epsilon \to 0}$
on both sides and then the middle term on the right vanishes. Then we apply
$\limsup _{\epsilon \to 0}$
on both sides and then the middle term on the right vanishes. Then we apply
![]() $\liminf _{k\to \infty }$
so that the last term vanishes. Consequently, we have
$\liminf _{k\to \infty }$
so that the last term vanishes. Consequently, we have
 $$ \begin{align*} \limsup_{\epsilon \to 0}|&{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m )|\\ &\le \liminf_{k\to \infty} \sum_{j=1}^m {\mathcal{L}}_{\Omega}^{**} (f_1,\dots, f_{j-1} , f_j-f_j^k, f_{j+1}^k, \dots , f_m^k) \end{align*} $$
$$ \begin{align*} \limsup_{\epsilon \to 0}|&{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m )|\\ &\le \liminf_{k\to \infty} \sum_{j=1}^m {\mathcal{L}}_{\Omega}^{**} (f_1,\dots, f_{j-1} , f_j-f_j^k, f_{j+1}^k, \dots , f_m^k) \end{align*} $$
on
![]() $\mathbb R^n\setminus \big (E\cup E^{\Omega }\big )$
, where the identity (5.2) is applied. It follows that
$\mathbb R^n\setminus \big (E\cup E^{\Omega }\big )$
, where the identity (5.2) is applied. It follows that
 $$ \begin{align*} & \Big|\big\{x:\,\,\limsup_{\epsilon \to 0}|{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m )|>\lambda\big\}\Big| \\ &\le \Big|\big\{x:\,\, \liminf_{k\to \infty} \sum_{j=1}^m {\mathcal{L}}_{\Omega}^{**} (f_1,\dots, f_{j-1} , f_j-f_j^k, f_{j+1}^k, \dots , f_m^k)>\lambda\big\}\Big| \\ &\le \lambda^{-\frac 2m} \sum_{j=1}^m \Big\| \liminf_{k\to \infty} \sum_{j=1}^m {\mathcal{L}}_{\Omega}^{**} (f_1,\dots, f_{j-1} , f_j-f_j^k, f_{j+1}^k, \dots , f_m^k)\big\|_{L^{\frac 2m}}^{\frac 2m} \end{align*} $$
$$ \begin{align*} & \Big|\big\{x:\,\,\limsup_{\epsilon \to 0}|{\mathcal{L}}_{\Omega}^{(\epsilon,\epsilon^{-1})}(f_1,\dots, f_m) -{\mathcal{L}}_{\Omega}(f_1 ,\dots, f_m )|>\lambda\big\}\Big| \\ &\le \Big|\big\{x:\,\, \liminf_{k\to \infty} \sum_{j=1}^m {\mathcal{L}}_{\Omega}^{**} (f_1,\dots, f_{j-1} , f_j-f_j^k, f_{j+1}^k, \dots , f_m^k)>\lambda\big\}\Big| \\ &\le \lambda^{-\frac 2m} \sum_{j=1}^m \Big\| \liminf_{k\to \infty} \sum_{j=1}^m {\mathcal{L}}_{\Omega}^{**} (f_1,\dots, f_{j-1} , f_j-f_j^k, f_{j+1}^k, \dots , f_m^k)\big\|_{L^{\frac 2m}}^{\frac 2m} \end{align*} $$
by Chebyshev’s inequality. But this last expression tends to zero as
![]() $k\to \infty $
in view of Fatou’s lemma and (5.4). We conclude that
$k\to \infty $
in view of Fatou’s lemma and (5.4). We conclude that
equals zero a.e. and this finishes the proof.
6 Proof of Theorem 1.4
Let
![]() $\mu _0$
be the smallest integer satisfying
$\mu _0$
be the smallest integer satisfying
![]() $2^{{\mu }_0-3}>C_0\sqrt {mn}$
and
$2^{{\mu }_0-3}>C_0\sqrt {mn}$
and
 $$ \begin{align*}\widehat{\Theta^{(m)}_{{\mu}_0-1}}(\vec{{\xi}}\,):=1-\sum_{{\mu}={\mu}_0}^{\infty}{\widehat{\Phi_{\mu}^{(m)}}(\vec{{\xi}}\,)}.\end{align*} $$
$$ \begin{align*}\widehat{\Theta^{(m)}_{{\mu}_0-1}}(\vec{{\xi}}\,):=1-\sum_{{\mu}={\mu}_0}^{\infty}{\widehat{\Phi_{\mu}^{(m)}}(\vec{{\xi}}\,)}.\end{align*} $$
Clearly,
 $$ \begin{align*} \widehat{\Theta^{(m)}_{{\mu}_0-1}}(\vec{{\xi}}\,)+\sum_{{\mu}={\mu}_0}^{\infty}{\widehat{\Phi_{\mu}^{(m)}}(\vec{{\xi}}\,)}=1, \end{align*} $$
$$ \begin{align*} \widehat{\Theta^{(m)}_{{\mu}_0-1}}(\vec{{\xi}}\,)+\sum_{{\mu}={\mu}_0}^{\infty}{\widehat{\Phi_{\mu}^{(m)}}(\vec{{\xi}}\,)}=1, \end{align*} $$
and thus we can write
 $$ \begin{align*} \sigma(\vec{{\xi}}\,)=\widehat{\Theta_{{\mu}_0-1}^{(m)}}(\vec{{\xi}}\,)\sigma(\vec{{\xi}}\,)+\sum_{{\mu}={\mu}_0}^{\infty}{\widehat{\Phi_{\mu}^{(m)}}(\vec{{\xi}}\,)\sigma(\vec{{\xi}}\,)}=:\sigma_{{\mu}_0-1}(\vec{{\xi}}\,)+\sum_{{\mu}={\mu}_0}^{\infty}{\sigma_{\mu}(\vec{{\xi}}\,)}. \end{align*} $$
$$ \begin{align*} \sigma(\vec{{\xi}}\,)=\widehat{\Theta_{{\mu}_0-1}^{(m)}}(\vec{{\xi}}\,)\sigma(\vec{{\xi}}\,)+\sum_{{\mu}={\mu}_0}^{\infty}{\widehat{\Phi_{\mu}^{(m)}}(\vec{{\xi}}\,)\sigma(\vec{{\xi}}\,)}=:\sigma_{{\mu}_0-1}(\vec{{\xi}}\,)+\sum_{{\mu}={\mu}_0}^{\infty}{\sigma_{\mu}(\vec{{\xi}}\,)}. \end{align*} $$
Note that
![]() $\sigma _{{\mu }_0-1}$
is a compactly supported smooth function and thus the corresponding maximal multiplier operator
$\sigma _{{\mu }_0-1}$
is a compactly supported smooth function and thus the corresponding maximal multiplier operator
![]() $\mathscr {M}_{\sigma _{{\mu }_0-1}}$
, defined by
$\mathscr {M}_{\sigma _{{\mu }_0-1}}$
, defined by
 $$ \begin{align*} &\mathscr{M}_{\sigma_{{\mu}_0-1}}\big(f_1,\dots,f_m\big)(x)\\ &:=\sup_{\nu \in\mathbb{Z}}\Big|\int_{(\mathbb R^n)^m}{\sigma_{{\mu}_0-1}(2^{\nu} \vec{{\xi}}\,)\bigg( \prod_{j=1}^{m}\widehat{f_j}(\xi_j)\bigg) e^{2\pi i\langle x,\sum_{j=1}^{m}\xi_j \rangle}}d\vec{{\xi}}\, \Big|, \end{align*} $$
$$ \begin{align*} &\mathscr{M}_{\sigma_{{\mu}_0-1}}\big(f_1,\dots,f_m\big)(x)\\ &:=\sup_{\nu \in\mathbb{Z}}\Big|\int_{(\mathbb R^n)^m}{\sigma_{{\mu}_0-1}(2^{\nu} \vec{{\xi}}\,)\bigg( \prod_{j=1}^{m}\widehat{f_j}(\xi_j)\bigg) e^{2\pi i\langle x,\sum_{j=1}^{m}\xi_j \rangle}}d\vec{{\xi}}\, \Big|, \end{align*} $$
is bounded by a constant multiple of
![]() $ \mathcal {M}f_1(x)\cdots \mathcal {M}f_m(x), $
where
$ \mathcal {M}f_1(x)\cdots \mathcal {M}f_m(x), $
where
![]() $\mathcal {M}$
is the Hardy–Littlewood maximal operator on
$\mathcal {M}$
is the Hardy–Littlewood maximal operator on
![]() $\mathbb R^n$
as before. Using Hölder’s inequality and the
$\mathbb R^n$
as before. Using Hölder’s inequality and the
![]() $L^2$
-boundedness of
$L^2$
-boundedness of
![]() $\mathcal {M}$
, we can prove
$\mathcal {M}$
, we can prove
 $$ \begin{align*} \big\Vert \mathscr{M}_{\sigma_{{\mu}_0-1}}(f_1,\dots,f_m) \big\Vert_{L^{2/m}}\lesssim \prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align*} $$
$$ \begin{align*} \big\Vert \mathscr{M}_{\sigma_{{\mu}_0-1}}(f_1,\dots,f_m) \big\Vert_{L^{2/m}}\lesssim \prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align*} $$
It remains to show that
 $$ \begin{align} \Big\Vert \sum_{{\mu}={\mu}_0}^{\infty}\mathscr{M}_{\sigma_{\mu}}(f_1,\dots,f_m)\Big\Vert_{L^{2/m}}\lesssim \prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align} $$
$$ \begin{align} \Big\Vert \sum_{{\mu}={\mu}_0}^{\infty}\mathscr{M}_{\sigma_{\mu}}(f_1,\dots,f_m)\Big\Vert_{L^{2/m}}\lesssim \prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align} $$
Using the decomposition (2.1), write
 $$ \begin{align} \sigma_{\mu}(\vec{{\xi}}\,)=\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in (\mathbb Z^n)^m}{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots\Psi_{G_m,k_m}^{\lambda}(\xi_m)}, \end{align} $$
$$ \begin{align} \sigma_{\mu}(\vec{{\xi}}\,)=\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in (\mathbb Z^n)^m}{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots\Psi_{G_m,k_m}^{\lambda}(\xi_m)}, \end{align} $$
where
Let
![]() $M:=\Big [ \frac {(m-1)n}{2}\Big ]+1$
and choose
$M:=\Big [ \frac {(m-1)n}{2}\Big ]+1$
and choose
![]() $1<q<\frac {2m}{m-1}$
such that
$1<q<\frac {2m}{m-1}$
such that
 $$ \begin{align} \frac{(m-1)n}{2}<\frac{mn}{q}<\min{(a,M)}. \end{align} $$
$$ \begin{align} \frac{(m-1)n}{2}<\frac{mn}{q}<\min{(a,M)}. \end{align} $$
In view of (2.2), we have
 $$ \begin{align} \big\Vert \{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\}_{\vec{{k}}\,\in (\mathbb Z^n)^m}\big\Vert_{\ell^q} &\lesssim 2^{-\lambda (M-mn/q+mn/2)}\Vert \sigma_{\mu}\Vert_{L_M^q((\mathbb R^n)^m)}\nonumber\\ & \lesssim 2^{-\lambda (M-mn/q+mn/2)} 2^{-{\mu}(a-mn/q)}, \end{align} $$
$$ \begin{align} \big\Vert \{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\}_{\vec{{k}}\,\in (\mathbb Z^n)^m}\big\Vert_{\ell^q} &\lesssim 2^{-\lambda (M-mn/q+mn/2)}\Vert \sigma_{\mu}\Vert_{L_M^q((\mathbb R^n)^m)}\nonumber\\ & \lesssim 2^{-\lambda (M-mn/q+mn/2)} 2^{-{\mu}(a-mn/q)}, \end{align} $$
where the assumption (1.8) is applied in the last inequality.
We observe that if
![]() ${\mu }\ge {\mu }_0$
, then
${\mu }\ge {\mu }_0$
, then
![]() $b_{\vec {{G}},\vec {{k}}\,}^{\lambda ,\mu }$
vanishes unless
$b_{\vec {{G}},\vec {{k}}\,}^{\lambda ,\mu }$
vanishes unless
![]() $2^{\lambda +{\mu }-2}\le |\vec {{k}}\,|\le 2^{\lambda +{\mu }+2}$
due to the compact supports of
$2^{\lambda +{\mu }-2}\le |\vec {{k}}\,|\le 2^{\lambda +{\mu }+2}$
due to the compact supports of
![]() $\sigma _{\mu }$
and
$\sigma _{\mu }$
and
![]() $\Psi _{\vec {{G}},\vec {{k}}\,}^{\lambda }$
, which allows us to replace the sum over
$\Psi _{\vec {{G}},\vec {{k}}\,}^{\lambda }$
, which allows us to replace the sum over
![]() $\vec {{k}}\,\in (\mathbb Z^n)^m$
in (6.2) by the sum over
$\vec {{k}}\,\in (\mathbb Z^n)^m$
in (6.2) by the sum over
![]() $2^{\lambda +{\mu }-1}\le |\vec {{k}}\,|\le 2^{\lambda +{\mu }+1}$
. Moreover, we may consider only the case
$2^{\lambda +{\mu }-1}\le |\vec {{k}}\,|\le 2^{\lambda +{\mu }+1}$
. Moreover, we may consider only the case
![]() $|k_1|\ge \cdots \ge |k_m|$
as in the previous section. Therefore, in the rest of the section, we assume
$|k_1|\ge \cdots \ge |k_m|$
as in the previous section. Therefore, in the rest of the section, we assume
 $$ \begin{align*} \sigma_{\mu}(\vec{{\xi}}\,)&=\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in \mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in \mathcal{U}^{\lambda+{\mu}}}{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots\Psi_{G_m,k_m}^{\lambda}(\xi_m) }\\ &=\sum_{l=1}^{m}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in \mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in \mathcal{U}_l^{\lambda+{\mu}}}{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots\Psi_{G_m,k_m}^{\lambda}(\xi_m) }\\ &=:\sum_{l=1}^{m}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\sigma_{\mu,l}^{\lambda,\vec{{G}}}(\vec{{\xi}}\,), \end{align*} $$
$$ \begin{align*} \sigma_{\mu}(\vec{{\xi}}\,)&=\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in \mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in \mathcal{U}^{\lambda+{\mu}}}{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots\Psi_{G_m,k_m}^{\lambda}(\xi_m) }\\ &=\sum_{l=1}^{m}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in \mathcal{I}^{\lambda}}\sum_{\vec{{k}}\,\in \mathcal{U}_l^{\lambda+{\mu}}}{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\Psi_{G_1,k_1}^{\lambda}(\xi_1)\cdots\Psi_{G_m,k_m}^{\lambda}(\xi_m) }\\ &=:\sum_{l=1}^{m}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\sigma_{\mu,l}^{\lambda,\vec{{G}}}(\vec{{\xi}}\,), \end{align*} $$
where the sets
![]() $\mathcal {U}^{\lambda +\mu }$
and
$\mathcal {U}^{\lambda +\mu }$
and
![]() $\mathcal {U}_l^{\lambda +\mu }$
are defined as before. Then the left-hand side of (6.1) can be controlled by
$\mathcal {U}_l^{\lambda +\mu }$
are defined as before. Then the left-hand side of (6.1) can be controlled by
 $$ \begin{align} \bigg(\sum_{l=1}^{m}\sum_{{\mu}={\mu}_0}^{\infty}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\big\Vert \mathscr{M}_{\sigma_{{\mu},l}^{\lambda,\vec{{G}}}}(f_1,\dots,f_m)\big\Vert_{L^{2/m}}^{2/m} \bigg)^{m/2}. \end{align} $$
$$ \begin{align} \bigg(\sum_{l=1}^{m}\sum_{{\mu}={\mu}_0}^{\infty}\sum_{\lambda\in\mathbb{N}_0}\sum_{\vec{{G}}\in\mathcal{I}^{\lambda}}\big\Vert \mathscr{M}_{\sigma_{{\mu},l}^{\lambda,\vec{{G}}}}(f_1,\dots,f_m)\big\Vert_{L^{2/m}}^{2/m} \bigg)^{m/2}. \end{align} $$
Now we claim that
 $$ \begin{align} &\big\Vert \mathscr{M}_{\sigma_{{\mu},l}^{\lambda,\vec{{G}}}}(f_1,\dots,f_m)\big\Vert_{L^{2/m}}\nonumber\\ &\lesssim 2^{-\lambda (M-mn/q)}(\lambda+1)^{l/2}2^{-{\mu}(a-mn/q)}{\mu}^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align} $$
$$ \begin{align} &\big\Vert \mathscr{M}_{\sigma_{{\mu},l}^{\lambda,\vec{{G}}}}(f_1,\dots,f_m)\big\Vert_{L^{2/m}}\nonumber\\ &\lesssim 2^{-\lambda (M-mn/q)}(\lambda+1)^{l/2}2^{-{\mu}(a-mn/q)}{\mu}^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align} $$
Then (6.5) is less than a constant multiple of
![]() $\prod _{j=1}^{m}\Vert f_j\Vert _{L^2}$
as desired, due to the choice of q in (6.3).
$\prod _{j=1}^{m}\Vert f_j\Vert _{L^2}$
as desired, due to the choice of q in (6.3).
In order to prove (6.6), we use the estimates (2.7) and (2.8). We first rewrite
 $$ \begin{align*} \mathscr{M}_{\sigma_{{\mu},l}^{\lambda,\vec{{G}}}}\big(f_1,\dots,f_m\big)(x)=\sup_{\gamma\in\mathbb{Z}}\left| \sum_{\vec{{k}}\,\in \mathcal{U}_l^{\lambda+{\mu}}}{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \bigg( \prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_i(x)\bigg) }\right|, \end{align*} $$
$$ \begin{align*} \mathscr{M}_{\sigma_{{\mu},l}^{\lambda,\vec{{G}}}}\big(f_1,\dots,f_m\big)(x)=\sup_{\gamma\in\mathbb{Z}}\left| \sum_{\vec{{k}}\,\in \mathcal{U}_l^{\lambda+{\mu}}}{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \bigg( \prod_{j=1}^{m}L_{G_j,k_j}^{\lambda,\gamma}f_i(x)\bigg) }\right|, \end{align*} $$
where
![]() $L_{G,k}^{\lambda ,\gamma }$
is defined as in (2.3).
$L_{G,k}^{\lambda ,\gamma }$
is defined as in (2.3).
When
![]() $l=1$
, applying the embeddings
$l=1$
, applying the embeddings
![]() $\ell ^2\hookrightarrow \ell ^{\infty }$
,
$\ell ^2\hookrightarrow \ell ^{\infty }$
,
![]() $\ell ^q\hookrightarrow \ell ^{\infty }$
, and (2.7), the left-hand side of (6.6) is less than
$\ell ^q\hookrightarrow \ell ^{\infty }$
, and (2.7), the left-hand side of (6.6) is less than
 $$ \begin{align*} &\bigg\Vert \bigg(\sum_{\gamma\in\mathbb{Z}} \Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{1}^{\lambda+{\mu}}}{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \prod_{j=1}^{m}{L_{G_j,k_j}^{\lambda,\gamma}f_j} } \Big|^2 \bigg)^{1/2}\bigg\Vert_{L^{2/m}}\\ &\lesssim \big\Vert \{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \}_{\vec{{k}}\,\in (\mathbb Z^n)^m}\big\Vert_{\ell^{q}} \mu^{1/2}2^{\lambda mn/2}(\lambda+1)^{1/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}\\ &\lesssim 2^{-\lambda(M-mn/q)}(\lambda+1)^{1/2} 2^{-{\mu}(a-mn/q)} {\mu}^{1/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align*} $$
$$ \begin{align*} &\bigg\Vert \bigg(\sum_{\gamma\in\mathbb{Z}} \Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{1}^{\lambda+{\mu}}}{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \prod_{j=1}^{m}{L_{G_j,k_j}^{\lambda,\gamma}f_j} } \Big|^2 \bigg)^{1/2}\bigg\Vert_{L^{2/m}}\\ &\lesssim \big\Vert \{ b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \}_{\vec{{k}}\,\in (\mathbb Z^n)^m}\big\Vert_{\ell^{q}} \mu^{1/2}2^{\lambda mn/2}(\lambda+1)^{1/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}\\ &\lesssim 2^{-\lambda(M-mn/q)}(\lambda+1)^{1/2} 2^{-{\mu}(a-mn/q)} {\mu}^{1/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}, \end{align*} $$
where (6.4) is applied in the last inequality.
For the case
![]() $2\le l\le m$
, we can bound the left-hand side of (6.6) by
$2\le l\le m$
, we can bound the left-hand side of (6.6) by
 $$ \begin{align*} &\bigg\Vert \sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{l}^{\lambda+{\mu}}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \prod_{j=11}^{m} L_{G_j,k_j}^{\lambda,\gamma}f_j \Big| \bigg\Vert_{L^{2/m}}\\ &\lesssim \big\Vert \{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\}_{\vec{{k}}\,\in (\mathbb Z^n)^m}\big\Vert_{\ell^{q}} {\mu}^{l/2}2^{\lambda mn/2}(\lambda+1)^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align*} $$
$$ \begin{align*} &\bigg\Vert \sum_{\gamma\in\mathbb{Z}}\Big| \sum_{\vec{{k}}\,\in\mathcal{U}_{l}^{\lambda+{\mu}}} b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu} \prod_{j=11}^{m} L_{G_j,k_j}^{\lambda,\gamma}f_j \Big| \bigg\Vert_{L^{2/m}}\\ &\lesssim \big\Vert \{b_{\vec{{G}},\vec{{k}}\,}^{\lambda,\mu}\}_{\vec{{k}}\,\in (\mathbb Z^n)^m}\big\Vert_{\ell^{q}} {\mu}^{l/2}2^{\lambda mn/2}(\lambda+1)^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2}. \end{align*} $$
Here, we used the inequality (2.8) and the embedding
![]() $\ell ^q\hookrightarrow \ell ^{\infty }$
. Then the preceding expression is estimated by
$\ell ^q\hookrightarrow \ell ^{\infty }$
. Then the preceding expression is estimated by
 $$ \begin{align*} 2^{-\lambda (M-mn/q)}(\lambda+1)^{l/2}2^{-{\mu} (a-mn/q)}{\mu}^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} \end{align*} $$
$$ \begin{align*} 2^{-\lambda (M-mn/q)}(\lambda+1)^{l/2}2^{-{\mu} (a-mn/q)}{\mu}^{l/2}\prod_{j=1}^{m}\Vert f_j\Vert_{L^2} \end{align*} $$
7 Proof of Theorem 1.3
We now prove Theorem 1.3 taking Theorem 1.4 for granted.
First of all, it is easy to see that if
![]() $f_j$
are Schwartz functions on
$f_j$
are Schwartz functions on
![]() $\mathbb R^n$
, then
$\mathbb R^n$
, then
and
using the Lebesgue dominated convergence theorem and the property that
7.1 Extension of Theorem 1.4 to general
 $f_j\in L^2(\mathbb {R}^n)$
$f_j\in L^2(\mathbb {R}^n)$
Let
![]() $f_1,\dots ,f_m$
be given
$f_1,\dots ,f_m$
be given
![]() $L^2$
functions on
$L^2$
functions on
![]() $\mathbb {R}^n$
. As
$\mathbb {R}^n$
. As
![]() $S_{\sigma }^{\nu }(f_1 ,\dots , f_m ) $
is finite a.e. for each
$S_{\sigma }^{\nu }(f_1 ,\dots , f_m ) $
is finite a.e. for each
![]() $\nu \in \mathbb {Z}$
, there exists a set
$\nu \in \mathbb {Z}$
, there exists a set
![]() $E_{\nu }$
of measure zero so that
$E_{\nu }$
of measure zero so that
![]() $\big |S_{\sigma }^{\nu }(f_1 ,\dots , f_m ) \big |<\infty $
on the complement of
$\big |S_{\sigma }^{\nu }(f_1 ,\dots , f_m ) \big |<\infty $
on the complement of
![]() $E_{\nu }$
. Since
$E_{\nu }$
. Since
![]() $\nu $
ranges over a countable set
$\nu $
ranges over a countable set
![]() $\mathbb {Z}$
, the measure of
$\mathbb {Z}$
, the measure of
![]() $E:=\bigcup _{\nu \in \mathbb {Z}}E_{\nu }$
is clearly zero and thus we can define
$E:=\bigcup _{\nu \in \mathbb {Z}}E_{\nu }$
is clearly zero and thus we can define
on
![]() $E^c$
. That is,
$E^c$
. That is,
![]() $\mathscr {M}_{\sigma }(f_1,\dots , f_m)$
is well defined pointwise a.e. Moreover, it controls every
$\mathscr {M}_{\sigma }(f_1,\dots , f_m)$
is well defined pointwise a.e. Moreover, it controls every
![]() $\big | S_{\sigma }^{\nu }(f_1 ,\dots , f_m )\big |$
pointwise, whenever the latter is finite.
$\big | S_{\sigma }^{\nu }(f_1 ,\dots , f_m )\big |$
pointwise, whenever the latter is finite.
We now extend Theorem 1.5 to
![]() $f_j\in L^2(\mathbb R^n)$
using the above definition. Without loss of generality, we only consider the case when
$f_j\in L^2(\mathbb R^n)$
using the above definition. Without loss of generality, we only consider the case when
![]() $\nu \to -\infty $
as the case
$\nu \to -\infty $
as the case
![]() $\nu \to \infty $
follows similarly. As every sequence that converges in
$\nu \to \infty $
follows similarly. As every sequence that converges in
![]() $L^{2/m}$
has a subsequence that converges a.e., there are a set of measure zero
$L^{2/m}$
has a subsequence that converges a.e., there are a set of measure zero
![]() $E_{f_1,\dots , f_m}^1 $
and a subsequence
$E_{f_1,\dots , f_m}^1 $
and a subsequence
of the sequence of k’s such that
for all
![]() $x\in \mathbb R^n\setminus E_{f_1,\dots , f_m}^1$
. Next, there are a set of measure zero
$x\in \mathbb R^n\setminus E_{f_1,\dots , f_m}^1$
. Next, there are a set of measure zero
![]() $E_{f_1,\dots , f_m}^2$
and a subsequence
$E_{f_1,\dots , f_m}^2$
and a subsequence
of
such that
for all
![]() $x\in \mathbb R^n \setminus (E_{f_1,\dots , f_m}^2\cup E_{f_1,\dots , f_m}^2)$
. There are a set of measure zero
$x\in \mathbb R^n \setminus (E_{f_1,\dots , f_m}^2\cup E_{f_1,\dots , f_m}^2)$
. There are a set of measure zero
![]() $E_{f_1,\dots , f_m}^3$
and a subsequence
$E_{f_1,\dots , f_m}^3$
and a subsequence
of
such that
for all
![]() $x\in \mathbb R^n\setminus (E_{f_1,\dots , f_m}^1 \cup E_{f_1,\dots , f_m}^2 \cup E_{f_1,\dots , f_m}^3)$
. Iterating this process, we can take a diagonal sequence
$x\in \mathbb R^n\setminus (E_{f_1,\dots , f_m}^1 \cup E_{f_1,\dots , f_m}^2 \cup E_{f_1,\dots , f_m}^3)$
. Iterating this process, we can take a diagonal sequence
which is a subsequence of all subsequences, for which
![]() $f_j^{k_{\ell }^{\ell }}(x)\to f_j(x)$
for all
$f_j^{k_{\ell }^{\ell }}(x)\to f_j(x)$
for all
![]() $1\le j\le m$
and
$1\le j\le m$
and
as
![]() $\ell \to \infty $
for
$\ell \to \infty $
for
![]() $x\in \mathbb R^n\setminus \bigcup _{\rho =1}^{\infty } E_{f_1,\dots , f_m}^{\rho }$
and all
$x\in \mathbb R^n\setminus \bigcup _{\rho =1}^{\infty } E_{f_1,\dots , f_m}^{\rho }$
and all
![]() $\nu =-1,-2,\dots $
.
$\nu =-1,-2,\dots $
.
Now, on the set
![]() $ \mathbb R^n\setminus \bigcup _{\rho =1}^{\infty } E_{f_1,\dots , f_m}^{\rho }$
, we have
$ \mathbb R^n\setminus \bigcup _{\rho =1}^{\infty } E_{f_1,\dots , f_m}^{\rho }$
, we have
for every
![]() $\nu =-1,-2,\dots $
, and thus
$\nu =-1,-2,\dots $
, and thus
This deduces
on
![]() $ \mathbb R^n\setminus \bigcup _{\rho =1}^{\infty } E_{f_1,\dots , f_m}^{\rho }$
. Taking the
$ \mathbb R^n\setminus \bigcup _{\rho =1}^{\infty } E_{f_1,\dots , f_m}^{\rho }$
. Taking the
![]() $L^{2/m} $
quasi-norm on the both sides and using Fatou’s lemma and Theorem 1.4 for Schwartz functions, we finally obtain
$L^{2/m} $
quasi-norm on the both sides and using Fatou’s lemma and Theorem 1.4 for Schwartz functions, we finally obtain
 $$ \begin{align} \big\Vert \mathscr{M}_{\sigma}(f_1,\dots, f_m) \big\Vert_{L^{2/m}(\mathbb{R}^n)}\lesssim \prod_{j=1}^{m}\Vert f_j\Vert_{L^2(\mathbb R^n)} \end{align} $$
$$ \begin{align} \big\Vert \mathscr{M}_{\sigma}(f_1,\dots, f_m) \big\Vert_{L^{2/m}(\mathbb{R}^n)}\lesssim \prod_{j=1}^{m}\Vert f_j\Vert_{L^2(\mathbb R^n)} \end{align} $$
for
![]() $f_j\in L^2(\mathbb R^n)$
.
$f_j\in L^2(\mathbb R^n)$
.
7.2 Proof of Theorem 1.3
Let
![]() $f_j$
,
$f_j$
,
![]() $j=1,\dots ,m$
, be functions in
$j=1,\dots ,m$
, be functions in
![]() $L^2(\mathbb R^n)$
and
$L^2(\mathbb R^n)$
and
![]() $\{f_j^{k_{\ell }^{\ell }}\}_{\ell }$
be sequences that appeared above so that on
$\{f_j^{k_{\ell }^{\ell }}\}_{\ell }$
be sequences that appeared above so that on
![]() $(\bigcup _{\rho =1}^{\infty }E_{f_1,\dots ,f_m}^{\rho })^c$
,
$(\bigcup _{\rho =1}^{\infty }E_{f_1,\dots ,f_m}^{\rho })^c$
,
for each
![]() $\nu =-1,-2,\dots $
.
$\nu =-1,-2,\dots $
.
On
![]() $(\bigcup _{\rho =1}^{\infty }E_{f_1,\dots ,f_m}^{\rho })^c$
, we write
$(\bigcup _{\rho =1}^{\infty }E_{f_1,\dots ,f_m}^{\rho })^c$
, we write
 $$ \begin{align*} &\big| S_{\sigma}^{\nu}(f_1,\dots, f_m)(x) - \sigma(0)f_1(x)\cdots f_m(x) \big|\\ &\le \big| S_{\sigma}^{\nu}(f_1,\dots, f_m) - S_{\sigma}^{\nu}(f_1^{k_{\ell}^{\ell}},\dots, f_m^{k_{\ell}^{\ell}}) \big|\\ &\quad + \big| S_{\sigma}^{\nu}(f_1^{k_{\ell}^{\ell}},\dots, f_m^{k_{\ell}^{\ell}})- \sigma(0) f_1^{k_{\ell}^{\ell}} \cdots f_m^{k_{\ell}^{\ell}} \big|\\ &\quad \quad + \big| \sigma(0) f_1^{k_{\ell}^{\ell}} \cdots f_m^{k_{\ell}^{\ell}}-\sigma(0) f_1\cdots f_m \big|. \end{align*} $$
$$ \begin{align*} &\big| S_{\sigma}^{\nu}(f_1,\dots, f_m)(x) - \sigma(0)f_1(x)\cdots f_m(x) \big|\\ &\le \big| S_{\sigma}^{\nu}(f_1,\dots, f_m) - S_{\sigma}^{\nu}(f_1^{k_{\ell}^{\ell}},\dots, f_m^{k_{\ell}^{\ell}}) \big|\\ &\quad + \big| S_{\sigma}^{\nu}(f_1^{k_{\ell}^{\ell}},\dots, f_m^{k_{\ell}^{\ell}})- \sigma(0) f_1^{k_{\ell}^{\ell}} \cdots f_m^{k_{\ell}^{\ell}} \big|\\ &\quad \quad + \big| \sigma(0) f_1^{k_{\ell}^{\ell}} \cdots f_m^{k_{\ell}^{\ell}}-\sigma(0) f_1\cdots f_m \big|. \end{align*} $$
We first take
![]() $\limsup _{\nu \to -\infty }$
and use (7.1) to make the middle term on the right vanish, and then apply
$\limsup _{\nu \to -\infty }$
and use (7.1) to make the middle term on the right vanish, and then apply
![]() $\liminf _{\ell \to \infty }$
to handle the last term on the right which will vanish as well. As a result, we obtain
$\liminf _{\ell \to \infty }$
to handle the last term on the right which will vanish as well. As a result, we obtain
 $$ \begin{align*} &\limsup_{\nu \to -\infty}\big| S_{\sigma}^{\nu}(f_1,\dots, f_m) - \sigma(0) f_1\cdots f_m \big|\\ & \le \liminf_{\ell \to \infty} \sup_{\nu<0}\big| S_{\sigma}^{\nu}(f_1,\dots, f_m) - S_{\sigma}^{\nu}(f_1^{k_{\ell}^{\ell}},\dots, f_m^{k_{\ell}^{\ell}}) \big|. \end{align*} $$
$$ \begin{align*} &\limsup_{\nu \to -\infty}\big| S_{\sigma}^{\nu}(f_1,\dots, f_m) - \sigma(0) f_1\cdots f_m \big|\\ & \le \liminf_{\ell \to \infty} \sup_{\nu<0}\big| S_{\sigma}^{\nu}(f_1,\dots, f_m) - S_{\sigma}^{\nu}(f_1^{k_{\ell}^{\ell}},\dots, f_m^{k_{\ell}^{\ell}}) \big|. \end{align*} $$
Using the identity (5.2), we control the preceding expression pointwise by
 $$\begin{align*}\liminf_{\ell \to \infty} \sum_{i=1}^m \mathscr M_{\sigma} (f_1^{k_{\ell}^{\ell}},\dots, f_{i-1}^{k_{\ell}^{\ell}} ,f_i^{k_{\ell}^{\ell}} -f_i, f_{i+1},\dots, f_m ) \end{align*}$$
$$\begin{align*}\liminf_{\ell \to \infty} \sum_{i=1}^m \mathscr M_{\sigma} (f_1^{k_{\ell}^{\ell}},\dots, f_{i-1}^{k_{\ell}^{\ell}} ,f_i^{k_{\ell}^{\ell}} -f_i, f_{i+1},\dots, f_m ) \end{align*}$$
on the complement of the set
 $$\begin{align*}\bigcup_{\rho=1}^{\infty} \bigg[E_{f_1,\dots, f_m}^{\rho} \cup \bigg( \bigcup_{i=1}^m \bigcup_{\ell=1}^{\infty} E_{f_1^{k_{\ell}^{\ell}},\dots, f_{i-1}^{k_{\ell}^{\ell}} ,f_i^{k_{\ell}^{\ell}} -f_i, f_{i+1},\dots, f_m}^{\rho} \bigg)\bigg], \end{align*}$$
$$\begin{align*}\bigcup_{\rho=1}^{\infty} \bigg[E_{f_1,\dots, f_m}^{\rho} \cup \bigg( \bigcup_{i=1}^m \bigcup_{\ell=1}^{\infty} E_{f_1^{k_{\ell}^{\ell}},\dots, f_{i-1}^{k_{\ell}^{\ell}} ,f_i^{k_{\ell}^{\ell}} -f_i, f_{i+1},\dots, f_m}^{\rho} \bigg)\bigg], \end{align*}$$
which has full measure. Since
 $$\begin{align*}\Big\| \liminf_{\ell \to \infty}\sum_{i=1}^m \mathscr M_{\sigma} (f_1^{k_{\ell}^{\ell}},\dots, f_{i-1}^{k_{\ell}^{\ell}} ,f_i^{k_{\ell}^{\ell}} -f_i, f_{i+1},\dots, f_m ) \Big\|_{L^{2/m}(\mathbb R^n)} =0 \end{align*}$$
$$\begin{align*}\Big\| \liminf_{\ell \to \infty}\sum_{i=1}^m \mathscr M_{\sigma} (f_1^{k_{\ell}^{\ell}},\dots, f_{i-1}^{k_{\ell}^{\ell}} ,f_i^{k_{\ell}^{\ell}} -f_i, f_{i+1},\dots, f_m ) \Big\|_{L^{2/m}(\mathbb R^n)} =0 \end{align*}$$
in view of Fatou’s lemma and (7.2), we finally obtain
for almost all points in
![]() $ \mathbb R^n $
, which proves one part of the claimed a.e. convergences.
$ \mathbb R^n $
, which proves one part of the claimed a.e. convergences.
8 Concluding remarks
As of this writing, we are uncertain how to extend Theorem 1.4 in the nonlacunary case. A new ingredient may be necessary to accomplish this.
We have addressed the boundedness of several multilinear and maximal multilinear operators at the initial point
![]() $L^2\times \cdots \times L^2\to L^{2/m}$
. Our future investigation related to this project has two main directions: (a) to extend this initial estimate to many other operators, such as the general maximal multipliers considered in [Reference Grafakos, He and Honzík17, Reference Rubio de Francia26] and (b) to obtain
$L^2\times \cdots \times L^2\to L^{2/m}$
. Our future investigation related to this project has two main directions: (a) to extend this initial estimate to many other operators, such as the general maximal multipliers considered in [Reference Grafakos, He and Honzík17, Reference Rubio de Francia26] and (b) to obtain
![]() $L^{p_1}\times \cdots \times L^{p_m}\to L^{p}$
bounds for all of these operators in the largest possible range of exponents possible. Additionally, one could consider the study of related endpoint estimates. We hope to achieve this goal in future publications.
$L^{p_1}\times \cdots \times L^{p_m}\to L^{p}$
bounds for all of these operators in the largest possible range of exponents possible. Additionally, one could consider the study of related endpoint estimates. We hope to achieve this goal in future publications.