1 Introduction
Since the introduction of hyperbolic groups by Gromov in the 80s, a wealth of powerful tools have been developed to study them. Thus, when studying a class of groups, a classification of those that are hyperbolic can be very useful. We here focus on the class of one-relator groups, that is, groups of the form
![]() $F(\Sigma )/\langle \langle w \rangle \rangle $
, where
$F(\Sigma )/\langle \langle w \rangle \rangle $
, where
![]() $F(\Sigma )$
denotes the free group generated by
$F(\Sigma )$
denotes the free group generated by
![]() $\Sigma $
. The best possible statement that one could hope for is known as Gersten’s conjecture [Reference GerstenGer92b], which asserts that one-relator groups without Baumslag–Solitar subgroups are hyperbolic. In this article, we present some progress in this direction, building on our previous work in [Reference LintonLin22a, Reference LintonLin22b].
$\Sigma $
. The best possible statement that one could hope for is known as Gersten’s conjecture [Reference GerstenGer92b], which asserts that one-relator groups without Baumslag–Solitar subgroups are hyperbolic. In this article, we present some progress in this direction, building on our previous work in [Reference LintonLin22a, Reference LintonLin22b].
A Magnus subgroup of a one-relator group is a subgroup generated by a subset of the generators
![]() $\Sigma $
, omitting at least one generator mentioned in the cyclic reduction of w. The theory of one-relator groups originated in 1930, when Magnus proved the Freiheitssatz [Reference MagnusMag30].
$\Sigma $
, omitting at least one generator mentioned in the cyclic reduction of w. The theory of one-relator groups originated in 1930, when Magnus proved the Freiheitssatz [Reference MagnusMag30].
Theorem (Freiheitssatz)
Magnus subgroups of one-relator groups are free.
The proof of the Freiheitssatz makes use of a hierarchy of one-relator groups known as the Magnus hierarchy: a one-relator group G splits as an HNN-extension with one-relator vertex group H of lower “complexity” and where the edge groups are Magnus subgroups of H. By understanding the splittings that arise in this way, one may use induction to make conclusions about G. See [Reference LintonLin22a, Reference Lyndon and SchuppLS01, Reference Magnus, Karrass and SolitarMKS66] for various versions and applications of the Magnus hierarchy.
Almost a century later, the Magnus hierarchy is still a powerful tool for the study of one-relator groups. However, the splittings that arise remain somewhat mysterious. In [Reference LintonLin22a], the case that G is a
![]() $2$
-free one-relator group was considered in detail: there it was shown that if G is a finitely generated
$2$
-free one-relator group was considered in detail: there it was shown that if G is a finitely generated
![]() $2$
-free one-relator group, then G is hyperbolic and acts acylindrically on any Bass–Serre tree associated with a one-relator splitting. When G has torsion, the same properties hold [Reference LintonLin22a, Reference NewmanNew68, Reference WiseWis20]. On the other hand, the fact that Baumslag–Solitar groups cannot act acylindrically on a tree [Reference Minasyan and OsinMO15] implies that the general case is more complicated.
$2$
-free one-relator group, then G is hyperbolic and acts acylindrically on any Bass–Serre tree associated with a one-relator splitting. When G has torsion, the same properties hold [Reference LintonLin22a, Reference NewmanNew68, Reference WiseWis20]. On the other hand, the fact that Baumslag–Solitar groups cannot act acylindrically on a tree [Reference Minasyan and OsinMO15] implies that the general case is more complicated.
We say that a one-relator group
![]() $F(\Sigma )/\langle \langle w \rangle \rangle $
has an exceptional intersection if there are subsets
$F(\Sigma )/\langle \langle w \rangle \rangle $
has an exceptional intersection if there are subsets
![]() $A, B\subset \Sigma $
that generate Magnus subgroups and such that the following holds in the quotient:
$A, B\subset \Sigma $
that generate Magnus subgroups and such that the following holds in the quotient:
These groups were first studied by Collins in [Reference CollinsCol04]. Howie then obtained generalizations in the context of one-relator products of locally indicable groups in [Reference HowieHow05]. Examples of one-relator groups with exceptional intersections include torus knot groups
![]() $\langle a, b\mid a^p = b^q\rangle $
and closed orientable surface groups of genus at least two
$\langle a, b\mid a^p = b^q\rangle $
and closed orientable surface groups of genus at least two
![]() $\langle a_1, b_1, ..., a_g, b_g \mid [a_1, b_1] = [a_2, b_2]...[a_g, b_g]\rangle $
.
$\langle a_1, b_1, ..., a_g, b_g \mid [a_1, b_1] = [a_2, b_2]...[a_g, b_g]\rangle $
.
In [Reference LintonLin22a], it is shown that if
![]() $G = H*_{\psi }$
is a one-relator splitting where G does not contain any Baumslag–Solitar subgroups, H is hyperbolic and the edge groups of the splitting are quasi-convex and do not have exceptional intersection, then G acts acylindrically on its Bass–Serre tree and so is hyperbolic by [Reference Bestvina and FeighnBF92]. In light of this (and Theorem 4.7), when attempting to understand the hyperbolicity of one-relator groups, the case of interest lies when H has an exceptional intersection. In this article, we take a step in this direction and characterize
$G = H*_{\psi }$
is a one-relator splitting where G does not contain any Baumslag–Solitar subgroups, H is hyperbolic and the edge groups of the splitting are quasi-convex and do not have exceptional intersection, then G acts acylindrically on its Bass–Serre tree and so is hyperbolic by [Reference Bestvina and FeighnBF92]. In light of this (and Theorem 4.7), when attempting to understand the hyperbolicity of one-relator groups, the case of interest lies when H has an exceptional intersection. In this article, we take a step in this direction and characterize
![]() $2$
-free one-relator groups with exceptional intersection.
$2$
-free one-relator groups with exceptional intersection.
Theorem 3.17 Let G be a one-relator group with exceptional intersection. One of the following holds:
-
(1) G is
 $2$
-free.
$2$
-free. -
(2) There is a two-generator one-relator generalised Baumslag–Solitar subgroup
 $H<G$
such that every nonfree two-generator subgroup of G is conjugate into H.
$H<G$
such that every nonfree two-generator subgroup of G is conjugate into H.
It turns out that
![]() $2$
-free one-relator groups with an exceptional intersection have presentations of a particular form that can easily be described in terms of Christoffel words. We call these primitive exceptional intersection groups (see Section 3.1 for their description). The two-generator generalized Baumslag–Solitar subgroup appearing in the statement is a w-subgroup in the sense of [Reference Louder and WiltonLW22].
$2$
-free one-relator groups with an exceptional intersection have presentations of a particular form that can easily be described in terms of Christoffel words. We call these primitive exceptional intersection groups (see Section 3.1 for their description). The two-generator generalized Baumslag–Solitar subgroup appearing in the statement is a w-subgroup in the sense of [Reference Louder and WiltonLW22].
Thanks to the dichotomy provided by Theorem 3.17, with a little work we are able to establish quasi-convexity of Magnus subgroups of all hyperbolic one-relator groups.
Theorem 4.7 Magnus subgroups of hyperbolic one-relator groups are quasi-convex.
As a consequence, we prove Theorem 4.8, a strengthening of the main tool from [Reference LintonLin22a]. Note that hyperbolic one-relator groups can have distorted free subgroups as there are many hyperbolic (finitely generated free)-by-cyclic one-relator groups. See [Reference KapovichKap99] for an explicit example. Theorem 4.7 was already known in the case of one-relator groups with torsion by Newman’s Spelling Theorem [Reference NewmanNew68]. It was also known in the case of hyperbolic one-relator groups with quasi-convex one-relator hierarchies [Reference LintonLin22a].
Before stating our main result, we introduce two new families of two-generator one-relator groups. Let
![]() $p/q\in \mathbb {Q}_{>0}$
and denote by
$p/q\in \mathbb {Q}_{>0}$
and denote by
The first family is the fundamental group of the following graph of groups:

where
![]() $\{\langle x\rangle , \langle y\rangle \}$
form a malnormal family in
$\{\langle x\rangle , \langle y\rangle \}$
form a malnormal family in
![]() $F(A_{0, k})$
and
$F(A_{0, k})$
and
![]() $x, y\notin F(A_{1, k-1})$
. The upper edge homomorphism simply shifts the generators along. The second family is the fundamental group of the following graph of groups:
$x, y\notin F(A_{1, k-1})$
. The upper edge homomorphism simply shifts the generators along. The second family is the fundamental group of the following graph of groups:
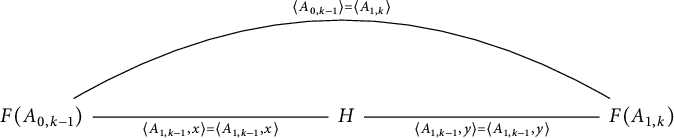
where H takes the following form
and where
![]() $\langle z\rangle $
is malnormal in
$\langle z\rangle $
is malnormal in
![]() $F(A_{1, k-1})$
and
$F(A_{1, k-1})$
and
![]() $x, y\notin F(A_{1, k-1})$
. We call these groups primitive extension groups. See Definition 5.1 for their formal definition.
$x, y\notin F(A_{1, k-1})$
. We call these groups primitive extension groups. See Definition 5.1 for their formal definition.
In Section 5, it is shown that primitive extension groups are two-generator one-relator groups. Examples of primitive extension groups include all one-relator ascending HNN-extensions of finitely generated free groups and, in particular,
![]() $\operatorname {\mathrm {BS}}(1, n)$
. These correspond to the families where
$\operatorname {\mathrm {BS}}(1, n)$
. These correspond to the families where
![]() $x = a_0$
and
$x = a_0$
and
![]() $p = 1$
(see Example 5.5). By [Reference MutanguhaMut21], the hyperbolicity of one-relator groups in these subfamilies are understood. Although two-generator one-relator hyperbolic groups have received some attention [Reference Gardam, Kielak and LoganGKL21, Reference Kapovich and WeidmannKW99], there are currently no further criteria that do not rely on small cancellation-like criteria to determine when a primitive extension group is hyperbolic.
$p = 1$
(see Example 5.5). By [Reference MutanguhaMut21], the hyperbolicity of one-relator groups in these subfamilies are understood. Although two-generator one-relator hyperbolic groups have received some attention [Reference Gardam, Kielak and LoganGKL21, Reference Kapovich and WeidmannKW99], there are currently no further criteria that do not rely on small cancellation-like criteria to determine when a primitive extension group is hyperbolic.
Our main result can now be stated as follows.
Theorem 5.6 A one-relator group is hyperbolic (and virtually special) if its primitive extension subgroups are hyperbolic (and virtually special).
It is immediate that Gersten’s conjecture [Reference GerstenGer92b] needs only to be proved for primitive extension groups in order to hold for all one-relator groups.
Corollary 5.7 Gersten’s conjecture is true if it is true for primitive extension groups.
Outline of the article
We begin the article with some preliminary results on free groups which we shall need for the proof of Theorem 3.17. In Section 3.1, we define primitive exceptional intersection groups and prove that they are all 2-free. In brief, the proof involves showing that any 2-generated subgroup of the underlying free group containing the relator must contain it as a primitive element. We may then appeal to a result of Louder–Wilton [Reference Louder and WiltonLW22]. This is the most involved part of the article as the proof is rather technical and splits into several cases. Then Section 3.2 is dedicated to finding Baumslag–Solitar subgroups in all other one-relator groups with exceptional intersection and thus establishing Theorem 3.17. In Section 4, we refine the tools established in [Reference LintonLin22a]. We first show that one-relator complexes admit stable hierarchies that terminate at a primitive extension complex. This is the key result from where the importance of primitive extension groups for understanding the structure of one-relator groups can be derived. The main point in the proof is that if G is a one-relator group that is not a primitive extension group, then we can always find an HNN-splitting of G over another one-relator group without exceptional intersections. As such, primitive extension subgroups arise essentially as the obstructions to acylindrical hierarchies. Using this “relative” hierarchy, we may then appeal to the combination theorems proved in [Reference LintonLin22a] in order to establish Theorems 4.7 and 4.8. Finally, in Section 5, we define primitive extension groups, show that primitive extension complexes have primitive extension fundamental groups, and combine our results to prove Theorem 5.6.
2 Preliminaries on free groups
In this section, we recall some standard material from the theory of free groups and prove some technical results that will be of use to us for the proof of Theorem 3.17.
If
![]() $\Sigma $
is a set, we denote by
$\Sigma $
is a set, we denote by
![]() $F(\Sigma )$
the free group, freely generated by
$F(\Sigma )$
the free group, freely generated by
![]() $\Sigma $
. If
$\Sigma $
. If
![]() $\Delta $
is another set, we write
$\Delta $
is another set, we write
![]() $F(\Sigma , \Delta ) = F(\Sigma \sqcup \Delta )$
.
$F(\Sigma , \Delta ) = F(\Sigma \sqcup \Delta )$
.
2.1 Proper powers
We say an element
![]() $w\in F(\Sigma )$
is a proper power if there is some
$w\in F(\Sigma )$
is a proper power if there is some
![]() $u\in F(\Sigma )$
and
$u\in F(\Sigma )$
and
![]() $n\geq 2$
such that
$n\geq 2$
such that
![]() $w = u^n$
.
$w = u^n$
.
Lemma 2.1 Let
![]() $1 \neq y^{-1}zy\in F(\Sigma )$
be freely reduced with z cyclically reduced and not equal to a proper power. Then:
$1 \neq y^{-1}zy\in F(\Sigma )$
be freely reduced with z cyclically reduced and not equal to a proper power. Then:
-
(1) If
 $y = 1$
and there is some
$y = 1$
and there is some
 $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
 $g, h\in F(\Sigma )$
such that
$g, h\in F(\Sigma )$
such that
 $z^i = gzh$
is freely reduced, then
$z^i = gzh$
is freely reduced, then
 $i\geq 1$
and
$i\geq 1$
and
 $g,h\in \langle z\rangle $
.
$g,h\in \langle z\rangle $
. -
(2) If
 $y\neq 1$
and there is some
$y\neq 1$
and there is some
 $i, j\in \mathbb {Z}$
,
$i, j\in \mathbb {Z}$
,
 $g, h\in F(\Sigma )$
such that
$g, h\in F(\Sigma )$
such that
 $y^{-1}z^iy = gy^{-1}z^jyh$
is freely reduced, then
$y^{-1}z^iy = gy^{-1}z^jyh$
is freely reduced, then
 $g, h = 1$
and
$g, h = 1$
and
 $i = j$
.
$i = j$
.
Proof Suppose for a contradiction that the first assertion does not hold. We may assume that
![]() $i = 2$
or
$i = 2$
or
![]() $i = -2$
. Then
$i = -2$
. Then
![]() $z = z'z" = z"z'$
in the first case and
$z = z'z" = z"z'$
in the first case and
![]() $z = z'z" = (z')^{-1}(z")^{-1}$
in the second. But then the first case cannot happen by [Reference Lyndon and SchützenbergerLS62, Lemma 3] and the second case cannot happen as a nontrivial element of a free group cannot be conjugate to its own inverse. Thus, the first assertion holds.
$z = z'z" = (z')^{-1}(z")^{-1}$
in the second. But then the first case cannot happen by [Reference Lyndon and SchützenbergerLS62, Lemma 3] and the second case cannot happen as a nontrivial element of a free group cannot be conjugate to its own inverse. Thus, the first assertion holds.
For the proof of the second assertion, we use the first assertion and the fact that z is cyclically reduced.
Lemma 2.2 Let
![]() $F(\Sigma )$
be a free group with
$F(\Sigma )$
be a free group with
![]() $\Sigma = A\sqcup B$
, and let
$\Sigma = A\sqcup B$
, and let
![]() $b\in \langle B\rangle $
and
$b\in \langle B\rangle $
and
![]() $z\in F(\Sigma )$
be freely reduced elements. Suppose that z begins and ends with generators in
$z\in F(\Sigma )$
be freely reduced elements. Suppose that z begins and ends with generators in
![]() $A\sqcup A^{-1}$
, that
$A\sqcup A^{-1}$
, that
![]() $zb$
is not a proper power and that there are elements
$zb$
is not a proper power and that there are elements
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $g, h\in F(\Sigma )$
such that
$g, h\in F(\Sigma )$
such that
![]() $(zb)^i = gzh$
is freely reduced. Then
$(zb)^i = gzh$
is freely reduced. Then
![]() $i\geq 1$
and
$i\geq 1$
and
![]() $g\in \langle zb\rangle $
.
$g\in \langle zb\rangle $
.
Proof By Lemma 2.1, we may assume that
![]() $b\neq 1$
. If
$b\neq 1$
. If
![]() $i\leq -1$
, since b does not mention any
$i\leq -1$
, since b does not mention any
![]() $A\sqcup A^{-1}$
generators, it follows that z has a nontrivial prefix equal to its own inverse. Since this is not possible, we may also assume that
$A\sqcup A^{-1}$
generators, it follows that z has a nontrivial prefix equal to its own inverse. Since this is not possible, we may also assume that
![]() $i\geq 1$
.
$i\geq 1$
.
Now suppose for a contradiction that
![]() $i\geq 1$
and
$i\geq 1$
and
![]() $g\notin \langle zb\rangle $
. Then we have equalities of the form:
$g\notin \langle zb\rangle $
. Then we have equalities of the form:
for some
![]() $z_1, z_2, z_3\in F(\Sigma )$
, where the words on the right-hand side are freely reduced.
$z_1, z_2, z_3\in F(\Sigma )$
, where the words on the right-hand side are freely reduced.
We show by induction on
![]() ${\lvert {z_1} \rvert } + {\lvert {z_3} \rvert }$
that
${\lvert {z_1} \rvert } + {\lvert {z_3} \rvert }$
that
![]() $z_2 = b$
. If
$z_2 = b$
. If
![]() ${\lvert {z_1} \rvert } = {\lvert {z_3} \rvert }$
, then clearly
${\lvert {z_1} \rvert } = {\lvert {z_3} \rvert }$
, then clearly
![]() $z_2 = b$
. So suppose that
$z_2 = b$
. So suppose that
![]() ${\lvert {z_1} \rvert } < {\lvert {z_3} \rvert }$
, the other case is symmetric. Since the first letter of
${\lvert {z_1} \rvert } < {\lvert {z_3} \rvert }$
, the other case is symmetric. Since the first letter of
![]() $z_3$
is in
$z_3$
is in
![]() $A\sqcup A^{-1}$
and
$A\sqcup A^{-1}$
and
![]() $b\in \langle B\rangle $
, we have that
$b\in \langle B\rangle $
, we have that
![]() ${\lvert {z_3} \rvert }> {\lvert {z_1z_2} \rvert }$
. Now, by [Reference Lyndon and SchützenbergerLS62, Lemma 2], we have
${\lvert {z_3} \rvert }> {\lvert {z_1z_2} \rvert }$
. Now, by [Reference Lyndon and SchützenbergerLS62, Lemma 2], we have
![]() $z_3 = (z_1z_2)^iz'$
for some
$z_3 = (z_1z_2)^iz'$
for some
![]() $i\geq 1$
and where
$i\geq 1$
and where
![]() $z'$
is a proper prefix of
$z'$
is a proper prefix of
![]() $z_1z_2$
. Then we get
$z_1z_2$
. Then we get
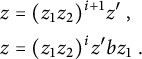 $$ \begin{align*} z &= (z_1z_2)^{i+1}z'~,\\ z &= (z_1z_2)^iz'bz_1~. \end{align*} $$
$$ \begin{align*} z &= (z_1z_2)^{i+1}z'~,\\ z &= (z_1z_2)^iz'bz_1~. \end{align*} $$
By comparing suffixes, we have
But now we obtain equalities of the same form as before, with
![]() $z'$
playing the role of
$z'$
playing the role of
![]() $z_3$
. Since
$z_3$
. Since
![]() ${\lvert {z'} \rvert } < {\lvert {z_3} \rvert }$
, by induction, we see that
${\lvert {z'} \rvert } < {\lvert {z_3} \rvert }$
, by induction, we see that
![]() $z_2 = b$
.
$z_2 = b$
.
If
![]() $z_2 = b$
, then
$z_2 = b$
, then
![]() $zb$
is a conjugate of itself and so must be a proper power by [Reference Lyndon and SchützenbergerLS62, Lemma 3]. Thus, we obtain the required contradiction and conclude that
$zb$
is a conjugate of itself and so must be a proper power by [Reference Lyndon and SchützenbergerLS62, Lemma 3]. Thus, we obtain the required contradiction and conclude that
![]() $g \in \langle zb\rangle $
.
$g \in \langle zb\rangle $
.
2.2 Subgroups
A graph is a one-dimensional CW-complex. A morphism of graphs
![]() $\Gamma \to \Delta $
is a map sending vertices to vertices and edges homeomorphically to edges. A morphism of graphs is an immersion, denoted by
$\Gamma \to \Delta $
is a map sending vertices to vertices and edges homeomorphically to edges. A morphism of graphs is an immersion, denoted by
![]() $\looparrowright $
, if it is locally injective. It is a fundamental observation due to Stallings [Reference StallingsSta83] that subgroups of free groups can be represented by immersions of pointed graphs
$\looparrowright $
, if it is locally injective. It is a fundamental observation due to Stallings [Reference StallingsSta83] that subgroups of free groups can be represented by immersions of pointed graphs
![]() $(\Gamma , x)\looparrowright (\Delta , y)$
. The core of a graph
$(\Gamma , x)\looparrowright (\Delta , y)$
. The core of a graph
![]() $\Gamma $
, denoted by
$\Gamma $
, denoted by
![]() $\operatorname {\mathrm {Core}}(\Gamma )$
, is the union of the images of all immersed cycles
$\operatorname {\mathrm {Core}}(\Gamma )$
, is the union of the images of all immersed cycles
![]() $S^1\looparrowright \Gamma $
. Then conjugacy classes of subgroups of free groups can be represented by immersions of core graphs
$S^1\looparrowright \Gamma $
. Then conjugacy classes of subgroups of free groups can be represented by immersions of core graphs
![]() $\Gamma \looparrowright \Delta $
.
$\Gamma \looparrowright \Delta $
.
Lemma 2.3 Let
![]() $F(A, B, C)$
be a free group, and let
$F(A, B, C)$
be a free group, and let
![]() $x\in \langle A, B\rangle - \langle B\rangle $
and
$x\in \langle A, B\rangle - \langle B\rangle $
and
![]() $y\in \langle B, C\rangle - \langle B\rangle $
. If
$y\in \langle B, C\rangle - \langle B\rangle $
. If
![]() $H<F(A, B, C)$
is a subgroup of rank two, containing
$H<F(A, B, C)$
is a subgroup of rank two, containing
![]() $\langle x, y\rangle $
, then one of the following holds:
$\langle x, y\rangle $
, then one of the following holds:
-
(1) There are elements
 $u, v$
and nonzero integers
$u, v$
and nonzero integers
 $i, j$
, such that
$i, j$
, such that
 $H = \langle u, v\rangle $
and
$H = \langle u, v\rangle $
and
 $x = u^i$
,
$x = u^i$
,
 $y = v^j$
.
$y = v^j$
. -
(2) There are elements
 $u, v, w$
and nonzero integers
$u, v, w$
and nonzero integers
 $i, j$
such that
$i, j$
such that
 $H = \langle u^{-1}wu, u^{-1}v\rangle $
and
$H = \langle u^{-1}wu, u^{-1}v\rangle $
and
 $x = u^{-1}w^iu$
,
$x = u^{-1}w^iu$
,
 $y = v^{-1}w^jv$
.
$y = v^{-1}w^jv$
.
Proof Let
![]() $\Delta $
be a rose graph with one edge for each element in
$\Delta $
be a rose graph with one edge for each element in
![]() $A\sqcup B\sqcup C$
so that we may identify
$A\sqcup B\sqcup C$
so that we may identify
![]() $\pi _1(\Delta )$
with
$\pi _1(\Delta )$
with
![]() $F(A, B, C)$
. Then we may represent
$F(A, B, C)$
. Then we may represent
![]() $\langle x, y\rangle $
and H by graph immersions
$\langle x, y\rangle $
and H by graph immersions
![]() $\Gamma \looparrowright \Delta $
and
$\Gamma \looparrowright \Delta $
and
![]() $\Lambda \looparrowright \Delta $
. By assumption,
$\Lambda \looparrowright \Delta $
. By assumption,
![]() $\Gamma \looparrowright \Delta $
factors through
$\Gamma \looparrowright \Delta $
factors through
![]() $\Lambda \looparrowright \Delta $
. Thus, there must be loops based at the same vertex in
$\Lambda \looparrowright \Delta $
. Thus, there must be loops based at the same vertex in
![]() $\Lambda $
with labels x and y, covering
$\Lambda $
with labels x and y, covering
![]() $\Lambda $
. Since a path labeled by x cannot traverse any C-edges and a path labeled by y cannot traverse any A-edges, it follows that there is a decomposition
$\Lambda $
. Since a path labeled by x cannot traverse any C-edges and a path labeled by y cannot traverse any A-edges, it follows that there is a decomposition
![]() $Q^{(1)} = Q_1\cup Q_2$
where
$Q^{(1)} = Q_1\cup Q_2$
where
![]() $\chi (Q_1), \chi (Q_2) = 0$
and
$\chi (Q_1), \chi (Q_2) = 0$
and
![]() $Q_1$
only contains A-edges and B-edges and
$Q_1$
only contains A-edges and B-edges and
![]() $Q_2$
only contains B-edges and C-edges. Moreover, the path labeled by x is supported in
$Q_2$
only contains B-edges and C-edges. Moreover, the path labeled by x is supported in
![]() $Q_1$
and the path labeled by y is supported in
$Q_1$
and the path labeled by y is supported in
![]() $Q_2$
. If
$Q_2$
. If
![]() $Q_1\cap Q_2$
is connected, (1) must hold. If
$Q_1\cap Q_2$
is connected, (1) must hold. If
![]() $Q_1\cap Q_2$
is not connected, then (2) must hold.
$Q_1\cap Q_2$
is not connected, then (2) must hold.
Lemma 2.4 Let
![]() $F(A, B, C)$
be a free group, and let
$F(A, B, C)$
be a free group, and let
![]() $x\in \langle A, B\rangle - \langle B\rangle $
,
$x\in \langle A, B\rangle - \langle B\rangle $
,
![]() $y\in \langle B, C\rangle - \langle B\rangle $
, and
$y\in \langle B, C\rangle - \langle B\rangle $
, and
![]() $z\in \langle B\rangle - 1$
. If
$z\in \langle B\rangle - 1$
. If
![]() $H<F(A, B, C)$
is a subgroup of rank two, containing
$H<F(A, B, C)$
is a subgroup of rank two, containing
![]() $\langle xy, z\rangle $
, then there is an element u and a nonzero integer i, such that
$\langle xy, z\rangle $
, then there is an element u and a nonzero integer i, such that
![]() $H = \langle xy, u\rangle $
and
$H = \langle xy, u\rangle $
and
![]() $z = u^i$
.
$z = u^i$
.
Proof Just as in the proof of Lemma 2.3, let
![]() $\Delta $
be a rose graph with one edge for each element in
$\Delta $
be a rose graph with one edge for each element in
![]() $A\sqcup B\sqcup C$
so that we may identify
$A\sqcup B\sqcup C$
so that we may identify
![]() $\pi _1(\Delta )$
with
$\pi _1(\Delta )$
with
![]() $F(A, B, C)$
. Then we may represent
$F(A, B, C)$
. Then we may represent
![]() $\langle xy, z\rangle $
and H by graph immersions
$\langle xy, z\rangle $
and H by graph immersions
![]() $\Gamma \looparrowright \Delta $
and
$\Gamma \looparrowright \Delta $
and
![]() $\Lambda \looparrowright \Delta $
. By assumption,
$\Lambda \looparrowright \Delta $
. By assumption,
![]() $\Gamma \looparrowright \Delta $
factors through
$\Gamma \looparrowright \Delta $
factors through
![]() $\Lambda \looparrowright \Delta $
. Thus, there must be loops based at the same vertex in
$\Lambda \looparrowright \Delta $
. Thus, there must be loops based at the same vertex in
![]() $\Lambda $
with labels
$\Lambda $
with labels
![]() $xy$
and z, covering
$xy$
and z, covering
![]() $\Lambda $
. Since z only traverses B-edges, it follows that there is a decomposition
$\Lambda $
. Since z only traverses B-edges, it follows that there is a decomposition
![]() $Q^{(1)} = Q_1\cup Q_2\cup Q_3$
where
$Q^{(1)} = Q_1\cup Q_2\cup Q_3$
where
![]() $\chi (Q_1) = 0$
,
$\chi (Q_1) = 0$
,
![]() $Q_1$
only contains B-edges,
$Q_1$
only contains B-edges,
![]() $\chi (Q_2) = \chi (Q_3) = 1$
,
$\chi (Q_2) = \chi (Q_3) = 1$
,
![]() $Q_2$
only contains A-edges and B-edges, and
$Q_2$
only contains A-edges and B-edges, and
![]() $Q_3$
only contains B-edges and C-edges. Moreover, z is supported in
$Q_3$
only contains B-edges and C-edges. Moreover, z is supported in
![]() $Q_1$
, x is supported in
$Q_1$
, x is supported in
![]() $Q_1\cup Q_2$
, and y is supported in
$Q_1\cup Q_2$
, and y is supported in
![]() $Q_1\cup Q_3$
. Now the result follows.
$Q_1\cup Q_3$
. Now the result follows.
The fiber product
![]() $\Gamma \times _{\Delta }\Lambda $
of two graph immersions
$\Gamma \times _{\Delta }\Lambda $
of two graph immersions
![]() $f:\Gamma \looparrowright \Delta $
,
$f:\Gamma \looparrowright \Delta $
,
![]() $g:\Lambda \looparrowright \Delta $
is defined as the graph with vertices
$g:\Lambda \looparrowright \Delta $
is defined as the graph with vertices
and edges
As elucidated in [Reference StallingsSta83], there is a correspondence between the double cosets
![]() $\pi _1(\Lambda )h\pi _1(\Gamma )$
such that
$\pi _1(\Lambda )h\pi _1(\Gamma )$
such that
![]() $\pi _1(\Gamma )\cap \pi _1(\Lambda )^h \neq 1$
and components of the core of the fiber product graph
$\pi _1(\Gamma )\cap \pi _1(\Lambda )^h \neq 1$
and components of the core of the fiber product graph
![]() $\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
given by the
$\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
given by the
![]() $\pi _1$
functor.
$\pi _1$
functor.
3 Exceptional intersection groups
The interactions between Magnus subgroups of one-relator groups are well understood. The following is [Reference CollinsCol04, Theorem 2].
Theorem 3.1 Let
![]() $F(\Sigma )/\langle \langle w \rangle \rangle $
be a one-relator group and suppose
$F(\Sigma )/\langle \langle w \rangle \rangle $
be a one-relator group and suppose
![]() $\Sigma = A\sqcup B\sqcup C$
. If
$\Sigma = A\sqcup B\sqcup C$
. If
![]() $\langle A, B\rangle $
and
$\langle A, B\rangle $
and
![]() $\langle B, C\rangle $
are Magnus subgroups, then one of the following holds:
$\langle B, C\rangle $
are Magnus subgroups, then one of the following holds:
-
(1)
 $\langle A, B\rangle \cap \langle B, C\rangle = \langle B\rangle $
.
$\langle A, B\rangle \cap \langle B, C\rangle = \langle B\rangle $
. -
(2)
 $\langle A, B\rangle \cap \langle B, C\rangle = \langle B\rangle *\mathbb {Z}$
.
$\langle A, B\rangle \cap \langle B, C\rangle = \langle B\rangle *\mathbb {Z}$
.
We say that the Magnus subgroups
![]() $\langle A, B\rangle $
and
$\langle A, B\rangle $
and
![]() $\langle B, C\rangle $
have exceptional intersection if the latter situation occurs.
$\langle B, C\rangle $
have exceptional intersection if the latter situation occurs.
Definition 3.1 A one-relator presentation
![]() $\langle \Sigma \mid w\rangle $
is an exceptional intersection presentation if there are disjoint subsets
$\langle \Sigma \mid w\rangle $
is an exceptional intersection presentation if there are disjoint subsets
![]() $A, B, C\subset \Sigma $
such that
$A, B, C\subset \Sigma $
such that
![]() $\langle A, B\rangle $
and
$\langle A, B\rangle $
and
![]() $\langle B, C\rangle $
have exceptional intersection. A one-relator group G is an exceptional intersection group if it has an exceptional intersection presentation.
$\langle B, C\rangle $
have exceptional intersection. A one-relator group G is an exceptional intersection group if it has an exceptional intersection presentation.
The following result appears as [Reference CollinsCol04, Corollary 2.3].
Corollary 3.2 Exceptional intersection groups are torsion-free.
3.1 Primitive exceptional intersection groups
In this section, we introduce two families of one-relator groups called primitive exceptional intersection groups. Our aim will be to show that they are precisely the exceptional intersection groups that are
![]() $2$
-free.
$2$
-free.
Before defining our groups, we first need to discuss certain primitive elements of the free group of rank two. Recall that an element of a free group
![]() $w\in F(\Sigma )$
is primitive if w forms part of a free basis for
$w\in F(\Sigma )$
is primitive if w forms part of a free basis for
![]() $F(\Sigma )$
. Otherwise, w is imprimitive. The primitive elements of interest to us are known as Christoffel words and were first introduced in [Reference ChristoffelChr73]. They are parametrized by a rational slope
$F(\Sigma )$
. Otherwise, w is imprimitive. The primitive elements of interest to us are known as Christoffel words and were first introduced in [Reference ChristoffelChr73]. They are parametrized by a rational slope
![]() $p/q\in \mathbb {Q}_{>0}$
. Let
$p/q\in \mathbb {Q}_{>0}$
. Let
![]() $\Gamma \subset \mathbb {R}^2$
denote the Cayley graph for
$\Gamma \subset \mathbb {R}^2$
denote the Cayley graph for
![]() $\mathbb {Z}^2$
on the generating set
$\mathbb {Z}^2$
on the generating set
![]() $a = (1, 0)$
,
$a = (1, 0)$
,
![]() $b = (0, 1)$
. Let
$b = (0, 1)$
. Let
![]() $L\subset \mathbb {R}^2$
be the line segment beginning at the origin and ending at the vertex
$L\subset \mathbb {R}^2$
be the line segment beginning at the origin and ending at the vertex
![]() $(q, p)$
. Now let
$(q, p)$
. Now let
![]() $P\subset \Gamma $
be the shortest length edge path connecting the endpoints of L, remaining below L and such that there are no integral points contained in the region enclosed by
$P\subset \Gamma $
be the shortest length edge path connecting the endpoints of L, remaining below L and such that there are no integral points contained in the region enclosed by
![]() $L\cup P$
. See Figure 1 for an example. The word in a and b traced out by P is denoted by
$L\cup P$
. See Figure 1 for an example. The word in a and b traced out by P is denoted by
By [Reference Osborne and ZieschangOZ81, Theorem 1.2], every primitive element of
![]() $F(a, b)$
is conjugate into the set
$F(a, b)$
is conjugate into the set
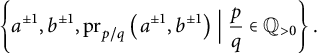 $$\begin{align*}\left\{a^{\pm1}, b^{\pm1}, \operatorname{\mathrm{pr}}_{p/q}\left(a^{\pm1}, b^{\pm1}\right) \Bigm\vert \frac{p}{q}\in \mathbb{Q}_{> 0}\right\}. \end{align*}$$
$$\begin{align*}\left\{a^{\pm1}, b^{\pm1}, \operatorname{\mathrm{pr}}_{p/q}\left(a^{\pm1}, b^{\pm1}\right) \Bigm\vert \frac{p}{q}\in \mathbb{Q}_{> 0}\right\}. \end{align*}$$

Figure 1:
L is in green with slope
![]() $5/6$
. The a edges are in blue and the b edges are in red, so
$5/6$
. The a edges are in blue and the b edges are in red, so
![]() $\operatorname {\mathrm {pr}}_{5/6}(a, b) = a^2babababab$
.
$\operatorname {\mathrm {pr}}_{5/6}(a, b) = a^2babababab$
.
Now consider the free group
![]() $F(A, B, C)$
, freely generated by disjoint sets
$F(A, B, C)$
, freely generated by disjoint sets
![]() $A, B, C$
. Let
$A, B, C$
. Let
![]() $p/q\in \mathbb {Q}_{>0}$
and let
$p/q\in \mathbb {Q}_{>0}$
and let
 $$ \begin{align*} x &\in \langle A, B\rangle - \langle B\rangle~,\\ y &\in \langle B, C\rangle - \langle B\rangle~. \end{align*} $$
$$ \begin{align*} x &\in \langle A, B\rangle - \langle B\rangle~,\\ y &\in \langle B, C\rangle - \langle B\rangle~. \end{align*} $$
Then we call
![]() $\operatorname {\mathrm {pr}}_{p/q}(x, y)$
a primitive exceptional intersection word of the first type if the following hold:
$\operatorname {\mathrm {pr}}_{p/q}(x, y)$
a primitive exceptional intersection word of the first type if the following hold:
-
(1)
 $\{\langle x\rangle , \langle y\rangle \}$
is a malnormal family (that is,
$\{\langle x\rangle , \langle y\rangle \}$
is a malnormal family (that is,
 $\langle x\rangle $
and
$\langle x\rangle $
and
 $\langle y\rangle $
are malnormal and no conjugate of
$\langle y\rangle $
are malnormal and no conjugate of
 $\langle x\rangle $
intersects
$\langle x\rangle $
intersects
 $\langle y\rangle $
nontrivially).
$\langle y\rangle $
nontrivially). -
(2) If
 $p/q = 1$
, then there is no
$p/q = 1$
, then there is no
 $a\in \langle A, B\rangle - \langle B\rangle $
,
$a\in \langle A, B\rangle - \langle B\rangle $
,
 $c\in \langle B, C\rangle - \langle B\rangle $
such that
$c\in \langle B, C\rangle - \langle B\rangle $
such that
 $\operatorname {\mathrm {pr}}_{1}(x, y) = \operatorname {\mathrm {pr}}_{1}(a, c)$
and
$\operatorname {\mathrm {pr}}_{1}(x, y) = \operatorname {\mathrm {pr}}_{1}(a, c)$
and
 $\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family.
$\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family.
By definition, we see that
![]() $\langle x, y\rangle $
is an infinite cyclic subgroup of
$\langle x, y\rangle $
is an infinite cyclic subgroup of
![]() $G = F(A, B, C)/\langle \langle w \rangle \rangle $
. We find that G has the following exceptional intersection:
$G = F(A, B, C)/\langle \langle w \rangle \rangle $
. We find that G has the following exceptional intersection:
The following example demonstrates why we require the second condition in the definition.
Example 3.3 Consider the word
![]() $\operatorname {\mathrm {pr}}_{1}(a^2b^{-1}, bc^2)\in F(a, b, c)$
. Although the subgroups
$\operatorname {\mathrm {pr}}_{1}(a^2b^{-1}, bc^2)\in F(a, b, c)$
. Although the subgroups
![]() $\{\langle a^2b^{-1}\rangle , \langle bc^2\rangle \}$
form a malnormal family, we have
$\{\langle a^2b^{-1}\rangle , \langle bc^2\rangle \}$
form a malnormal family, we have
where
![]() $\{\langle a^2\rangle , \langle c^2\rangle \}$
is not a malnormal family. Hence,
$\{\langle a^2\rangle , \langle c^2\rangle \}$
is not a malnormal family. Hence,
![]() $\operatorname {\mathrm {pr}}_1(a^2b^{-1}, bc^2)$
is not a primitive exceptional intersection word of the first type.
$\operatorname {\mathrm {pr}}_1(a^2b^{-1}, bc^2)$
is not a primitive exceptional intersection word of the first type.
Now let
![]() $z\in \langle B\rangle - 1$
. We call
$z\in \langle B\rangle - 1$
. We call
![]() $\operatorname {\mathrm {pr}}_{p/q}(xy, z)$
a primitive exceptional intersection word of the second type if the following hold:
$\operatorname {\mathrm {pr}}_{p/q}(xy, z)$
a primitive exceptional intersection word of the second type if the following hold:
-
(1)
 $\langle z\rangle $
is malnormal.
$\langle z\rangle $
is malnormal. -
(2) If
 $p/q = k\in \mathbb {N}$
, then there is no
$p/q = k\in \mathbb {N}$
, then there is no
 $a\in \langle A, B\rangle - \langle B\rangle $
,
$a\in \langle A, B\rangle - \langle B\rangle $
,
 $c\in \langle B, C\rangle - \langle B\rangle $
such that
$c\in \langle B, C\rangle - \langle B\rangle $
such that
 $\operatorname {\mathrm {pr}}_{k}(xy, z) = \operatorname {\mathrm {pr}}_{1}(a, c)$
and
$\operatorname {\mathrm {pr}}_{k}(xy, z) = \operatorname {\mathrm {pr}}_{1}(a, c)$
and
 $\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family.
$\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family.
By definition, we see that
![]() $\langle xy, z\rangle $
is an infinite cyclic subgroup of
$\langle xy, z\rangle $
is an infinite cyclic subgroup of
![]() $G = F(A, B, C)/\langle \langle w \rangle \rangle $
and so
$G = F(A, B, C)/\langle \langle w \rangle \rangle $
and so
![]() $(xy)^{-1}z(xy) =_G z$
. We find that G has the following exceptional intersection:
$(xy)^{-1}z(xy) =_G z$
. We find that G has the following exceptional intersection:
A word
![]() $w\in F(A, B, C)$
is a primitive exceptional intersection word if w is a primitive exceptional intersection word of the first or second type.
$w\in F(A, B, C)$
is a primitive exceptional intersection word if w is a primitive exceptional intersection word of the first or second type.
Definition 3.2 A group G is a primitive exceptional intersection group if
![]() $G\cong F(\Sigma )/\langle \langle w \rangle \rangle $
where w is a primitive exceptional intersection word.
$G\cong F(\Sigma )/\langle \langle w \rangle \rangle $
where w is a primitive exceptional intersection word.
Example 3.4 Consider the word
![]() $\operatorname {\mathrm {pr}}_{k}(a^2b^2c^2, b) = a^2b^2c^2b^k\in F(a, b, c)$
. Since this is equal to
$\operatorname {\mathrm {pr}}_{k}(a^2b^2c^2, b) = a^2b^2c^2b^k\in F(a, b, c)$
. Since this is equal to
![]() $\operatorname {\mathrm {pr}}_{1}(a^2b^{2-k}, b^{-k}c^2b^k)$
where
$\operatorname {\mathrm {pr}}_{1}(a^2b^{2-k}, b^{-k}c^2b^k)$
where
![]() $\langle b^{-k}c^2b^k\rangle $
is not malnormal, it is not a primitive exceptional intersection word of the second type. However, it is also equal to the word
$\langle b^{-k}c^2b^k\rangle $
is not malnormal, it is not a primitive exceptional intersection word of the second type. However, it is also equal to the word
![]() $\operatorname {\mathrm {pr}}_{2}(a^2b^{2-k}, b^{-k}cb^k)$
(or
$\operatorname {\mathrm {pr}}_{2}(a^2b^{2-k}, b^{-k}cb^k)$
(or
![]() $\operatorname {\mathrm {pr}}_{1/2}(a, b^2c^2b^2)$
when
$\operatorname {\mathrm {pr}}_{1/2}(a, b^2c^2b^2)$
when
![]() $k = 2$
) which is a primitive exceptional intersection word of the first type. Thus,
$k = 2$
) which is a primitive exceptional intersection word of the first type. Thus,
is a primitive exceptional intersection group for all k.
The proof of the following theorem is rather involved and will take up the remainder of this section.
Theorem 3.5 Primitive exceptional intersection groups are
![]() $2$
-free.
$2$
-free.
Before proceeding with the proof, we mention some important definitions and a result from [Reference Louder and WiltonLW22]. Define the primitivity rank of an element
![]() $w\in F(\Sigma )$
as the following quantity:
$w\in F(\Sigma )$
as the following quantity:
Given an element
![]() $w\in F(\Sigma )$
such that
$w\in F(\Sigma )$
such that
![]() $\pi (w)<\infty $
, a subgroup
$\pi (w)<\infty $
, a subgroup
![]() $K<F(\Sigma )$
is a w-subgroup if the following hold:
$K<F(\Sigma )$
is a w-subgroup if the following hold:
-
(1)
 $w\in K$
and w is not primitive in K.
$w\in K$
and w is not primitive in K. -
(2)
 $\operatorname {\mathrm {rk}}(K) = \pi (w)$
.
$\operatorname {\mathrm {rk}}(K) = \pi (w)$
. -
(3) If
 $K<K'$
, then
$K<K'$
, then
 $\operatorname {\mathrm {rk}}(K)<\operatorname {\mathrm {rk}}(K')$
.
$\operatorname {\mathrm {rk}}(K)<\operatorname {\mathrm {rk}}(K')$
.
In [Reference Louder and WiltonLW22], Louder and Wilton connect the primitivity rank
![]() $\pi (w)$
with subgroup properties of the one-relator group
$\pi (w)$
with subgroup properties of the one-relator group
![]() $F(\Sigma )/\langle \langle w \rangle \rangle $
. The result we shall need is the following, appearing as [Reference Louder and WiltonLW22, Theorem 1.5].
$F(\Sigma )/\langle \langle w \rangle \rangle $
. The result we shall need is the following, appearing as [Reference Louder and WiltonLW22, Theorem 1.5].
Theorem 3.6 A one-relator group
![]() $F(\Sigma )/\langle \langle w \rangle \rangle $
is
$F(\Sigma )/\langle \langle w \rangle \rangle $
is
![]() $2$
-free if and only if
$2$
-free if and only if
![]() $\pi (w)>2$
.
$\pi (w)>2$
.
The idea of the proof of Theorem 3.5 will then be to show that if
![]() $w\in F(\Sigma )$
is a primitive exceptional intersection word, then there cannot be any two-generator w-subgroups.
$w\in F(\Sigma )$
is a primitive exceptional intersection word, then there cannot be any two-generator w-subgroups.
Proof of Theorem 3.5
If G is a primitive exceptional intersection group, then there is a free group
![]() $F(A, B, C)$
, a rational number
$F(A, B, C)$
, a rational number
![]() $p/q\in \mathbb {Q}_{>0}$
, and elements
$p/q\in \mathbb {Q}_{>0}$
, and elements
 $$ \begin{align*} x &\in \langle A, B\rangle - \langle B\rangle~,\\ y &\in \langle B, C\rangle - \langle B\rangle~,\\ z &\in \langle B\rangle - 1~, \end{align*} $$
$$ \begin{align*} x &\in \langle A, B\rangle - \langle B\rangle~,\\ y &\in \langle B, C\rangle - \langle B\rangle~,\\ z &\in \langle B\rangle - 1~, \end{align*} $$
such that
![]() $G\cong F(A, B, C)/\langle \langle w \rangle \rangle $
where one of the following holds:
$G\cong F(A, B, C)/\langle \langle w \rangle \rangle $
where one of the following holds:
-
(1)
 $w = \operatorname {\mathrm {pr}}_{p/q}(x, y)$
is a primitive exceptional intersection word of the first type.
$w = \operatorname {\mathrm {pr}}_{p/q}(x, y)$
is a primitive exceptional intersection word of the first type. -
(2)
 $w = \operatorname {\mathrm {pr}}_{p/q}(xy, z)$
is a primitive exceptional intersection word of the second type.
$w = \operatorname {\mathrm {pr}}_{p/q}(xy, z)$
is a primitive exceptional intersection word of the second type.
Let us assume for the sake of contradiction that G is not
![]() $2$
-free. Then, by Corollary 3.2 and Theorem 3.6, we have that
$2$
-free. Then, by Corollary 3.2 and Theorem 3.6, we have that
![]() $\pi (w) = 2$
. Thus, there is some w-subgroup
$\pi (w) = 2$
. Thus, there is some w-subgroup
![]() ${K<F(A, B, C)}$
such that
${K<F(A, B, C)}$
such that
![]() $\operatorname {\mathrm {rk}}(K) = 2$
. We will handle the two cases at the same time as they are very similar.
$\operatorname {\mathrm {rk}}(K) = 2$
. We will handle the two cases at the same time as they are very similar.
Let
![]() $\Delta $
be a rose graph with one edge for each element in
$\Delta $
be a rose graph with one edge for each element in
![]() $A\sqcup B\sqcup C$
. The edges of
$A\sqcup B\sqcup C$
. The edges of
![]() $\Delta $
can then be partitioned into A-edges, B-edges, and C-edges. Denote by
$\Delta $
can then be partitioned into A-edges, B-edges, and C-edges. Denote by
![]() $\omega :S^1\looparrowright \Delta $
the cycle representing w. There is an immersion of core graphs
$\omega :S^1\looparrowright \Delta $
the cycle representing w. There is an immersion of core graphs
![]() $\Lambda \looparrowright \Delta $
representing the conjugacy class of K such that there is a lift
$\Lambda \looparrowright \Delta $
representing the conjugacy class of K such that there is a lift
![]() $\lambda :S^1\looparrowright \Lambda $
of
$\lambda :S^1\looparrowright \Lambda $
of
![]() $\omega $
. Now let
$\omega $
. Now let
![]() $\Gamma \looparrowright \Delta $
be the graph immersion of core graphs representing the conjugacy class of
$\Gamma \looparrowright \Delta $
be the graph immersion of core graphs representing the conjugacy class of
![]() $\langle x, y\rangle <\pi _1(\Delta )$
(or
$\langle x, y\rangle <\pi _1(\Delta )$
(or
![]() $\langle xy, z\rangle $
if we are in the second case). Then there is a lift
$\langle xy, z\rangle $
if we are in the second case). Then there is a lift
![]() $\gamma :S^1\looparrowright \Gamma $
of
$\gamma :S^1\looparrowright \Gamma $
of
![]() $\omega $
.
$\omega $
.
Lemma 3.7 There is some connected component
![]() $\Theta \subset \operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
such that
$\Theta \subset \operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
such that
![]() $\Theta \cong S^1$
and
$\Theta \cong S^1$
and
![]() $\lambda = p_{\Lambda }\mid \Theta $
.
$\lambda = p_{\Lambda }\mid \Theta $
.
Proof By [Reference KentKen09, Theorem 1] (see also [Reference Louder and McReynoldsLM09, Theorem 1.1]), either
![]() $\chi (\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )) = 0$
, or
$\chi (\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )) = 0$
, or
![]() $\operatorname {\mathrm {rk}}(\langle \pi _1(\Lambda )^g,\pi _1(\Gamma )\rangle ) = 2$
for some
$\operatorname {\mathrm {rk}}(\langle \pi _1(\Lambda )^g,\pi _1(\Gamma )\rangle ) = 2$
for some
![]() $g\in \pi _1(\Delta )$
. In the first case, we must have that
$g\in \pi _1(\Delta )$
. In the first case, we must have that
![]() $\lambda $
factors through some component
$\lambda $
factors through some component
![]() $S^1\subset \operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
. Since G is torsion-free, w cannot be a proper power by [Reference Karrass, Magnus and SolitarKMS60]. Therefore,
$S^1\subset \operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
. Since G is torsion-free, w cannot be a proper power by [Reference Karrass, Magnus and SolitarKMS60]. Therefore,
![]() $\omega $
and
$\omega $
and
![]() $\lambda $
cannot factor through
$\lambda $
cannot factor through
![]() $S^1$
as a proper cover and we are done.
$S^1$
as a proper cover and we are done.
Now suppose that
![]() $\operatorname {\mathrm {rk}}(\langle \pi _1(\Lambda )^g,\pi _1(\Gamma )\rangle ) = 2$
. By definition of w-subgroups, we must have that
$\operatorname {\mathrm {rk}}(\langle \pi _1(\Lambda )^g,\pi _1(\Gamma )\rangle ) = 2$
. By definition of w-subgroups, we must have that
![]() $\pi _1(\Gamma )<\pi _1(\Lambda )^g$
. Now it follows from our assumptions on
$\pi _1(\Gamma )<\pi _1(\Lambda )^g$
. Now it follows from our assumptions on
![]() $x, y, z$
and Lemmas 2.3 and 2.4, that
$x, y, z$
and Lemmas 2.3 and 2.4, that
![]() $\pi _1(\Gamma ) = \pi _1(\Lambda )^g$
, contradicting the fact that w is not primitive in K.
$\pi _1(\Gamma ) = \pi _1(\Lambda )^g$
, contradicting the fact that w is not primitive in K.
We will make use of the following factorizations of x and y:
 $$ \begin{align*} x &= b_1\cdot x_1^{-1}\cdot x_2\cdot x_1\cdot b_2~,\\ y &= b_3\cdot y_1^{-1}\cdot y_2\cdot y_1\cdot b_4~, \end{align*} $$
$$ \begin{align*} x &= b_1\cdot x_1^{-1}\cdot x_2\cdot x_1\cdot b_2~,\\ y &= b_3\cdot y_1^{-1}\cdot y_2\cdot y_1\cdot b_4~, \end{align*} $$
as freely reduced words, where
![]() $b_1, b_2, b_3, b_4\in \langle B\rangle $
,
$b_1, b_2, b_3, b_4\in \langle B\rangle $
,
![]() $x_1^{-1}\cdot x_2\cdot x_1$
and
$x_1^{-1}\cdot x_2\cdot x_1$
and
![]() $y_1^{-1}\cdot y_2\cdot y_1$
do not begin or end with a B-letter and
$y_1^{-1}\cdot y_2\cdot y_1$
do not begin or end with a B-letter and
![]() $x_2$
and
$x_2$
and
![]() $y_2$
are cyclically reduced.
$y_2$
are cyclically reduced.
If
![]() $n\geq 1$
, denote by
$n\geq 1$
, denote by
![]() $u_n$
the free reduction of
$u_n$
the free reduction of
![]() $x_1^{-1}x_2x_1(b_2b_1x_1^{-1}x_2x_1)^{n-1}$
. Similarly, denote by
$x_1^{-1}x_2x_1(b_2b_1x_1^{-1}x_2x_1)^{n-1}$
. Similarly, denote by
![]() $v_n$
the free reduction of
$v_n$
the free reduction of
![]() $y_1^{-1}y_2y_1(b_4b_3y_1^{-1}y_2y_1)^{n-1}$
.
$y_1^{-1}y_2y_1(b_4b_3y_1^{-1}y_2y_1)^{n-1}$
.
Lemma 3.8 Let
![]() $n\geq 1$
, and let
$n\geq 1$
, and let
![]() $\alpha :I\looparrowright \Lambda $
be a path labeled by
$\alpha :I\looparrowright \Lambda $
be a path labeled by
![]() $u_n$
or
$u_n$
or
![]() $v_n$
. Then
$v_n$
. Then
![]() $\alpha $
must traverse a vertex of degree at least three, other than at its endpoints.
$\alpha $
must traverse a vertex of degree at least three, other than at its endpoints.
Proof We shall prove the result for
![]() $u_n$
as the other case is identical. First, we show that
$u_n$
as the other case is identical. First, we show that
![]() $\Gamma $
supports at most one path with label
$\Gamma $
supports at most one path with label
![]() $u_n$
. If
$u_n$
. If
![]() $\pi _1(\Gamma ) = \langle xy, z\rangle $
, then
$\pi _1(\Gamma ) = \langle xy, z\rangle $
, then
![]() $\Gamma $
supports one path with label
$\Gamma $
supports one path with label
![]() $u_1$
and no path with label
$u_1$
and no path with label
![]() $u_k$
for any
$u_k$
for any
![]() $k\geq 2$
. Let us suppose that
$k\geq 2$
. Let us suppose that
![]() $\pi _1(\Gamma ) = \langle x, y\rangle $
and that there are two paths in
$\pi _1(\Gamma ) = \langle x, y\rangle $
and that there are two paths in
![]() $\Gamma $
with label
$\Gamma $
with label
![]() $u_n$
. Since
$u_n$
. Since
![]() $u_n$
begins and ends with an A-letter and does not contain any C-letters, it follows that:
$u_n$
begins and ends with an A-letter and does not contain any C-letters, it follows that:
-
(1) If
 $b_2b_1\neq 1$
or
$b_2b_1\neq 1$
or
 $b_2b_1 = x_1 = 1$
, then
$b_2b_1 = x_1 = 1$
, then
 $u_n$
must be a subword of
$u_n$
must be a subword of
 $u_{n+1}$
that is not a prefix or a suffix, or
$u_{n+1}$
that is not a prefix or a suffix, or
 $u_n$
is a subword of
$u_n$
is a subword of
 $u_{n+1}^{-1}$
.
$u_{n+1}^{-1}$
. -
(2) If
 $b_2b_1 = 1$
and
$b_2b_1 = 1$
and
 $x_1 \neq 1$
, then
$x_1 \neq 1$
, then
 $u_n$
must be a subword of
$u_n$
must be a subword of
 $u_{m}^{\pm 1}$
for some
$u_{m}^{\pm 1}$
for some
 $m>n$
.
$m>n$
.
Since
![]() $\langle x\rangle $
is malnormal by definition, x is not a proper power. The first situation cannot happen by Lemma 2.2. The second situation cannot happen by Lemma 2.1.
$\langle x\rangle $
is malnormal by definition, x is not a proper power. The first situation cannot happen by Lemma 2.2. The second situation cannot happen by Lemma 2.1.
Now, since there is at most one path in
![]() $\Gamma $
with label
$\Gamma $
with label
![]() $u_n$
, there can be at most one lift of
$u_n$
, there can be at most one lift of
![]() $\alpha $
to
$\alpha $
to
![]() $\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
by definition of the fiber product graph. If
$\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
by definition of the fiber product graph. If
![]() $\alpha $
does not traverse vertices of degree three or more, except possibly at its endpoints, then each edge it traverses can have at most one preimage in
$\alpha $
does not traverse vertices of degree three or more, except possibly at its endpoints, then each edge it traverses can have at most one preimage in
![]() $\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
. So, by Lemma 3.7, since
$\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
. So, by Lemma 3.7, since
![]() $\lambda $
is surjective, it must traverse some edge in
$\lambda $
is surjective, it must traverse some edge in
![]() $\Lambda $
precisely once. But then this would imply that
$\Lambda $
precisely once. But then this would imply that
![]() $\lambda $
represents a primitive element of
$\lambda $
represents a primitive element of
![]() $\pi _1(\Lambda )$
, contradicting the fact that K was a w-subgroup. Therefore, we conclude that
$\pi _1(\Lambda )$
, contradicting the fact that K was a w-subgroup. Therefore, we conclude that
![]() $\alpha $
must traverse a vertex of degree at least three, other than at its endpoints.
$\alpha $
must traverse a vertex of degree at least three, other than at its endpoints.
We now use Lemma 3.8 to derive a contradiction to the definitions of primitive exceptional intersection words. Let
![]() $\alpha :I\looparrowright \Lambda $
be a path satisfying the following:
$\alpha :I\looparrowright \Lambda $
be a path satisfying the following:
-
(1)
 $\alpha $
factors through
$\alpha $
factors through
 $\lambda $
.
$\lambda $
. -
(2)
 $\alpha $
is labeled by
$\alpha $
is labeled by
 $u_n$
for some
$u_n$
for some
 $n> 0$
.
$n> 0$
. -
(3) There is no path
 $\alpha ':I\looparrowright \Lambda $
, strictly extending
$\alpha ':I\looparrowright \Lambda $
, strictly extending
 $\alpha $
and satisfying the above.
$\alpha $
and satisfying the above.
We similarly define
![]() $\beta :I\looparrowright \Lambda $
, replacing
$\beta :I\looparrowright \Lambda $
, replacing
![]() $u_n$
with
$u_n$
with
![]() $v_n$
. Such paths exist by definition of w.
$v_n$
. Such paths exist by definition of w.
By Lemma 3.8,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
must traverse a vertex of degree at least three, away from their endpoints. Now the idea is to use this fact to divide
$\beta $
must traverse a vertex of degree at least three, away from their endpoints. Now the idea is to use this fact to divide
![]() $\Lambda $
according to where
$\Lambda $
according to where
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
are supported. Since
$\beta $
are supported. Since
![]() $\alpha $
does not traverse any C-edges and
$\alpha $
does not traverse any C-edges and
![]() $\beta $
does not traverse any A-edges, they will block each other from traversing certain regions of
$\beta $
does not traverse any A-edges, they will block each other from traversing certain regions of
![]() $\Lambda $
.
$\Lambda $
.
Since
![]() $\chi (\Lambda ) = -1$
, and
$\chi (\Lambda ) = -1$
, and
![]() $\Lambda $
is a core graph, we only have three topologically distinct cases to consider:
$\Lambda $
is a core graph, we only have three topologically distinct cases to consider:
-
(1)
 $\Lambda $
is a rose graph (see Figure 2).
$\Lambda $
is a rose graph (see Figure 2).
Figure 2: Rose graph cases.
-
(2)
 $\Lambda $
is a theta graph (see Figure 3).
$\Lambda $
is a theta graph (see Figure 3).
Figure 3: Theta graph cases.

Figure 4: Extra theta cases.
-
(3)
 $\Lambda $
is a spectacles graph (see Figure 5).
$\Lambda $
is a spectacles graph (see Figure 5).
Figure 5: Spectacles graph cases.
Figures 2, 3, and 5 contain all the different cases, up to symmetry. Before proceeding with the case analysis, we briefly explain the diagrams. The red regions indicate sections that
![]() $\alpha $
traverses and must contain an A-edge;
$\alpha $
traverses and must contain an A-edge;
![]() $\beta $
cannot traverse any edge in a red region. The blue regions indicate sections that
$\beta $
cannot traverse any edge in a red region. The blue regions indicate sections that
![]() $\beta $
traverses and must contain a C-edge;
$\beta $
traverses and must contain a C-edge;
![]() $\alpha $
cannot traverse any edge in a blue region. The yellow regions indicate sections that
$\alpha $
cannot traverse any edge in a blue region. The yellow regions indicate sections that
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
or both
$\beta $
or both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
traverse. In any case, the yellow regions must only contain B-edges, but are allowed to have length zero when this does not change the topology of the underlying graph. The black regions indicate sections that are not traversed by either
$\beta $
traverse. In any case, the yellow regions must only contain B-edges, but are allowed to have length zero when this does not change the topology of the underlying graph. The black regions indicate sections that are not traversed by either
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
and are also allowed to have length zero when this does not change the topology of the underlying graph. The red vertices and blue vertices indicate the start and endpoints of
$\beta $
and are also allowed to have length zero when this does not change the topology of the underlying graph. The red vertices and blue vertices indicate the start and endpoints of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, respectively.
$\beta $
, respectively.
Topologically, in each diagram, there can be at most three edges. The path
![]() $\alpha $
must leave one of these edges by Lemma 3.8 and reenter another edge, leaving enough space for
$\alpha $
must leave one of these edges by Lemma 3.8 and reenter another edge, leaving enough space for
![]() $\beta $
to do the same elsewhere. Given these constraints, the reader should check that these are indeed all the cases to consider.
$\beta $
to do the same elsewhere. Given these constraints, the reader should check that these are indeed all the cases to consider.
Case 1 We handle this case more in detail than the others as the arguments are mostly identical. We have three subcases to consider, according to Figure 2.
Suppose we are in the situation of the first subdiagram. When
![]() $\lambda $
traverses a red segment from a red vertex, it must then be followed by the other red segment. Otherwise, we would obtain a contradiction to Lemma 3.8. Similarly for the blue segments. Thus, since
$\lambda $
traverses a red segment from a red vertex, it must then be followed by the other red segment. Otherwise, we would obtain a contradiction to Lemma 3.8. Similarly for the blue segments. Thus, since
![]() $\lambda $
is primitive, it must traverse each edge precisely once. Hence,
$\lambda $
is primitive, it must traverse each edge precisely once. Hence,
![]() $\lambda $
would not represent a primitive element of
$\lambda $
would not represent a primitive element of
![]() $\pi _1(\Lambda )$
which is a contradiction.
$\pi _1(\Lambda )$
which is a contradiction.
Now consider the second subdiagram. Any (maximal)
![]() $u_n$
labeled path must begin at one red vertex and end at the other red vertex. Similarly for the
$u_n$
labeled path must begin at one red vertex and end at the other red vertex. Similarly for the
![]() $v_n$
labeled paths. But this then implies that only one power of x and one power of y appears in w. Thus, if w is of the first type, then it must be equal to
$v_n$
labeled paths. But this then implies that only one power of x and one power of y appears in w. Thus, if w is of the first type, then it must be equal to
![]() $xy$
. If w is of the second type, it must be equal to
$xy$
. If w is of the second type, it must be equal to
![]() $xyz^i$
for some
$xyz^i$
for some
![]() $i\geq 1$
. By Lemma 3.8,
$i\geq 1$
. By Lemma 3.8,
![]() $\lambda $
must traverse both loops at least twice. We may now deduce that there exist elements:
$\lambda $
must traverse both loops at least twice. We may now deduce that there exist elements:
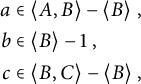 $$ \begin{align*} a &\in \langle A, B\rangle - \langle B\rangle~,\\ b &\in \langle B\rangle - 1~,\\ c &\in \langle B, C\rangle - \langle B\rangle~, \end{align*} $$
$$ \begin{align*} a &\in \langle A, B\rangle - \langle B\rangle~,\\ b &\in \langle B\rangle - 1~,\\ c &\in \langle B, C\rangle - \langle B\rangle~, \end{align*} $$
such that
![]() $w = (ab^{-1})(bc)$
and that
$w = (ab^{-1})(bc)$
and that
![]() $\pi (a), \pi (c)\neq 1$
. Hence,
$\pi (a), \pi (c)\neq 1$
. Hence,
![]() $\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family, contradicting our assumptions on w.
$\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family, contradicting our assumptions on w.
Let us move onto the third subdiagram. Similarly to the second subcase, we see that if w is of the first type, it must be equal to
![]() $xy$
and if w is of the second type, it must be equal to
$xy$
and if w is of the second type, it must be equal to
![]() $xyz^i$
for some
$xyz^i$
for some
![]() $i\geq 1$
. From the diagram, we may now deduce that there exist elements:
$i\geq 1$
. From the diagram, we may now deduce that there exist elements:
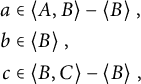 $$ \begin{align*} a &\in \langle A, B\rangle - \langle B\rangle~,\\ b &\in \langle B\rangle~,\\ c &\in \langle B, C\rangle - \langle B\rangle~, \end{align*} $$
$$ \begin{align*} a &\in \langle A, B\rangle - \langle B\rangle~,\\ b &\in \langle B\rangle~,\\ c &\in \langle B, C\rangle - \langle B\rangle~, \end{align*} $$
such that
![]() $w = (ab^{-1})(bc)$
and that
$w = (ab^{-1})(bc)$
and that
![]() $\langle a\rangle ^g\cap \langle c\rangle \neq 1$
for some
$\langle a\rangle ^g\cap \langle c\rangle \neq 1$
for some
![]() $g\in F(A, B, C)$
. Hence,
$g\in F(A, B, C)$
. Hence,
![]() $\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family, contradicting our assumptions on w. It follows that
$\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family, contradicting our assumptions on w. It follows that
![]() $\Lambda $
cannot be a rose graph.
$\Lambda $
cannot be a rose graph.
Case 2 Consider the first subdiagram in Figure 3. By collapsing the yellow edge, we see that we may handle this case in the same way as the first subcase of the rose case. Similarly, we may reduce the second and third subcases to the second and third subcases of the rose case.
So now let us consider the new cases appearing in the fourth and fifth subdiagrams. Now if
![]() $b_2b_1\neq 1$
and
$b_2b_1\neq 1$
and
![]() $\alpha $
was labeled by
$\alpha $
was labeled by
![]() $u_n$
with
$u_n$
with
![]() $n\geq 2$
, then we would have that
$n\geq 2$
, then we would have that
![]() $\Lambda $
would support a path labeled by
$\Lambda $
would support a path labeled by
![]() $u_1$
that does not traverse a vertex of degree at least three, away from its endpoints. But this contradicts Lemma 3.8. So if
$u_1$
that does not traverse a vertex of degree at least three, away from its endpoints. But this contradicts Lemma 3.8. So if
![]() $b_2b_1 \neq 1$
and
$b_2b_1 \neq 1$
and
![]() $n=1$
, then there can be no other
$n=1$
, then there can be no other
![]() $u_m$
-labeled path beginning or ending at a red vertex as
$u_m$
-labeled path beginning or ending at a red vertex as
![]() $\Lambda \looparrowright \Delta $
is an immersion. This would imply that there can be no other
$\Lambda \looparrowright \Delta $
is an immersion. This would imply that there can be no other
![]() $u_m$
-labeled paths in
$u_m$
-labeled paths in
![]() $\Lambda $
for any
$\Lambda $
for any
![]() $m\geq 1$
and so
$m\geq 1$
and so
![]() $\lambda $
traverses the red segments only once by Lemma 3.7. Hence,
$\lambda $
traverses the red segments only once by Lemma 3.7. Hence,
![]() $\lambda $
could not represent a primitive element of
$\lambda $
could not represent a primitive element of
![]() $\pi _1(\Lambda )$
, a contradiction. So now we may assume that
$\pi _1(\Lambda )$
, a contradiction. So now we may assume that
![]() $b_2b_1 = 1$
. By a symmetric argument, we may assume that
$b_2b_1 = 1$
. By a symmetric argument, we may assume that
![]() $b_4b_3 = 1$
. Similarly, we must have
$b_4b_3 = 1$
. Similarly, we must have
![]() $x_1, y_1\neq 1$
. As before, there must be at least one other path
$x_1, y_1\neq 1$
. As before, there must be at least one other path
![]() $\alpha ':I\looparrowright \Lambda $
labeled by
$\alpha ':I\looparrowright \Lambda $
labeled by
![]() $u_m$
for some
$u_m$
for some
![]() $m\geq 1$
. We may assume that
$m\geq 1$
. We may assume that
![]() $\alpha '$
is maximal in the same sense that
$\alpha '$
is maximal in the same sense that
![]() $\alpha $
was maximal. We see that
$\alpha $
was maximal. We see that
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
must traverse a common segment. We now have two subcases to consider, up to symmetry, depending on whether
$\alpha '$
must traverse a common segment. We now have two subcases to consider, up to symmetry, depending on whether
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
traverse a common segment in the same direction or the opposite direction. See Figure 4. In either case, there can only be one lift of the segment with label
$\alpha '$
traverse a common segment in the same direction or the opposite direction. See Figure 4. In either case, there can only be one lift of the segment with label
![]() $x_2^mx_1$
to
$x_2^mx_1$
to
![]() $\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
for the following reason: the projection of any loop in
$\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
for the following reason: the projection of any loop in
![]() $\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
traversing the segment labeled
$\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
traversing the segment labeled
![]() $x_2^mx_1$
, must then traverse a blue segment labeled by
$x_2^mx_1$
, must then traverse a blue segment labeled by
![]() $y_1^{-1}y_2^k$
for some
$y_1^{-1}y_2^k$
for some
![]() $k\geq 0$
. Since there is only one path in
$k\geq 0$
. Since there is only one path in
![]() $\Gamma $
with this label, there can be only one lift of these segments to
$\Gamma $
with this label, there can be only one lift of these segments to
![]() $\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
. Now Lemma 3.7 tells us that
$\operatorname {\mathrm {Core}}(\Gamma \times _{\Delta }\Lambda )$
. Now Lemma 3.7 tells us that
![]() $\lambda $
does not represent a primitive element of
$\lambda $
does not represent a primitive element of
![]() $\pi _1(\Lambda )$
. It follows that
$\pi _1(\Lambda )$
. It follows that
![]() $\Lambda $
cannot be a theta graph.
$\Lambda $
cannot be a theta graph.
Case 3 The first subdiagram in Figure 5 is analogous to the first subdiagram of the rose case. The second, third, and fourth subdiagrams are analogous to the second subdiagram of the rose case. The fifth subdiagram is analogous to the third subdiagram of the rose case. Hence,
![]() $\Lambda $
cannot be a spectacles graph.
$\Lambda $
cannot be a spectacles graph.
Now we may conclude that there can be no w-subgroups of rank two and, hence, G must be
![]() $2$
-free.
$2$
-free.
3.2 The general case
In this section, we consider the general case and show that primitive exceptional intersection groups are the only exceptional intersection groups which are
![]() $2$
-free.
$2$
-free.
Theorem 3.1 was generalized to one-relator products in [Reference HowieHow05]. By specializing [Reference HowieHow05, Theorem C] to the case of one-relator groups, we may obtain the following result.
Theorem 3.9 Let
![]() $F(\Sigma )/\langle \langle w \rangle \rangle $
be a one-relator group and suppose
$F(\Sigma )/\langle \langle w \rangle \rangle $
be a one-relator group and suppose
![]() $\Sigma = A\sqcup B\sqcup C$
. If
$\Sigma = A\sqcup B\sqcup C$
. If
![]() $\langle A, B\rangle $
and
$\langle A, B\rangle $
and
![]() $\langle B, C\rangle $
are Magnus subgroups with exceptional intersection, then there is a monomorphism of free groups
$\langle B, C\rangle $
are Magnus subgroups with exceptional intersection, then there is a monomorphism of free groups
with the following properties. There is some
![]() $r\in F(a, c)$
with
$r\in F(a, c)$
with
![]() $\iota (r)$
conjugate to w and some
$\iota (r)$
conjugate to w and some
![]() $m, n\neq 0$
, such that one of the following holds:
$m, n\neq 0$
, such that one of the following holds:
-
(1)
 $a^m = c^n$
in
$a^m = c^n$
in
 $F(a, c)/\langle \langle r \rangle \rangle $
with
$F(a, c)/\langle \langle r \rangle \rangle $
with
 $\iota (a) = x$
,
$\iota (a) = x$
,
 $\iota (c) = y$
and
$\iota (c) = y$
and  $$ \begin{align*} x\in \langle A, B\rangle - \langle B\rangle~,\\ y\in \langle B, C\rangle - \langle B\rangle~. \end{align*} $$
$$ \begin{align*} x\in \langle A, B\rangle - \langle B\rangle~,\\ y\in \langle B, C\rangle - \langle B\rangle~. \end{align*} $$
-
(2)
 $ac^ma^{-1} = c^n$
in
$ac^ma^{-1} = c^n$
in
 $F(a, c)/\langle \langle r \rangle \rangle $
with
$F(a, c)/\langle \langle r \rangle \rangle $
with
 $\iota (a) = xy$
,
$\iota (a) = xy$
,
 $\iota (c) = z$
and
$\iota (c) = z$
and  $$ \begin{align*} x& \in \langle A, B\rangle - \langle B\rangle~,\\ y & \in\langle B, C\rangle - \langle B\rangle~,\\ z & \in \langle B\rangle - 1~. \end{align*} $$
$$ \begin{align*} x& \in \langle A, B\rangle - \langle B\rangle~,\\ y & \in\langle B, C\rangle - \langle B\rangle~,\\ z & \in \langle B\rangle - 1~. \end{align*} $$
Using this result and the algorithm to compute the center of a one-relator group from [Reference Baumslag and TaylorBT68], Howie also showed that a generating set for the intersection of given Magnus subgroups is computable [Reference HowieHow05, Theorem E].
In the discussion following [Reference CollinsCol04, Theorem 4], Collins points out the following.
Corollary 3.10 Assume the notation of Theorem 3.9 and suppose that we are in the first case. Denote by
Then we have
Corollary 3.11 Assume the notation of Theorem 3.9 and suppose that we are in the second case. Let
![]() $\iota (a) = x\cdot y$
where
$\iota (a) = x\cdot y$
where
![]() $x\in \langle A, B\rangle - \langle B\rangle $
and
$x\in \langle A, B\rangle - \langle B\rangle $
and
![]() $y \in \langle B, C\rangle - \langle B\rangle $
and denote by
$y \in \langle B, C\rangle - \langle B\rangle $
and denote by
Then we have
Remark 3.12 There is a minor typographical error in the splitting provided by Collins for the second case. Corollary 3.11 is the corrected version.
The following follows directly from Corollaries 3.10 and 3.11.
Corollary 3.13 Assume the notation of Theorem 3.9. The monomorphism
![]() $\iota $
descends to a monomorphism of one-relator groups:
$\iota $
descends to a monomorphism of one-relator groups:
Theorem 3.9, coupled with Corollary 3.13, finds us two-generator one-relator subgroups of exceptional intersection groups. We now characterize precisely what these subgroups can be.
Lemma 3.14 Let
![]() $H = F(a, c)/\langle \langle r \rangle \rangle $
be torsion-free such that
$H = F(a, c)/\langle \langle r \rangle \rangle $
be torsion-free such that
![]() $a^m = c^n$
in H for some
$a^m = c^n$
in H for some
![]() $m, n\neq 0$
. Then one of the following hold:
$m, n\neq 0$
. Then one of the following hold:
-
(1)
 $r\in F(a, c)$
is primitive and so
$r\in F(a, c)$
is primitive and so
 $H\cong \mathbb {Z}$
.
$H\cong \mathbb {Z}$
. -
(2) H is noncyclic with nontrivial center.
Proof Note that H has nontrivial center as
![]() $\langle a^m\rangle $
is an infinite subgroup contained in the center. By [Reference Lyndon and SchuppLS01, Chapter II, Proposition 5.11], H is cyclic if and only if r is primitive.
$\langle a^m\rangle $
is an infinite subgroup contained in the center. By [Reference Lyndon and SchuppLS01, Chapter II, Proposition 5.11], H is cyclic if and only if r is primitive.
Lemma 3.15 Let
![]() $H = F(a, c)/\langle \langle r \rangle \rangle $
be torsion-free such that
$H = F(a, c)/\langle \langle r \rangle \rangle $
be torsion-free such that
![]() $a^{-1}c^ma = c^n$
in H for some
$a^{-1}c^ma = c^n$
in H for some
![]() $m, n\neq 0$
. Then one of the following hold:
$m, n\neq 0$
. Then one of the following hold:
-
(1)
 $r\in F(a, c)$
is primitive and so
$r\in F(a, c)$
is primitive and so
 $H\cong \mathbb {Z}$
.
$H\cong \mathbb {Z}$
. -
(2) H is noncyclic with nontrivial center.
-
(3) r or
 $r^{-1}$
is conjugate to
$r^{-1}$
is conjugate to
 $\operatorname {\mathrm {pr}}_{p/q}(c^{-1}, a^{-1}ca)$
for some
$\operatorname {\mathrm {pr}}_{p/q}(c^{-1}, a^{-1}ca)$
for some
 $p/q\in \mathbb {Q}_{>0}$
and so
$p/q\in \mathbb {Q}_{>0}$
and so
 $H\cong BS(p, q)$
.
$H\cong BS(p, q)$
. -
(4) r or
 $r^{-1}$
is conjugate in
$r^{-1}$
is conjugate in
 $F(a, c)$
to an element
$F(a, c)$
to an element
 $r'\in \langle c, a^{-1}ca\rangle $
such that
$r'\in \langle c, a^{-1}ca\rangle $
such that
 $\langle c, a^{-1}ca\rangle \cong F(c, a^{-1}ca)/\langle \langle r' \rangle \rangle $
is noncyclic with nontrivial center.
$\langle c, a^{-1}ca\rangle \cong F(c, a^{-1}ca)/\langle \langle r' \rangle \rangle $
is noncyclic with nontrivial center.
Proof Suppose that
![]() ${\lvert {m} \rvert }$
is smallest possible. If
${\lvert {m} \rvert }$
is smallest possible. If
![]() $n = m = \pm 1$
, then either r is primitive or
$n = m = \pm 1$
, then either r is primitive or
![]() $H\cong \mathbb {Z}^2$
. If
$H\cong \mathbb {Z}^2$
. If
![]() $n = m\neq \pm 1$
, then H has nontrivial center generated by
$n = m\neq \pm 1$
, then H has nontrivial center generated by
![]() $c^n$
. So, if
$c^n$
. So, if
![]() $n = m$
, we have obtained conclusion (1) or (2). Now suppose that
$n = m$
, we have obtained conclusion (1) or (2). Now suppose that
![]() $n\neq m$
. Therefore, the exponent sum of c in r must be nonzero. There is a single epimorphism, up to sign change,
$n\neq m$
. Therefore, the exponent sum of c in r must be nonzero. There is a single epimorphism, up to sign change,
![]() $\phi :F(a, c)\to \mathbb {Z}$
such that
$\phi :F(a, c)\to \mathbb {Z}$
such that
![]() $\phi (r) = 0$
, given by
$\phi (r) = 0$
, given by
 $$ \begin{align*} a &\to \frac{-\sigma_c(r)}{\gcd(\sigma_a(r), \sigma_c(r))}~,\\ c &\to \frac{\sigma_a(r)}{\gcd(\sigma_a(r), \sigma_c(r))}~, \end{align*} $$
$$ \begin{align*} a &\to \frac{-\sigma_c(r)}{\gcd(\sigma_a(r), \sigma_c(r))}~,\\ c &\to \frac{\sigma_a(r)}{\gcd(\sigma_a(r), \sigma_c(r))}~, \end{align*} $$
where
![]() $\sigma _a(r), \sigma _c(r)$
denote the exponent sums of a and c in r, respectively. But now
$\sigma _a(r), \sigma _c(r)$
denote the exponent sums of a and c in r, respectively. But now
![]() $\phi (a^{-1}c^mac^{-n}) = 0$
from which it follows that
$\phi (a^{-1}c^mac^{-n}) = 0$
from which it follows that
By Magnus rewriting, since
![]() $\sigma _a(r) = 0$
, we have that
$\sigma _a(r) = 0$
, we have that
where
![]() $r'$
is the rewriting of r in terms of
$r'$
is the rewriting of r in terms of
![]() $c = c_0, ..., c_k$
. By the Freiheitssatz (see [Reference Magnus, Karrass and SolitarMKS66, Theorem 4.10]), it follows that
$c = c_0, ..., c_k$
. By the Freiheitssatz (see [Reference Magnus, Karrass and SolitarMKS66, Theorem 4.10]), it follows that
![]() $k = 1$
. If
$k = 1$
. If
![]() $\langle c, aca^{-1}\rangle \cong \mathbb {Z}$
, then we have obtained conclusion (3). If not, then we have obtained conclusion (4).
$\langle c, aca^{-1}\rangle \cong \mathbb {Z}$
, then we have obtained conclusion (3). If not, then we have obtained conclusion (4).
Recall that a generalized Baumslag–Solitar group is group that splits as a graph of groups where each vertex and edge group is infinite cyclic.
Proposition 3.16 Let
![]() $G = \langle a, c \mid r\rangle $
be a one-relator group in which either
$G = \langle a, c \mid r\rangle $
be a one-relator group in which either
![]() $a^m = c^n$
or
$a^m = c^n$
or
![]() $ac^ma^{-1} = c^n$
holds. Then G is a generalized Baumslag–Solitar group.
$ac^ma^{-1} = c^n$
holds. Then G is a generalized Baumslag–Solitar group.
Proof The first case follows from Lemma 3.14 and [Reference PietrowskiPie74, Theorems 1 and 3]. Similarly, in the second case, we may conclude that G is a generalized Baumslag–Solitar group by Lemma 3.15, unless
![]() $n\neq m$
and r or
$n\neq m$
and r or
![]() $r^{-1}$
is conjugate in
$r^{-1}$
is conjugate in
![]() $F(a, c)$
to an element
$F(a, c)$
to an element
![]() $w\in \langle c, a^{-1}ca\rangle $
such that
$w\in \langle c, a^{-1}ca\rangle $
such that
![]() $H = \langle c, a^{-1}ca\rangle \cong F(c, a^{-1}ca)/\langle \langle w \rangle \rangle $
is noncyclic with nontrivial center. So let us suppose that we are in the latter case. Since
$H = \langle c, a^{-1}ca\rangle \cong F(c, a^{-1}ca)/\langle \langle w \rangle \rangle $
is noncyclic with nontrivial center. So let us suppose that we are in the latter case. Since
![]() $ac^ma^{-1} = c^n$
holds in H, the rank of the abelianization of H must be one. Then, by [Reference PietrowskiPie74, Theorem 1], we have
$ac^ma^{-1} = c^n$
holds in H, the rank of the abelianization of H must be one. Then, by [Reference PietrowskiPie74, Theorem 1], we have
where
![]() $p_i, q_i\geq 2$
and
$p_i, q_i\geq 2$
and
![]() $\gcd (p_i, q_j) = 1$
for all
$\gcd (p_i, q_j) = 1$
for all
![]() $i>j$
. Then, by [Reference PietrowskiPie74, Lemma 3], c and
$i>j$
. Then, by [Reference PietrowskiPie74, Lemma 3], c and
![]() $a^{-1}ca$
are both conjugate within H to some subgroup
$a^{-1}ca$
are both conjugate within H to some subgroup
![]() $\langle a_i\rangle <H$
. Suppose that
$\langle a_i\rangle <H$
. Suppose that
![]() $c^g = a_i^k$
and
$c^g = a_i^k$
and
![]() $(a^{-1}ca)^h = a_j^l$
. Then we have that
$(a^{-1}ca)^h = a_j^l$
. Then we have that
where
![]() $b = g^{-1}ah$
. Thus, we may conclude that G is a generalized Baumslag–Solitar group.
$b = g^{-1}ah$
. Thus, we may conclude that G is a generalized Baumslag–Solitar group.
We are now ready to prove the main result of this section.
Theorem 3.17 Let G be an exceptional intersection group. Then one of the following holds:
-
(1) G is a primitive exceptional intersection group and so is
 $2$
-free.
$2$
-free. -
(2) There is a two-generator one-relator generalized Baumslag–Solitar subgroup
 $H<G$
such that every nonfree two-generator subgroup of G is conjugate into H.
$H<G$
such that every nonfree two-generator subgroup of G is conjugate into H.
Proof Assume that G is not a primitive exceptional intersection group. Let
![]() $H<G \cong F(A, B, C)/\langle \langle w \rangle \rangle $
be the two-generator subgroup from Theorem 3.9. We may assume that H is maximal in the sense that there is no subgroup properly containing H and that is of the same form as the two-generator subgroup from Theorem 3.9. By Proposition 3.16, H is a generalized Baumslag–Solitar group. Clearly, H has rank at most two, so we now consider the two possible cases.
$H<G \cong F(A, B, C)/\langle \langle w \rangle \rangle $
be the two-generator subgroup from Theorem 3.9. We may assume that H is maximal in the sense that there is no subgroup properly containing H and that is of the same form as the two-generator subgroup from Theorem 3.9. By Proposition 3.16, H is a generalized Baumslag–Solitar group. Clearly, H has rank at most two, so we now consider the two possible cases.
Let us first assume that H has rank one. Thus, G has one of the following presentations:
-
(1)
 $G \cong \langle \Sigma \mid \operatorname {\mathrm {pr}}_{p/q}(x, y)\rangle $
for some
$G \cong \langle \Sigma \mid \operatorname {\mathrm {pr}}_{p/q}(x, y)\rangle $
for some
 $x\in \langle A, B\rangle - \langle B\rangle $
and
$x\in \langle A, B\rangle - \langle B\rangle $
and
 $y\in \langle B, C\rangle - \langle B\rangle $
,
$y\in \langle B, C\rangle - \langle B\rangle $
, -
(2)
 $G\cong \langle \Sigma \mid \operatorname {\mathrm {pr}}_{p/q}(xy, z)\rangle $
for some
$G\cong \langle \Sigma \mid \operatorname {\mathrm {pr}}_{p/q}(xy, z)\rangle $
for some
 $x\in \langle A, B\rangle - \langle B\rangle $
,
$x\in \langle A, B\rangle - \langle B\rangle $
,
 $y\in \langle B, C\rangle - \langle B\rangle $
and
$y\in \langle B, C\rangle - \langle B\rangle $
and
 $z\in \langle B\rangle $
,
$z\in \langle B\rangle $
,
where
![]() $H = \langle x, y\rangle $
in the first case and
$H = \langle x, y\rangle $
in the first case and
![]() $H = \langle xy, z\rangle $
in the second case.
$H = \langle xy, z\rangle $
in the second case.
Suppose that we are in the first situation. By Definition 3.2, we may assume that either
![]() $\{\langle x\rangle , \langle y\rangle \}$
is not a malnormal family (in
$\{\langle x\rangle , \langle y\rangle \}$
is not a malnormal family (in
![]() $F(A, B, C)$
), or that
$F(A, B, C)$
), or that
![]() $p/q = 1$
and that there exist elements
$p/q = 1$
and that there exist elements
![]() $a\in \langle A, B\rangle - \langle B\rangle $
and
$a\in \langle A, B\rangle - \langle B\rangle $
and
![]() $c\in \langle B, C\rangle - \langle B\rangle $
such that
$c\in \langle B, C\rangle - \langle B\rangle $
such that
![]() $\operatorname {\mathrm {pr}}_1(x, y) = \operatorname {\mathrm {pr}}_1(a, c)$
and
$\operatorname {\mathrm {pr}}_1(x, y) = \operatorname {\mathrm {pr}}_1(a, c)$
and
![]() $\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family (in
$\{\langle a\rangle , \langle c\rangle \}$
is not a malnormal family (in
![]() $F(A, B, C)$
). As the two cases are identical, it suffices to assume that
$F(A, B, C)$
). As the two cases are identical, it suffices to assume that
![]() $\{\langle x\rangle , \langle y\rangle \}$
is not a malnormal family. Now, if
$\{\langle x\rangle , \langle y\rangle \}$
is not a malnormal family. Now, if
![]() $\{\langle x\rangle , \langle y\rangle \}$
is not a malnormal family, then either x is a proper power, y is a proper power, or a conjugate of
$\{\langle x\rangle , \langle y\rangle \}$
is not a malnormal family, then either x is a proper power, y is a proper power, or a conjugate of
![]() $\langle x\rangle $
intersects
$\langle x\rangle $
intersects
![]() $\langle y\rangle $
nontrivially. If either x or y is a proper power, by adjoining a root of x or y to H, we obtain a contradiction to maximality of H. If
$\langle y\rangle $
nontrivially. If either x or y is a proper power, by adjoining a root of x or y to H, we obtain a contradiction to maximality of H. If
![]() $\langle x\rangle ^f\cap \langle y\rangle \neq 1$
for some
$\langle x\rangle ^f\cap \langle y\rangle \neq 1$
for some
![]() $f\in F(\Sigma )$
, it follows that there must be elements
$f\in F(\Sigma )$
, it follows that there must be elements
![]() $g\in \langle A, B\rangle - \langle B\rangle $
,
$g\in \langle A, B\rangle - \langle B\rangle $
,
![]() $h\in \langle B, C\rangle -\langle B\rangle $
, and
$h\in \langle B, C\rangle -\langle B\rangle $
, and
![]() $d\in \langle B\rangle $
such that
$d\in \langle B\rangle $
such that
![]() $\langle x\rangle ^g\cap \langle y\rangle ^{h^{-1}} < \langle d\rangle <\langle B\rangle $
. Now H would be properly contained in
$\langle x\rangle ^g\cap \langle y\rangle ^{h^{-1}} < \langle d\rangle <\langle B\rangle $
. Now H would be properly contained in
![]() $\langle gh, h^{-1}dh\rangle $
. However, since
$\langle gh, h^{-1}dh\rangle $
. However, since
![]() $(gh)(h^{-1}dh)^n(gh)^{-1} = (h^{-1}dh)^m$
holds for some
$(gh)(h^{-1}dh)^n(gh)^{-1} = (h^{-1}dh)^m$
holds for some
![]() $m, n\neq 0$
, we obtain a contradiction to maximality of H again.
$m, n\neq 0$
, we obtain a contradiction to maximality of H again.
Now suppose that we are in the second situation. As before, we may assume that
![]() $\langle z\rangle $
is not malnormal by Definition 3.2. Then z is a proper power and we contradict maximality of H once again.
$\langle z\rangle $
is not malnormal by Definition 3.2. Then z is a proper power and we contradict maximality of H once again.
We may conclude from the above that H must have rank two. Since H cannot be free, we have that
![]() $\pi (w) = 2$
and G has a two-generator w-subgroup K into which H is conjugate by [Reference Louder and WiltonLW22, Corollary 1.10]. If
$\pi (w) = 2$
and G has a two-generator w-subgroup K into which H is conjugate by [Reference Louder and WiltonLW22, Corollary 1.10]. If
![]() $H\neq K$
, we get a contradiction to maximality of H by the definition of w-subgroups and Lemmas 2.3 and 2.4. Thus, (2) holds by [Reference Louder and WiltonLW22, Corollary 1.10].
$H\neq K$
, we get a contradiction to maximality of H by the definition of w-subgroups and Lemmas 2.3 and 2.4. Thus, (2) holds by [Reference Louder and WiltonLW22, Corollary 1.10].
It follows from [Reference LintonLin22a, Theorem 8.2] and Theorem 3.17 that an exceptional intersection group is hyperbolic if and only if it contains no Baumslag–Solitar subgroup. Note that this can also be derived using Corollaries 3.10 and 3.11 and the combination theorem [Reference Bestvina and FeighnBF92]. However, in order to prove our main results, we need the stronger dichotomy established in Theorem 3.17. This dichotomy is harder to establish using Corollaries 3.10 and 3.11 as the splittings do not satisfy the hypothesis of existing
![]() $2$
-free combination theorems (see [Reference BaumslagBau68] for example).
$2$
-free combination theorems (see [Reference BaumslagBau68] for example).
Example 3.19 We give two examples of groups with exceptional intersection that are not
![]() $2$
-free. Let
$2$
-free. Let
![]() $p/q\in \mathbb {Q}_{>0}$
and
$p/q\in \mathbb {Q}_{>0}$
and
![]() $n, m\neq 0$
. Consider the group with presentation
$n, m\neq 0$
. Consider the group with presentation
The relation
![]() $c_0^{qm} = c_1^{pn}$
holds in G and so it has an exceptional intersection of the first type. In [Reference Meskin, Pietrowski and SteinbergMPS73], this group was shown to be isomorphic to a noncyclic generalized Baumslag–Solitar group with presentation
$c_0^{qm} = c_1^{pn}$
holds in G and so it has an exceptional intersection of the first type. In [Reference Meskin, Pietrowski and SteinbergMPS73], this group was shown to be isomorphic to a noncyclic generalized Baumslag–Solitar group with presentation
and so is not
![]() $2$
-free.
$2$
-free.
Now consider the HNN-extension
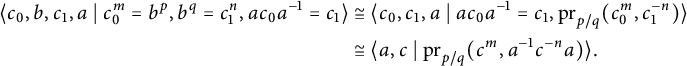 $$ \begin{align*} \langle c_0, b, c_1 , a\mid c_0^{m} = b^{p}, b^{q} = c_1^{n}, ac_0a^{-1} = c_1\rangle &\cong \langle c_0, c_1, a \mid ac_0a^{-1} = c_1, \operatorname{\mathrm{pr}}_{p/q}(c_0^m, c_1^{-n}) \rangle \\ &\cong \langle a, c \mid \operatorname{\mathrm{pr}}_{p/q}(c^m, a^{-1}c^{-n}a)\rangle. \end{align*} $$
$$ \begin{align*} \langle c_0, b, c_1 , a\mid c_0^{m} = b^{p}, b^{q} = c_1^{n}, ac_0a^{-1} = c_1\rangle &\cong \langle c_0, c_1, a \mid ac_0a^{-1} = c_1, \operatorname{\mathrm{pr}}_{p/q}(c_0^m, c_1^{-n}) \rangle \\ &\cong \langle a, c \mid \operatorname{\mathrm{pr}}_{p/q}(c^m, a^{-1}c^{-n}a)\rangle. \end{align*} $$
The relation
![]() $a^{-1}c^{mp}a = c^{nq}$
holds in this group and so
$a^{-1}c^{mp}a = c^{nq}$
holds in this group and so
has an exceptional intersection of the second type. This group also contains a noncyclic generalized Baumslag–Solitar subgroup and so is not
![]() $2$
-free.
$2$
-free.
4 One-relator towers
A one-relator complex is a combinatorial
![]() $2$
-complex with a single
$2$
-complex with a single
![]() $2$
-cell. If X is a one-relator complex, we write
$2$
-cell. If X is a one-relator complex, we write
![]() $X = (\Gamma , \lambda )$
where
$X = (\Gamma , \lambda )$
where
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $1$
-complex and
$1$
-complex and
![]() $\lambda :S^1\looparrowright \Gamma $
is the attaching map. In this section, we are going to use and generalize some of the results from [Reference LintonLin22a, Reference LintonLin22b].
$\lambda :S^1\looparrowright \Gamma $
is the attaching map. In this section, we are going to use and generalize some of the results from [Reference LintonLin22a, Reference LintonLin22b].
If
![]() $p:Y\looparrowright X$
is an infinite cyclic cover of a CW-complex, a tree domain for p is a subcomplex
$p:Y\looparrowright X$
is an infinite cyclic cover of a CW-complex, a tree domain for p is a subcomplex
![]() $Z\subset Y$
satisfying the following:
$Z\subset Y$
satisfying the following:
-
(1)
 $\mathbb {Z}\cdot Z = Y$
.
$\mathbb {Z}\cdot Z = Y$
. -
(2) For all
 $k\in \mathbb {N}$
and every cell
$k\in \mathbb {N}$
and every cell
 $c\subset Z$
, if
$c\subset Z$
, if
 $k\cdot c\subset Z$
, then
$k\cdot c\subset Z$
, then
 $i\cdot c\subset Z$
for all
$i\cdot c\subset Z$
for all
 $0\leq i\leq k$
.
$0\leq i\leq k$
. -
(3)
 $Z\cap 1\cdot Z$
is connected and nonempty.
$Z\cap 1\cdot Z$
is connected and nonempty.
By [Reference LintonLin22a, Proposition 3.10], if the map
![]() $\pi _1(Z\cap 1\cdot Z)\to \pi _1(Z)$
induced by inclusion is injective, then we obtain a splitting
$\pi _1(Z\cap 1\cdot Z)\to \pi _1(Z)$
induced by inclusion is injective, then we obtain a splitting
By [Reference LintonLin22a, Proposition 4.7], if
![]() $p:Y\looparrowright X$
is an infinite cyclic cover of a one-relator complex, then there always exists a one-relator tree domain Z for p. Moreover, by the Freiheitssatz, the maps
$p:Y\looparrowright X$
is an infinite cyclic cover of a one-relator complex, then there always exists a one-relator tree domain Z for p. Moreover, by the Freiheitssatz, the maps
![]() $\pi _1(Z\cap 1\cdot Z)\to \pi _1(Z)$
are always injective.
$\pi _1(Z\cap 1\cdot Z)\to \pi _1(Z)$
are always injective.
A one-relator tower is a sequence of immersions of one-relator complexes
where
![]() $X_{i+1}\looparrowright X_i$
factors as
$X_{i+1}\looparrowright X_i$
factors as
where p is an infinite cyclic covering map and
![]() $\iota $
is an inclusion of a tree domain for p. A one-relator tower is maximal if
$\iota $
is an inclusion of a tree domain for p. A one-relator tower is maximal if
![]() $\chi (X_N) = 1$
.
$\chi (X_N) = 1$
.
By the above, it follows that one-relator hierarchies correspond to iterated HNN-extensions over one-relator groups.
The following is [Reference LintonLin22a, Proposition 5.1] and can be interpreted as a modern version of the well-known Magnus–Moldavanskii hierarchy.
Proposition 4.1 Let X be a finite one-relator complex. Then X has a maximal one-relator tower.
If
![]() $X = (\Gamma , \lambda )$
is a one-relator complex, then for each w-subgroup
$X = (\Gamma , \lambda )$
is a one-relator complex, then for each w-subgroup
![]() $K<\pi _1(\Gamma )$
, where
$K<\pi _1(\Gamma )$
, where
![]() $w = [\lambda ]$
, there is an immersion of one-relator complexes
$w = [\lambda ]$
, there is an immersion of one-relator complexes
![]() $Q = (\Omega , \omega )\looparrowright X$
where
$Q = (\Omega , \omega )\looparrowright X$
where
![]() $\Omega \looparrowright \Gamma $
is the core graph immersion representing K. We say that
$\Omega \looparrowright \Gamma $
is the core graph immersion representing K. We say that
![]() $Q\looparrowright X$
represents a w-subgroup. The following is [Reference LintonLin22a, Theorem 5.15].
$Q\looparrowright X$
represents a w-subgroup. The following is [Reference LintonLin22a, Theorem 5.15].
Theorem 4.2 Let X be a one-relator complex, and let
![]() $Q\looparrowright X$
be an immersion of a one-relator complex, representing some w-subgroup. There exists a one-relator tower
$Q\looparrowright X$
be an immersion of a one-relator complex, representing some w-subgroup. There exists a one-relator tower
Equipped with Theorem 4.2, we make the following definition.
Definition 4.1 We say a one-relator tower
![]() $X_N\looparrowright \cdots \looparrowright X_0 = X$
is factored if for every immersion
$X_N\looparrowright \cdots \looparrowright X_0 = X$
is factored if for every immersion
![]() $Q\looparrowright X_i$
representing a w-subgroup of
$Q\looparrowright X_i$
representing a w-subgroup of
![]() $\pi _1(X_i)$
with
$\pi _1(X_i)$
with
![]() $\chi (Q) = 0$
, either there is some
$\chi (Q) = 0$
, either there is some
![]() $j\geq 0$
such that
$j\geq 0$
such that
![]() $X_{i+j} = Q\looparrowright X_i$
, or
$X_{i+j} = Q\looparrowright X_i$
, or
![]() $Q\looparrowright X_i$
factors through
$Q\looparrowright X_i$
factors through
![]() $X_N\looparrowright X_i$
.
$X_N\looparrowright X_i$
.
The proof of the following is essentially identical to that of Proposition 4.1, but we include it for completeness.
Proposition 4.3 Every one-relator complex has a maximal factored one-relator tower.
Proof Let
![]() $X = (\Gamma , \lambda )$
be a one-relator complex. Denote by
$X = (\Gamma , \lambda )$
be a one-relator complex. Denote by
![]() $\deg (\lambda )$
the largest degree covering map
$\deg (\lambda )$
the largest degree covering map
![]() $S^1\looparrowright S^1$
that
$S^1\looparrowright S^1$
that
![]() $\lambda $
factors through and denote by
$\lambda $
factors through and denote by
![]() $X_{\lambda }$
the smallest one-relator subcomplex of X. Then define the quantity
$X_{\lambda }$
the smallest one-relator subcomplex of X. Then define the quantity
 $$\begin{align*}c(X) = \left(\frac{{\lvert {\lambda} \rvert}}{\deg(\lambda)} - {\lvert {X_{\lambda}^{(0)}} \rvert}, -\chi(X)\right). \end{align*}$$
$$\begin{align*}c(X) = \left(\frac{{\lvert {\lambda} \rvert}}{\deg(\lambda)} - {\lvert {X_{\lambda}^{(0)}} \rvert}, -\chi(X)\right). \end{align*}$$
The proof proceeds by induction on
![]() $c(X)$
.
$c(X)$
.
If
![]() $\pi _1(X)$
is
$\pi _1(X)$
is
![]() $2$
-free or has torsion, then any maximal one-relator tower is a factored tower by definition and so the result follows from Proposition 4.1. If
$2$
-free or has torsion, then any maximal one-relator tower is a factored tower by definition and so the result follows from Proposition 4.1. If
![]() $Q\looparrowright X$
represents a w-subgroup, then it is clear that we must have
$Q\looparrowright X$
represents a w-subgroup, then it is clear that we must have
![]() $c(Q)\leq c(X)$
with equality if and only if
$c(Q)\leq c(X)$
with equality if and only if
![]() $Q = X$
. Thus, by Theorem 4.2, we may assume that
$Q = X$
. Thus, by Theorem 4.2, we may assume that
![]() $\chi (X) = 0$
. Then as
$\chi (X) = 0$
. Then as
![]() $\chi (X)\neq 1$
,
$\chi (X)\neq 1$
,
![]() $\pi _1(X)$
is indicable and there is some infinite cyclic cover
$\pi _1(X)$
is indicable and there is some infinite cyclic cover
![]() $p:Y\looparrowright X$
. By [Reference LintonLin22a, Proposition 4.9], there is some one-relator tree domain Z for p such that
$p:Y\looparrowright X$
. By [Reference LintonLin22a, Proposition 4.9], there is some one-relator tree domain Z for p such that
![]() $c(Z)<c(X)$
. Hence, by induction, the proof is complete.
$c(Z)<c(X)$
. Hence, by induction, the proof is complete.
4.1 Acylindrical, quasi-convex, and stable one-relator towers
Let
![]() $X_K\looparrowright \cdots \looparrowright X_1\looparrowright X_0$
be a one-relator tower. Denote by
$X_K\looparrowright \cdots \looparrowright X_1\looparrowright X_0$
be a one-relator tower. Denote by
![]() $T_i$
the Bass–Serre tree associated with the splitting
$T_i$
the Bass–Serre tree associated with the splitting
![]() $\pi _1(X_i) \cong \pi _1(X_{i+1})*_{\psi _i}$
. We call this an acylindrical one-relator tower if there is some constant
$\pi _1(X_i) \cong \pi _1(X_{i+1})*_{\psi _i}$
. We call this an acylindrical one-relator tower if there is some constant
![]() $k\geq 0$
such that the stabilizers of segments of length k in
$k\geq 0$
such that the stabilizers of segments of length k in
![]() $T_i$
are finite. We call it a quasi-convex one-relator tower if the inclusions
$T_i$
are finite. We call it a quasi-convex one-relator tower if the inclusions
![]() $\tilde {A}_{i+1}, \tilde {B}_{i+1}\hookrightarrow \tilde {X_i}$
are quasi-isometric embeddings, where
$\tilde {A}_{i+1}, \tilde {B}_{i+1}\hookrightarrow \tilde {X_i}$
are quasi-isometric embeddings, where
![]() $A_{i+1} = X_{i+1}\cap 1\cdot X_{i+1}$
and
$A_{i+1} = X_{i+1}\cap 1\cdot X_{i+1}$
and
![]() $B_{i+1} = -1\cdot X_{i+1}\cap X_{i+1}$
. This last definition is due to Wise [Reference WiseWis21], adapted to the one-relator case. In [Reference LintonLin22a], a stable one-relator tower is defined in terms of the identifying homomorphisms
$B_{i+1} = -1\cdot X_{i+1}\cap X_{i+1}$
. This last definition is due to Wise [Reference WiseWis21], adapted to the one-relator case. In [Reference LintonLin22a], a stable one-relator tower is defined in terms of the identifying homomorphisms
![]() $\psi _i$
. Since we shall not need this definition, we instead record the following, which is a reformulation of [Reference LintonLin22a, Lemma 7.4].
$\psi _i$
. Since we shall not need this definition, we instead record the following, which is a reformulation of [Reference LintonLin22a, Lemma 7.4].
Lemma 4.4 A one-relator tower
![]() $X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0$
is stable if and only if there is some
$X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0$
is stable if and only if there is some
![]() $k\geq 0$
such that the pointwise stabilisers of segments of length k in
$k\geq 0$
such that the pointwise stabilisers of segments of length k in
![]() $T_i$
have rank at most one.
$T_i$
have rank at most one.
In [Reference LintonLin22a], the author established a connection between these three types of one-relator towers. The aim of this section is to improve on that result.
4.2 Primitive extension complexes
A one-relator complex X is a primitive extension complex if
![]() $\chi (X) = 0$
and there is a one-relator tower
$\chi (X) = 0$
and there is a one-relator tower
![]() $Z\looparrowright X$
where
$Z\looparrowright X$
where
![]() $\pi _1(Z)$
is
$\pi _1(Z)$
is
![]() $2$
-free and such that
$2$
-free and such that
after possibly adding edges to Z and extending the
![]() $\mathbb {Z}$
-action so that
$\mathbb {Z}$
-action so that
![]() $-1\cdot Z\cap Z\cap 1\cdot Z$
is connected. By Theorem 3.17, we can see that
$-1\cdot Z\cap Z\cap 1\cdot Z$
is connected. By Theorem 3.17, we can see that
![]() $\pi _1(Z)*F$
is a primitive exceptional intersection group for some finitely generated free group F.
$\pi _1(Z)*F$
is a primitive exceptional intersection group for some finitely generated free group F.
Let
![]() $X = (\Gamma , \lambda )$
be a one-relator complex with
$X = (\Gamma , \lambda )$
be a one-relator complex with
![]() $\chi (X) = 0$
. Let
$\chi (X) = 0$
. Let
![]() $T\subset \Gamma $
be a spanning tree, and let
$T\subset \Gamma $
be a spanning tree, and let
![]() $\langle a, b \mid w\rangle $
be the induced one-relator presentation. If
$\langle a, b \mid w\rangle $
be the induced one-relator presentation. If
![]() $a^m = b^n$
for some
$a^m = b^n$
for some
![]() $m, n\in \mathbb {Z}-\{0\}$
and
$m, n\in \mathbb {Z}-\{0\}$
and
![]() $\pi _1(X)$
is not cyclic, then we call X a powered one-relator complex. By Proposition 3.16,
$\pi _1(X)$
is not cyclic, then we call X a powered one-relator complex. By Proposition 3.16,
![]() $\pi _1(X)$
is a generalized Baumslag–Solitar group. Moreover, we have the following.
$\pi _1(X)$
is a generalized Baumslag–Solitar group. Moreover, we have the following.
Lemma 4.5 Powered one-relator complexes are primitive extension complexes.
Proof Let
![]() $X = (\Gamma , \lambda )$
be a powered one-relator complex. Then there is a spanning tree in
$X = (\Gamma , \lambda )$
be a powered one-relator complex. Then there is a spanning tree in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $a^m = b^n$
where
$a^m = b^n$
where
![]() $\langle a, b\mid w\rangle $
is the induced presentation for
$\langle a, b\mid w\rangle $
is the induced presentation for
![]() $\pi _1(X)$
. By virtue of the fact that
$\pi _1(X)$
. By virtue of the fact that
![]() $a^m = b^n$
, there is only a single epimorphism
$a^m = b^n$
, there is only a single epimorphism
![]() $\phi :\pi _1(X)\to \mathbb {Z}$
and by [Reference MurasugiMur64], we have that
$\phi :\pi _1(X)\to \mathbb {Z}$
and by [Reference MurasugiMur64], we have that
![]() $\ker (\phi )$
is finitely generated and free. Now let
$\ker (\phi )$
is finitely generated and free. Now let
![]() $p:Y\looparrowright X$
be the induced cyclic cover and
$p:Y\looparrowright X$
be the induced cyclic cover and
![]() $Z\subset Y$
a one-relator tree domain. Since
$Z\subset Y$
a one-relator tree domain. Since
![]() $\pi _1(Y)$
is finitely generated, this in particular implies that
$\pi _1(Y)$
is finitely generated, this in particular implies that
and so that X is a primitive extension complex.
It turns out that primitive extension complexes obstruct stable one-relator towers.
Proposition 4.6 Let X be a one-relator complex and
![]() $X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
a factored one-relator tower. Then one of the following holds:
$X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
a factored one-relator tower. Then one of the following holds:
-
(1)
 $X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is stable.
$X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is stable. -
(2)
 $X_K\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is stable, and
$X_K\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is stable, and
 $X_K$
is a primitive extension complex for some
$X_K$
is a primitive extension complex for some
 $K\leq N$
.
$K\leq N$
. -
(3)
 $X_K$
is a powered one-relator complex for some
$X_K$
is a powered one-relator complex for some
 $K\leq N$
.
$K\leq N$
.
Proof Let
![]() $p:Y\looparrowright X$
be the cyclic cover such that
$p:Y\looparrowright X$
be the cyclic cover such that
![]() $X_1$
is a tree domain for p. Let
$X_1$
is a tree domain for p. Let
![]() $A = X_1\cap -1\cdot X_1$
and
$A = X_1\cap -1\cdot X_1$
and
![]() $B = X_1\cap 1\cdot X_1$
, where the
$B = X_1\cap 1\cdot X_1$
, where the
![]() $\mathbb {Z}$
action is the covering action. Up to possibly adding finitely many edges to X (and so to
$\mathbb {Z}$
action is the covering action. Up to possibly adding finitely many edges to X (and so to
![]() $X_1$
), we may assume that
$X_1$
), we may assume that
![]() $A\cap B$
is connected. Now, by [Reference LintonLin22a, Lemma 7.8], either
$A\cap B$
is connected. Now, by [Reference LintonLin22a, Lemma 7.8], either
![]() $X_1\looparrowright X_0 = X$
is stable, or
$X_1\looparrowright X_0 = X$
is stable, or
![]() $\pi _1(A)\cap \pi _1(B)\neq \pi _1(A\cap B)$
. If
$\pi _1(A)\cap \pi _1(B)\neq \pi _1(A\cap B)$
. If
![]() $X_1\looparrowright X_0$
is stable, we proceed by induction. So suppose that it is not. By Theorem 3.1, either
$X_1\looparrowright X_0$
is stable, we proceed by induction. So suppose that it is not. By Theorem 3.1, either
![]() $\pi _1(X_1)$
is
$\pi _1(X_1)$
is
![]() $2$
-free, or there is an immersion
$2$
-free, or there is an immersion
![]() $Q\looparrowright X_1$
representing a w-subgroup such that
$Q\looparrowright X_1$
representing a w-subgroup such that
![]() $\chi (Q) = 0$
and
$\chi (Q) = 0$
and
![]() $\pi _1(Q)$
is a generalized Baumslag–Solitar group. Let us first consider the latter case. By definition of factored one-relator towers, there is some i such that
$\pi _1(Q)$
is a generalized Baumslag–Solitar group. Let us first consider the latter case. By definition of factored one-relator towers, there is some i such that
![]() $X_i = Q$
. Moreover, by Lemmas 3.14 and 3.15, either
$X_i = Q$
. Moreover, by Lemmas 3.14 and 3.15, either
![]() $X_i$
is a powered one-relator complex, or
$X_i$
is a powered one-relator complex, or
![]() $X_{i+1}$
is. So now let us consider the case that
$X_{i+1}$
is. So now let us consider the case that
![]() $\pi _1(X_1)$
is
$\pi _1(X_1)$
is
![]() $2$
-free. If
$2$
-free. If
![]() $\chi (X)<0$
, then by definition, we have that X is
$\chi (X)<0$
, then by definition, we have that X is
![]() $2$
-free. Thus, by [Reference LintonLin22a, Theorems 7.8 and 7.9], we have that
$2$
-free. Thus, by [Reference LintonLin22a, Theorems 7.8 and 7.9], we have that
![]() $X_N\looparrowright \cdots \looparrowright X_0 = X$
is a stable tower. If
$X_N\looparrowright \cdots \looparrowright X_0 = X$
is a stable tower. If
![]() $\chi (X) = 0$
, then X is a primitive extension complex.
$\chi (X) = 0$
, then X is a primitive extension complex.
4.3 Improved one-relator towers
Recall that a Magnus subgroup of a one-relator group
![]() $\langle \Sigma \mid w\rangle $
is a subgroup generated by a subset of the generators
$\langle \Sigma \mid w\rangle $
is a subgroup generated by a subset of the generators
![]() $A\subset \Sigma $
such that A omits a generator that appears in the cyclic reduction of w. Using Proposition 4.6, we may now prove that Magnus subgroups of hyperbolic one-relator groups are quasi-convex. This was previously known in the case of one-relator groups with torsion by Newman’s spelling theorem and in the case of
$A\subset \Sigma $
such that A omits a generator that appears in the cyclic reduction of w. Using Proposition 4.6, we may now prove that Magnus subgroups of hyperbolic one-relator groups are quasi-convex. This was previously known in the case of one-relator groups with torsion by Newman’s spelling theorem and in the case of
![]() $2$
-free one-relator groups by [Reference LintonLin22a, Theorems 8.1 and 8.2].
$2$
-free one-relator groups by [Reference LintonLin22a, Theorems 8.1 and 8.2].
Theorem 4.7 Magnus subgroups of hyperbolic one-relator groups are quasi-convex.
Proof Let X be a one-relator complex with
![]() $\pi _1(X)$
hyperbolic. By Proposition 4.3, there is a maximal factored one-relator tower
$\pi _1(X)$
hyperbolic. By Proposition 4.3, there is a maximal factored one-relator tower
![]() $X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
. By [Reference GerstenGer96, Corollary 7.8],
$X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
. By [Reference GerstenGer96, Corollary 7.8],
![]() $\pi _1(X_i)$
is hyperbolic for all
$\pi _1(X_i)$
is hyperbolic for all
![]() $i\geq 1$
. By Proposition 4.6, either this tower is stable, or there is some
$i\geq 1$
. By Proposition 4.6, either this tower is stable, or there is some
![]() $1\leq L<N$
such that
$1\leq L<N$
such that
![]() $X_L\looparrowright \cdots \looparrowright X_1$
is stable and
$X_L\looparrowright \cdots \looparrowright X_1$
is stable and
![]() $X_L$
is a primitive extension complex.
$X_L$
is a primitive extension complex.
In the first case, since hyperbolic groups cannot contain Baumslag–Solitar subgroups, the result follows by [Reference LintonLin22a, Theorems 8.1 and 8.2]. So now let us assume that we are in the second case. The proof proceeds by induction on tower length. For the base case
![]() $L=1$
, since
$L=1$
, since
![]() $\chi (X_L) = 0$
, all Magnus subgroups of
$\chi (X_L) = 0$
, all Magnus subgroups of
![]() $\pi _1(X_L)$
must by quasi-convex as they are all cyclic. So now we assume the inductive hypothesis. In other words, that all Magnus subgroups of
$\pi _1(X_L)$
must by quasi-convex as they are all cyclic. So now we assume the inductive hypothesis. In other words, that all Magnus subgroups of
![]() $\pi _1(X_1)$
are quasi-convex. Then by [Reference LintonLin22a, Theorems 3.6 and 6.10], all Magnus subgroups of
$\pi _1(X_1)$
are quasi-convex. Then by [Reference LintonLin22a, Theorems 3.6 and 6.10], all Magnus subgroups of
![]() $\pi _1(X)$
are quasi-convex and the proof is complete.
$\pi _1(X)$
are quasi-convex and the proof is complete.
As a consequence, we may improve on the main tool developed in [Reference LintonLin22a].
Theorem 4.8 Let X be a one-relator complex, and let
![]() $Z\looparrowright X$
be a one-relator tower. If
$Z\looparrowright X$
be a one-relator tower. If
![]() $\pi _1(Z)$
is hyperbolic (and virtually special), then the following are equivalent:
$\pi _1(Z)$
is hyperbolic (and virtually special), then the following are equivalent:
-
(1)
 $Z\looparrowright X$
is a quasi-convex tower and
$Z\looparrowright X$
is a quasi-convex tower and
 $\pi _1(X)$
is hyperbolic (and virtually special).
$\pi _1(X)$
is hyperbolic (and virtually special). -
(2)
 $Z\looparrowright X$
is an acylindrical tower.
$Z\looparrowright X$
is an acylindrical tower. -
(3)
 $Z\looparrowright X$
is a stable tower and
$Z\looparrowright X$
is a stable tower and
 $\pi _1(X)$
contains no Baumslag–Solitar subgroups.
$\pi _1(X)$
contains no Baumslag–Solitar subgroups.
Moreover, if any of the above is satisfied, then
![]() $\pi _1(Z)<\pi _1(X)$
is quasi-convex.
$\pi _1(Z)<\pi _1(X)$
is quasi-convex.
Proof By Theorem 4.7, Magnus subgroups of
![]() $\pi _1(Z)$
are quasi-convex. By [Reference LintonLin22a, Theorem 7.16] and [Reference WiseWis21, Theorem 13.1], we may establish the equivalence between (2) and (3). Similarly, by [Reference LintonLin22a, Theorem 3.6] and [Reference WiseWis21, Theorem 13.1], we may establish the equivalence between (2) and (1).
$\pi _1(Z)$
are quasi-convex. By [Reference LintonLin22a, Theorem 7.16] and [Reference WiseWis21, Theorem 13.1], we may establish the equivalence between (2) and (3). Similarly, by [Reference LintonLin22a, Theorem 3.6] and [Reference WiseWis21, Theorem 13.1], we may establish the equivalence between (2) and (1).
Combining Proposition 4.6 and Theorem 4.8 and using induction, we obtain the following corollary.
Corollary 4.9 Let X be a one-relator complex and suppose that
![]() $\pi _1(X)$
contains no Baumslag–Solitar subgroups. If
$\pi _1(X)$
contains no Baumslag–Solitar subgroups. If
![]() $X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is a maximal factored one-relator tower, then one of the following holds:
$X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is a maximal factored one-relator tower, then one of the following holds:
-
(1)
 $\pi _1(X)$
is hyperbolic and virtually special and
$\pi _1(X)$
is hyperbolic and virtually special and
 $X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is an acylindrical tower,
$X_N\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is an acylindrical tower, -
(2)
 $X_K$
is a primitive extension complex for some
$X_K$
is a primitive extension complex for some
 $K\geq 0$
and, if
$K\geq 0$
and, if
 $\pi _1(X_K)$
is hyperbolic (and virtually special), then
$\pi _1(X_K)$
is hyperbolic (and virtually special), then
 $\pi _1(X)$
is hyperbolic (and virtually special) and
$\pi _1(X)$
is hyperbolic (and virtually special) and
 $X_K\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is an acylindrical tower.
$X_K\looparrowright \cdots \looparrowright X_1\looparrowright X_0 = X$
is an acylindrical tower.
5 Primitive extension groups
Let
![]() $i<j\in \mathbb {Z}$
and denote by
$i<j\in \mathbb {Z}$
and denote by
where
![]() $a^{t^k}$
denotes
$a^{t^k}$
denotes
![]() $t^{-k}at^k$
. The reader should remind themselves of the definitions of primitive exceptional intersection words from Section 3.1. For each
$t^{-k}at^k$
. The reader should remind themselves of the definitions of primitive exceptional intersection words from Section 3.1. For each
![]() $p/q\in \mathbb {Q}_{>0}$
, we define two new families of one-relator groups. The first family is parametrized by two words
$p/q\in \mathbb {Q}_{>0}$
, we define two new families of one-relator groups. The first family is parametrized by two words
 $$ \begin{align*} x &\in \langle A_{0, k-1}\rangle - \langle A_{1, k-1}\rangle~,\\ y &\in \langle A_{1, k}\rangle - \langle A_{1, k-1}\rangle~ \end{align*} $$
$$ \begin{align*} x &\in \langle A_{0, k-1}\rangle - \langle A_{1, k-1}\rangle~,\\ y &\in \langle A_{1, k}\rangle - \langle A_{1, k-1}\rangle~ \end{align*} $$
such that
![]() $\operatorname {\mathrm {pr}}_{p/q}(x, y)$
is a primitive exceptional intersection word of the first type (as an element of
$\operatorname {\mathrm {pr}}_{p/q}(x, y)$
is a primitive exceptional intersection word of the first type (as an element of
![]() $F(A_{0, k})$
). We then define
$F(A_{0, k})$
). We then define
We call this a primitive extension group of the first type.
The second family is parametrized by three words
 $$ \begin{align*} x &\in \langle A_{0, k-1}\rangle - \langle A_{1, k-1}\rangle~,\\ y &\in \langle A_{1, k}\rangle - \langle A_{1, k-1}\rangle~,\\ z &\in \langle A_{1, k-1}\rangle-1~ \end{align*} $$
$$ \begin{align*} x &\in \langle A_{0, k-1}\rangle - \langle A_{1, k-1}\rangle~,\\ y &\in \langle A_{1, k}\rangle - \langle A_{1, k-1}\rangle~,\\ z &\in \langle A_{1, k-1}\rangle-1~ \end{align*} $$
such that
![]() $\operatorname {\mathrm {pr}}_{p/q}(xy, z)$
is a primitive exceptional intersection word of the second type (as an element of
$\operatorname {\mathrm {pr}}_{p/q}(xy, z)$
is a primitive exceptional intersection word of the second type (as an element of
![]() $F(A_{0, k})$
). We then define
$F(A_{0, k})$
). We then define
We call this a primitive extension group of the second type.
Definition 5.1 A group G is a primitive extension group if G is a primitive extension group of the first type
as in (5.1) or if G is a primitive extension group of the second type
as in (5.2).
It follows from Corollary 3.10 that
![]() $E_{p/q}(x, y)$
has the following graph of groups decomposition:
$E_{p/q}(x, y)$
has the following graph of groups decomposition:

Similarly, it follows from Corollary 3.11 that
![]() $F_{p/q}(x, y, z)$
has the following graph of groups decomposition:
$F_{p/q}(x, y, z)$
has the following graph of groups decomposition:

where H takes the following form:
Note that since
![]() $xy$
is primitive in
$xy$
is primitive in
![]() $F(x, y)$
, we see that
$F(x, y)$
, we see that
If G is a finitely presented group, we denote by
![]() $\delta _G$
its Dehn function. Although the class of one-relator groups containing groups with Dehn function not bounded by any finite tower of exponentials [Reference GerstenGer92a], the Dehn function of primitive extension groups cannot be worse than exponential.
$\delta _G$
its Dehn function. Although the class of one-relator groups containing groups with Dehn function not bounded by any finite tower of exponentials [Reference GerstenGer92a], the Dehn function of primitive extension groups cannot be worse than exponential.
Lemma 5.1 If G is a primitive extension group, then
![]() $\delta _G(n)\preceq \exp (n)$
.
$\delta _G(n)\preceq \exp (n)$
.
Proof Since primitive extension groups split as graphs of hyperbolic groups with finitely generated undistorted edge groups, the upper bound follows from [Reference BernasconiBer94, Theorem 2].
We say two one-relator complexes
![]() $X = (\Gamma , \lambda )$
and
$X = (\Gamma , \lambda )$
and
![]() $Q = (\Delta , \omega )$
are Nielsen equivalent if there is a homotopy equivalence
$Q = (\Delta , \omega )$
are Nielsen equivalent if there is a homotopy equivalence
![]() $f:\Gamma \to \Lambda $
and a homeomorphism
$f:\Gamma \to \Lambda $
and a homeomorphism
![]() $s:S^1\to S^1$
such that
$s:S^1\to S^1$
such that
![]() $f\circ \lambda \simeq \omega \circ s$
. This is a strong version of homotopy equivalence for one-relator complexes, introduced in [Reference Louder and WiltonLW22].
$f\circ \lambda \simeq \omega \circ s$
. This is a strong version of homotopy equivalence for one-relator complexes, introduced in [Reference Louder and WiltonLW22].
Lemma 5.2 If X is a primitive extension complex, then X is Nielsen equivalent to a presentation complex for (5.1) or (5.2).
Proof Denote by
![]() $X = (\Gamma , \lambda )$
. Without loss, we may assume that
$X = (\Gamma , \lambda )$
. Without loss, we may assume that
![]() $\Gamma $
is a rose graph. Denote by a and b the two edges in
$\Gamma $
is a rose graph. Denote by a and b the two edges in
![]() $\Gamma $
. This then yields a one-relator presentation
$\Gamma $
. This then yields a one-relator presentation
![]() $\langle a, b \mid w\rangle $
for
$\langle a, b \mid w\rangle $
for
![]() $\pi _1(X)$
.
$\pi _1(X)$
.
By definition, there is a cyclic cover
![]() $p:Y\looparrowright X$
and a one-relator tree domain
$p:Y\looparrowright X$
and a one-relator tree domain
![]() $Z\subset Y$
such that
$Z\subset Y$
such that
after possibly adding edges to Z and extending the
![]() $\mathbb {Z}$
-action so that
$\mathbb {Z}$
-action so that
![]() $-1\cdot Z\cap Z\cap 1\cdot Z$
is connected.
$-1\cdot Z\cap Z\cap 1\cdot Z$
is connected.
Now the epimorphism
![]() $\pi _1(X)\to \mathbb {Z}$
is induced by an epimorphism
$\pi _1(X)\to \mathbb {Z}$
is induced by an epimorphism
![]() $\pi _1(\Gamma )\to \mathbb {Z}$
. Suppose that a maps to zero and b maps to
$\pi _1(\Gamma )\to \mathbb {Z}$
. Suppose that a maps to zero and b maps to
![]() $\pm 1$
(or vice versa) under this homomorphism. Then we see that
$\pm 1$
(or vice versa) under this homomorphism. Then we see that
![]() $\pi _1(Z)$
is conjugate to
$\pi _1(Z)$
is conjugate to
![]() $\langle a, b^{-1}ab, ..., b^{-k}ab^k\rangle $
for some
$\langle a, b^{-1}ab, ..., b^{-k}ab^k\rangle $
for some
![]() $k\geq 0$
. Moreover, that
$k\geq 0$
. Moreover, that
![]() $-1\cdot Z\cap Z\cap 1\cdot Z$
is connected and that
$-1\cdot Z\cap Z\cap 1\cdot Z$
is connected and that
![]() $\langle a, b\mid w\rangle $
is thus a primitive extension presentation.
$\langle a, b\mid w\rangle $
is thus a primitive extension presentation.
Suppose instead that a maps to p and b maps to
![]() $-q$
under the homomorphism to
$-q$
under the homomorphism to
![]() $\mathbb {Z}$
, with
$\mathbb {Z}$
, with
![]() $p, q>0$
. Let
$p, q>0$
. Let
![]() $X' = (\Gamma ', \lambda ')$
be the one-relator complex where
$X' = (\Gamma ', \lambda ')$
be the one-relator complex where
![]() $\Gamma '$
has two edges, x and y, and
$\Gamma '$
has two edges, x and y, and
![]() $\lambda '$
is pulled back via the homotopy equivalence
$\lambda '$
is pulled back via the homotopy equivalence
![]() $f:\Gamma '\to \Gamma $
defined by mapping x to
$f:\Gamma '\to \Gamma $
defined by mapping x to
![]() $\operatorname {\mathrm {pr}}_{p/q}(a, b)$
and y to
$\operatorname {\mathrm {pr}}_{p/q}(a, b)$
and y to
![]() $\operatorname {\mathrm {pr}}_{c/d}(a, b)$
, where
$\operatorname {\mathrm {pr}}_{c/d}(a, b)$
, where
![]() $c, d$
are integers such that
$c, d$
are integers such that
![]() $cp - dq = 1$
. The two one-relator complexes are Nielsen equivalent by construction. Now the induced epimorphism
$cp - dq = 1$
. The two one-relator complexes are Nielsen equivalent by construction. Now the induced epimorphism
![]() $\pi _1(X')\to \mathbb {Z}$
maps x to zero and y to one and so, as before, there is a one-relator tree domain
$\pi _1(X')\to \mathbb {Z}$
maps x to zero and y to one and so, as before, there is a one-relator tree domain
![]() $Z'\subset Y'\looparrowright X'$
such that
$Z'\subset Y'\looparrowright X'$
such that
![]() $-1\cdot Z'\cap Z'\cap 1\cdot Z'$
is connected. There is also an induced homotopy equivalence between
$-1\cdot Z'\cap Z'\cap 1\cdot Z'$
is connected. There is also an induced homotopy equivalence between
![]() $Z'$
and a one-relator subcomplex of Y. In particular, we see that we must have
$Z'$
and a one-relator subcomplex of Y. In particular, we see that we must have
Therefore, this implies that
![]() $X'$
is a presentation complex of a primitive extension group of the form (5.1) or (5.2).
$X'$
is a presentation complex of a primitive extension group of the form (5.1) or (5.2).
Before proving our main theorem, we first mention some examples of one-relator groups that are primitive extension groups.
Example 5.3 If
![]() $p, q> 0$
are coprime integers, then
$p, q> 0$
are coprime integers, then
Example 5.4 A one-relator group
![]() $\langle a, b \mid w \rangle $
in which
$\langle a, b \mid w \rangle $
in which
![]() $\langle a\rangle \cap \langle b\rangle \neq 1$
is a primitive extension group by Lemma 4.5. More concretely, for all nonzero integers
$\langle a\rangle \cap \langle b\rangle \neq 1$
is a primitive extension group by Lemma 4.5. More concretely, for all nonzero integers
![]() $m, n$
, the one-relator group
$m, n$
, the one-relator group
![]() $\langle a, b \mid a^m = b^n\rangle $
is a primitive extension group.
$\langle a, b \mid a^m = b^n\rangle $
is a primitive extension group.
Example 5.5 Any one-relator group that splits as an ascending HNN-extension of a finitely generated free group (or in other words, has nontrivial BNS invariant) is a primitive extension group for the following reason: if X is a one-relator complex, then by Brown’s criterion [Reference BrownBro87],
![]() $\pi _1(X)$
splits as an ascending HNN-extension of a free group if and only if there is a one-relator tower
$\pi _1(X)$
splits as an ascending HNN-extension of a free group if and only if there is a one-relator tower
![]() $Z\looparrowright X$
such that
$Z\looparrowright X$
such that
![]() $\pi _1(Z) = \pi _1(Z\cap 1\cdot Z)$
or
$\pi _1(Z) = \pi _1(Z\cap 1\cdot Z)$
or
![]() $\pi _1(Z) = \pi _1(-1\cdot Z\cap Z)$
(see also [Reference LintonLin22a, Section 5.3]). Thus, when
$\pi _1(Z) = \pi _1(-1\cdot Z\cap Z)$
(see also [Reference LintonLin22a, Section 5.3]). Thus, when
![]() $\pi _1(X)$
has nontrivial BNS invariant,
$\pi _1(X)$
has nontrivial BNS invariant,
![]() $\pi _1(Z)$
has an exceptional intersection and is free, so X is a primitive extension complex. In fact, all such one-relator groups correspond to the subfamily
$\pi _1(Z)$
has an exceptional intersection and is free, so X is a primitive extension complex. In fact, all such one-relator groups correspond to the subfamily
![]() $E_{p}(a, y)$
.
$E_{p}(a, y)$
.
Theorem 5.6 A one-relator group is hyperbolic (and virtually special) if its primitive extension subgroups are hyperbolic (and virtually special).
Proof Let G be a one-relator group. Suppose that all primitive extension subgroups of G are hyperbolic (and virtually special). Since
![]() $\operatorname {\mathrm {BS}}(1, n)$
is a primitive extension group and all Baumslag–Solitar groups contain some
$\operatorname {\mathrm {BS}}(1, n)$
is a primitive extension group and all Baumslag–Solitar groups contain some
![]() $\operatorname {\mathrm {BS}}(1, n)$
as a subgroup, G contains no Baumslag–Solitar subgroup. Now, by Corollary 4.9 and Lemma 5.2, it follows that G is hyperbolic (and virtually special).
$\operatorname {\mathrm {BS}}(1, n)$
as a subgroup, G contains no Baumslag–Solitar subgroup. Now, by Corollary 4.9 and Lemma 5.2, it follows that G is hyperbolic (and virtually special).
It is now immediate that in order to characterize hyperbolic one-relator groups, one only needs to characterize hyperbolic primitive extension groups.
Corollary 5.7 Gersten’s conjecture is true if it is true for primitive extension groups.
Acknowledgements
The author would like to thank Saul Schleimer for many helpful conversations, in particular for pointing him in the direction of Christoffel words. He would also like to thank the anonymous referee for helpful comments. A large part of the work in this article also appears in the author’s PhD thesis, completed at the University of Warwick.