1 Introduction
1.1 Motivations and overviews
One of the fundamental results in the theory of affine groups states that the category of affine abelian groups is an abelian category, where epimorphisms are faithfully flat morphisms and monomorphism are closed immersions [Reference Demazure and Gabriel10, Chapter III, Section 3, no. 7, Paragraph 7.4, Corollaire, p. 355]. A purely algebraic proof of this theorem was given by Takeuchi in [Reference Takeuchi36, Corollary 4.16], which asserts, in algebraic terms, that the category of commutative and cocommutative Hopf algebras over a field
![]() $\Bbbk $
is an abelian category, hereby generalizing a well-known result from Grothendieck, who proved the same result under the additional condition of finite dimensionality. The main ingredient in Takeuchi’s proof is a Galois-type one-to-one correspondence between all sub-Hopf algebras and all normal Hopf ideals of a given commutative Hopf algebra. This bijection associates any sub-Hopf algebra with the ideal generated by the kernel of its counit. It is noteworthy that injectivity follows from the fact that any Hopf algebra is faithfully flat over its arbitrary sub-Hopf algebras [Reference Takeuchi36, Theorem 3.1]. The same correspondence can be found in [Reference Abe1, Section 4, p. 201], although with a slightly different proof. This correspondence does not rely on commutativity or cocommutativity of the Hopf algebras, and allowed, for example, to an extension of Takeuchi’s result showing that the category of cocommutative (but not necessarily commutative) Hopf algebras is semi-abelian [Reference Gran, Sterck and Vercruysse22].
$\Bbbk $
is an abelian category, hereby generalizing a well-known result from Grothendieck, who proved the same result under the additional condition of finite dimensionality. The main ingredient in Takeuchi’s proof is a Galois-type one-to-one correspondence between all sub-Hopf algebras and all normal Hopf ideals of a given commutative Hopf algebra. This bijection associates any sub-Hopf algebra with the ideal generated by the kernel of its counit. It is noteworthy that injectivity follows from the fact that any Hopf algebra is faithfully flat over its arbitrary sub-Hopf algebras [Reference Takeuchi36, Theorem 3.1]. The same correspondence can be found in [Reference Abe1, Section 4, p. 201], although with a slightly different proof. This correspondence does not rely on commutativity or cocommutativity of the Hopf algebras, and allowed, for example, to an extension of Takeuchi’s result showing that the category of cocommutative (but not necessarily commutative) Hopf algebras is semi-abelian [Reference Gran, Sterck and Vercruysse22].
The aim of this research is to extend the aforementioned correspondence to the “multi-object” setting, that is, from (affine) groups to (affine) groupoids. In Hopf algebraic terms, groupoids can be described as weak Hopf algebras or Hopf algebroids. We will therefore first provide a Galois correspondence between (certain classes of) Hopf ideals and sub-Hopf algebroids of general Hopf algebroids (in fact, even bialgebroids), and specializing to the commutative case, we obtain results for affine groupoids. Similar to the classical case explained above, the motivation of this work is that it could lead ultimately to a better understanding of the exactness properties of the category of (abelian) affine
![]() $\Bbbk $
-groupoids. Furthermore, our results have applications on a wide variety of topics, since the interest in Hopf algebroids is widespread in different branches of mathematics: from algebraic topology, algebraic geometry, and differential geometry (see [Reference Deligne, Cartier, Katz, Manin, Illusie, Laumon and Ribet9, Reference El Kaoutit and Saracco16, Reference Ravenel31]), to the study of linear differential equations (see [Reference El Kaoutit and Gómez-Torrecillas14, Reference El Kaoutit and Saracco17]), noncommutative differential calculus [Reference Ghobadi18], and in the study of the fundamental groupoid of quivers [Reference Ghobadi19], to mention only a few.
$\Bbbk $
-groupoids. Furthermore, our results have applications on a wide variety of topics, since the interest in Hopf algebroids is widespread in different branches of mathematics: from algebraic topology, algebraic geometry, and differential geometry (see [Reference Deligne, Cartier, Katz, Manin, Illusie, Laumon and Ribet9, Reference El Kaoutit and Saracco16, Reference Ravenel31]), to the study of linear differential equations (see [Reference El Kaoutit and Gómez-Torrecillas14, Reference El Kaoutit and Saracco17]), noncommutative differential calculus [Reference Ghobadi18], and in the study of the fundamental groupoid of quivers [Reference Ghobadi19], to mention only a few.
1.2 Description of the main results
Recall that a left Hopf algebroid over
![]() $\Bbbk $
(in the sense of Schauenburg [Reference Schauenburg34]) is a pair
$\Bbbk $
(in the sense of Schauenburg [Reference Schauenburg34]) is a pair
![]() $(A, {\mathcal H})$
of
$(A, {\mathcal H})$
of
![]() $\Bbbk $
-algebras together with a family of structure maps that make of
$\Bbbk $
-algebras together with a family of structure maps that make of
![]() ${\mathcal H}$
an
${\mathcal H}$
an
![]() $A\otimes _{}A^{o}$
-ring and an A-coring in a compatible way (see Definition 2.1) and whose Hopf–Galois map (described in equation (3.16)) is bijective. The so-called translation map
$A\otimes _{}A^{o}$
-ring and an A-coring in a compatible way (see Definition 2.1) and whose Hopf–Galois map (described in equation (3.16)) is bijective. The so-called translation map
![]() $\gamma :{\mathcal H}\to {\mathcal H}\times _{A^o}{\mathcal H}$
is obtained from the inverse of the Hopf–Galois map, and it is explicitly defined in equation (3.17). For a ring B over which a Hopf algebroid
$\gamma :{\mathcal H}\to {\mathcal H}\times _{A^o}{\mathcal H}$
is obtained from the inverse of the Hopf–Galois map, and it is explicitly defined in equation (3.17). For a ring B over which a Hopf algebroid
![]() $(A, {\mathcal H})$
coacts, we will denote the subring of coinvariant elements by
$(A, {\mathcal H})$
coacts, we will denote the subring of coinvariant elements by
![]() ${B}^{\textsf {co}{{\mathcal H}}}$
, and for any subset
${B}^{\textsf {co}{{\mathcal H}}}$
, and for any subset
![]() ${\mathcal K}$
of
${\mathcal K}$
of
![]() ${\mathcal H}$
, the symbol
${\mathcal H}$
, the symbol
![]() ${\mathcal K}^{+}$
stands for the intersection of the kernel of the counit of
${\mathcal K}^{+}$
stands for the intersection of the kernel of the counit of
![]() ${\mathcal H}$
with
${\mathcal H}$
with
![]() ${\mathcal K}$
. Finally, recall that a functor
${\mathcal K}$
. Finally, recall that a functor
![]() ${\mathcal L} \colon {\mathcal C} \to {\mathcal D}$
admitting a right adjoint
${\mathcal L} \colon {\mathcal C} \to {\mathcal D}$
admitting a right adjoint
![]() ${\mathcal R}$
is said to be comonadic if the comparison functor
${\mathcal R}$
is said to be comonadic if the comparison functor
![]() ${\mathcal K} \colon {\mathcal C} \to {\mathcal D}^{{\mathcal L}{\mathcal R}}$
to the Eilenberg–Moore category of coalgebras for the comonad
${\mathcal K} \colon {\mathcal C} \to {\mathcal D}^{{\mathcal L}{\mathcal R}}$
to the Eilenberg–Moore category of coalgebras for the comonad
![]() ${\mathcal L}{\mathcal R}$
is an equivalence.
${\mathcal L}{\mathcal R}$
is an equivalence.
With these notations at hand, our first main result in the general context of noncommutative Hopf algebroids is the following. The functor
![]() ${\mathcal H} \otimes _{B} -$
in the statement below denotes the extension of scalars functor
${\mathcal H} \otimes _{B} -$
in the statement below denotes the extension of scalars functor
![]() ${_B\textsf {Mod}}\to {_{{\mathcal H}}\textsf {Mod}}$
.
${_B\textsf {Mod}}\to {_{{\mathcal H}}\textsf {Mod}}$
.
Theorem A (Theorem 3.15)
Let
![]() $(A,{\mathcal H})$
be a left Hopf algebroid over
$(A,{\mathcal H})$
be a left Hopf algebroid over
![]() $\Bbbk $
such that
$\Bbbk $
such that
![]() ${{}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}}$
is A-flat. We have a well-defined inclusion-preserving bijective correspondence
${{}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}}$
is A-flat. We have a well-defined inclusion-preserving bijective correspondence

When specialized to the commutative setting, it induces our second main theorem.
Theorem B (Theorem 4.26)
Let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid such that
$(A,{\mathcal H})$
be a commutative Hopf algebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat. Then we have a well-defined inclusion-preserving bijective correspondence
${}_{s} {{{\mathcal H}}}$
is A-flat. Then we have a well-defined inclusion-preserving bijective correspondence

Given a commutative
![]() $\Bbbk $
-algebra A, we denote by
$\Bbbk $
-algebra A, we denote by
![]() $\mathscr {G}_A$
the associated
$\mathscr {G}_A$
the associated
![]() $\Bbbk $
-functor, that is, the functor from all commutative
$\Bbbk $
-functor, that is, the functor from all commutative
![]() $\Bbbk $
-algebras to sets that sends any algebra C the set of all algebra maps from A to C. In this way, a commutative Hopf algebroid
$\Bbbk $
-algebras to sets that sends any algebra C the set of all algebra maps from A to C. In this way, a commutative Hopf algebroid
![]() $(A,{\mathcal H})$
gives rise to the pair of
$(A,{\mathcal H})$
gives rise to the pair of
![]() $\Bbbk $
-functors
$\Bbbk $
-functors
![]() $(\mathscr {G}_A, \mathscr {G}_{{\mathcal H}})$
which form a presheaf of groupoids (i.e., an affine
$(\mathscr {G}_A, \mathscr {G}_{{\mathcal H}})$
which form a presheaf of groupoids (i.e., an affine
![]() $\Bbbk $
-groupoid scheme). If, as a working terminology, we say that a subgroupoid
$\Bbbk $
-groupoid scheme). If, as a working terminology, we say that a subgroupoid
![]() $\left (\mathscr {G}_A,\mathscr {G}_{\frac {{\mathcal H}}{I}}\right )$
of a given groupoid
$\left (\mathscr {G}_A,\mathscr {G}_{\frac {{\mathcal H}}{I}}\right )$
of a given groupoid
![]() $\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
is pure whenever the extension
$\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
is pure whenever the extension
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}} \subseteq {\mathcal H}$
is pure, then Theorem B can be rephrased as follows.
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}} \subseteq {\mathcal H}$
is pure, then Theorem B can be rephrased as follows.
Proposition C Let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid such that
$(A,{\mathcal H})$
be a commutative Hopf algebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat. Then we have an inclusion-preserving bijective correspondence
${}_{s} {{{\mathcal H}}}$
is A-flat. Then we have an inclusion-preserving bijective correspondence
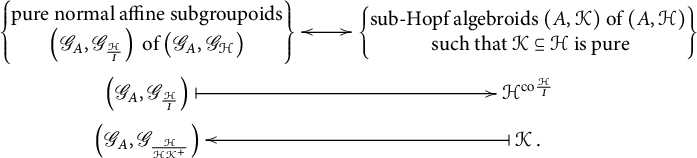
A concrete application of the above to the Hopf algebroid of functions on a finite groupoid (i.e., with a finite set of arrows) is detailed in Example 4.27, where we show that there is a bijective correspondence between normal subgroupoids of a finite groupoid and pure sub-Hopf algebroids of the associated Hopf algebroid of functions.
As a consequence of our main theorem, we have the following remarkable result.
Proposition D (Corollaries 4.32 and 4.33)
Let
![]() $\Bbbk $
be an algebraically closed field, and let
$\Bbbk $
be an algebraically closed field, and let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid over
$(A,{\mathcal H})$
be a commutative Hopf algebroid over
![]() $\Bbbk $
such that
$\Bbbk $
such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat.
${}_{s} {{{\mathcal H}}}$
is A-flat.
-
(a) If
 $\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{{\mathcal H}/I}(\Bbbk )\big )$
is a normal subgroupoid of
$\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{{\mathcal H}/I}(\Bbbk )\big )$
is a normal subgroupoid of
 $\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{\mathcal H}(\Bbbk )\big )$
such that
$\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{\mathcal H}(\Bbbk )\big )$
such that
 ${\mathcal H}$
is faithfully flat over
${\mathcal H}$
is faithfully flat over
 ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, then
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, then  $$ \begin{align*}\mathscr{G}_{\mathcal H}(\Bbbk) / \mathscr{G}_{{\mathcal H}/I}(\Bbbk) \ \cong \ \mathscr{G}_{{{\mathcal H}}^{\textsf{co}{({{\mathcal H}}/{I})}}}(\Bbbk).\end{align*} $$
$$ \begin{align*}\mathscr{G}_{\mathcal H}(\Bbbk) / \mathscr{G}_{{\mathcal H}/I}(\Bbbk) \ \cong \ \mathscr{G}_{{{\mathcal H}}^{\textsf{co}{({{\mathcal H}}/{I})}}}(\Bbbk).\end{align*} $$
-
(b) If
 $(A,{\mathcal K})$
is a sub-Hopf algebroid of the commutative Hopf algebroid
$(A,{\mathcal K})$
is a sub-Hopf algebroid of the commutative Hopf algebroid
 $(A,{\mathcal H})$
such that
$(A,{\mathcal H})$
such that
 ${\mathcal H}$
is faithfully flat over
${\mathcal H}$
is faithfully flat over
 ${\mathcal K}$
, then
${\mathcal K}$
, then  $$ \begin{align*}\mathscr{G}_{\mathcal H}(\Bbbk)/\mathscr{G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+}(\Bbbk) \ \cong \ \mathscr{G}_{{\mathcal K}}(\Bbbk).\end{align*} $$
$$ \begin{align*}\mathscr{G}_{\mathcal H}(\Bbbk)/\mathscr{G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+}(\Bbbk) \ \cong \ \mathscr{G}_{{\mathcal K}}(\Bbbk).\end{align*} $$
This result generalizes corresponding known results for affine algebraic groups (compare, for example, with [Reference Demazure and Gabriel10, Chapter III, Section 3, n°7, Théorème 7.2, p. 353, and Paragraph 7.3, Corollaire, p. 354]).
2 Preliminaries, notation, and first results
We work over a ground field
![]() $\Bbbk $
. All vector spaces, algebras, and coalgebras will be over
$\Bbbk $
. All vector spaces, algebras, and coalgebras will be over
![]() $\Bbbk $
. The unadorned tensor product
$\Bbbk $
. The unadorned tensor product
![]() $\otimes _{}$
stands for
$\otimes _{}$
stands for
![]() $\otimes _{\Bbbk }$
. By a ring, we always mean a ring with identity element and modules over rings or algebras are always assumed to be unital. All over the paper, we assume a certain familiarity of the reader with the language of monoidal categories and of (co)monoids therein (see, for example, [Reference MacLane28, Chapter VII]).
$\otimes _{\Bbbk }$
. By a ring, we always mean a ring with identity element and modules over rings or algebras are always assumed to be unital. All over the paper, we assume a certain familiarity of the reader with the language of monoidal categories and of (co)monoids therein (see, for example, [Reference MacLane28, Chapter VII]).
We begin by collecting some facts about bimodules, (co)rings, and bialgebroids that will be needed in the sequel. The aim is that of keeping the exposition self-contained. Many results and definitions we will present herein hold in a more general context and under less restrictive hypotheses, but we preferred to limit ourselves to the essentials.
Given a (preferably, noncommutative)
![]() $\Bbbk $
-algebra A, the category of A-bimodules forms a nonstrict monoidal category
$\Bbbk $
-algebra A, the category of A-bimodules forms a nonstrict monoidal category
![]() $\left ({}_{A}{\textsf {Mod}}_{A},\otimes _{A},A,\mathfrak {a},\mathfrak {l},\mathfrak {r}\right )$
. Nevertheless, all over the paper, we will behave as if the structural natural isomorphisms
$\left ({}_{A}{\textsf {Mod}}_{A},\otimes _{A},A,\mathfrak {a},\mathfrak {l},\mathfrak {r}\right )$
. Nevertheless, all over the paper, we will behave as if the structural natural isomorphisms
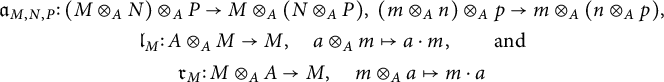 $$ \begin{gather*} \mathfrak{a}_{M,N,P} \colon (M\otimes_{A}N)\otimes_{A}P \to M\otimes_{A}(N\otimes_{A}P), \ (m\otimes_{A}n)\otimes_{A}p \to m\otimes_{A}(n\otimes_{A}p), \\ \mathfrak{l}_M \colon A \otimes_{A} M \to M, \quad a\otimes_{A}m \mapsto a\cdot m, \qquad \text{and} \\ \mathfrak{r}_M \colon M\otimes_{A}A \to M, \quad m \otimes_{A} a \mapsto m \cdot a \end{gather*} $$
$$ \begin{gather*} \mathfrak{a}_{M,N,P} \colon (M\otimes_{A}N)\otimes_{A}P \to M\otimes_{A}(N\otimes_{A}P), \ (m\otimes_{A}n)\otimes_{A}p \to m\otimes_{A}(n\otimes_{A}p), \\ \mathfrak{l}_M \colon A \otimes_{A} M \to M, \quad a\otimes_{A}m \mapsto a\cdot m, \qquad \text{and} \\ \mathfrak{r}_M \colon M\otimes_{A}A \to M, \quad m \otimes_{A} a \mapsto m \cdot a \end{gather*} $$
were “the identities,” that is, as if
![]() ${}_{A}{\textsf {Mod}}_{A}$
was a strict monoidal category. If A is a noncommutative algebra, then we denote by
${}_{A}{\textsf {Mod}}_{A}$
was a strict monoidal category. If A is a noncommutative algebra, then we denote by
![]() $A^{\mathrm {o}}$
its opposite algebra. In this case, an element
$A^{\mathrm {o}}$
its opposite algebra. In this case, an element
![]() $a \in A$
may be denoted by
$a \in A$
may be denoted by
![]() $a^{\mathrm {o}}$
when it is helpful to stress that it is viewed as an element in
$a^{\mathrm {o}}$
when it is helpful to stress that it is viewed as an element in
![]() $A^{\mathrm {o}}$
. We freely use the canonical isomorphism between the category of left A-module
$A^{\mathrm {o}}$
. We freely use the canonical isomorphism between the category of left A-module
![]() ${}_{A}\textsf {Mod}$
and that of right
${}_{A}\textsf {Mod}$
and that of right
![]() $A^{\mathrm {o}}$
-modules
$A^{\mathrm {o}}$
-modules
![]() $\textsf {Mod}_{A^{\mathrm {o}}}$
.
$\textsf {Mod}_{A^{\mathrm {o}}}$
.
2.1 The enveloping algebra and bimodules
Let A be an algebra, we denote by
![]() the enveloping algebra of A, and we identify the category
the enveloping algebra of A, and we identify the category
![]() ${}_{A^{\mathrm {e}}}\textsf {Mod}$
of left
${}_{A^{\mathrm {e}}}\textsf {Mod}$
of left
![]() $A^{\mathrm {e}}$
-modules with the category
$A^{\mathrm {e}}$
-modules with the category
![]() ${}_{A}{\textsf { Mod}}_{A}$
of A-bimodules. Giving a morphism of algebras
${}_{A}{\textsf { Mod}}_{A}$
of A-bimodules. Giving a morphism of algebras
![]() $A^{\mathrm {e}} \to R$
is equivalent to providing two commuting algebra maps
$A^{\mathrm {e}} \to R$
is equivalent to providing two commuting algebra maps
![]() $s\colon A \to R$
and
$s\colon A \to R$
and
![]() $t\colon A^{\mathrm {o}} \to R$
, called the source and the target, respectively. In particular, the identity of
$t\colon A^{\mathrm {o}} \to R$
, called the source and the target, respectively. In particular, the identity of
![]() $A^{\mathrm {e}}$
gives rise to
$A^{\mathrm {e}}$
gives rise to
![]() $s\colon A \to A^{\mathrm {e}}, a \mapsto a \otimes 1^{\mathrm {o}}$
and
$s\colon A \to A^{\mathrm {e}}, a \mapsto a \otimes 1^{\mathrm {o}}$
and
![]() $t\colon A^{\mathrm {o}} \to A^{\mathrm {e}}, a^{\mathrm {o}} \mapsto 1 \otimes a^{\mathrm {o}}$
.
$t\colon A^{\mathrm {o}} \to A^{\mathrm {e}}, a^{\mathrm {o}} \mapsto 1 \otimes a^{\mathrm {o}}$
.
Given two
![]() $A^{\mathrm {e}}$
-bimodules M and N, there are several A-bimodule structures underlying M and N. Namely,
$A^{\mathrm {e}}$
-bimodules M and N, there are several A-bimodule structures underlying M and N. Namely,
for all
![]() $m \in M$
,
$m \in M$
,
![]() $a,b,c,d\in A$
. This leads to several ways of considering the tensor product over A between these underlying A-bimodules. For the sake of clarity, we will adopt the following notations. Given an
$a,b,c,d\in A$
. This leads to several ways of considering the tensor product over A between these underlying A-bimodules. For the sake of clarity, we will adopt the following notations. Given an
![]() $A^{\mathrm {e}}$
-bimodule M, the A-action by elements of the form
$A^{\mathrm {e}}$
-bimodule M, the A-action by elements of the form
![]() $a\otimes _{}1^{\mathrm {o}}$
will be denoted by
$a\otimes _{}1^{\mathrm {o}}$
will be denoted by
![]() ${}_{s} {M}$
or
${}_{s} {M}$
or
![]() ${M}{}_{s} $
and the
${M}{}_{s} $
and the
![]() $A^{\mathrm {o}}$
-action of the element of the form
$A^{\mathrm {o}}$
-action of the element of the form
![]() $1\otimes _{}a^{\mathrm {o}}$
by
$1\otimes _{}a^{\mathrm {o}}$
by
![]() ${}_{t} {M}$
or
${}_{t} {M}$
or
![]() ${M}{}_{t}$
, depending on which side we are putting those elements. We still have other actions by the elements
${M}{}_{t}$
, depending on which side we are putting those elements. We still have other actions by the elements
![]() $t(a)^{\mathrm {o}}$
, or
$t(a)^{\mathrm {o}}$
, or
![]() $s(a)^{\mathrm {o}}$
to produce other A or
$s(a)^{\mathrm {o}}$
to produce other A or
![]() $A^{\mathrm {o}}$
actions. In this case, we use the notation
$A^{\mathrm {o}}$
actions. In this case, we use the notation
![]() $t^{\mathrm {o}}$
and
$t^{\mathrm {o}}$
and
![]() $s^{\mathrm {o}}$
located in the corresponding side on which we are declaring the action. Summing up, we denote
$s^{\mathrm {o}}$
located in the corresponding side on which we are declaring the action. Summing up, we denote
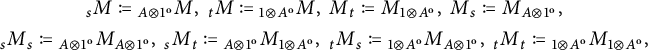
from which we can switch the given actions and obtain new two-sided actions involving A and
![]() $A^{\mathrm {o}}$
:
$A^{\mathrm {o}}$
:
and so on. For example,
![]() ${M}{}_{t^{\mathrm {o}}} = {}_{t} {M}$
. For the sake of simplicity, we may also often resort to the following variation of the previous conventions: for
${M}{}_{t^{\mathrm {o}}} = {}_{t} {M}$
. For the sake of simplicity, we may also often resort to the following variation of the previous conventions: for
![]() $a,b \in A$
,
$a,b \in A$
,
![]() $m \in M$
,
$m \in M$
,
2.2 Pure extensions of rings
Purity conditions will play a crucial role in establishing our main theorems. Therefore, we devote this subsection to collect a few results in details in this regard, for the convenience of the reader.
Given a ring R, we recall from [Reference Bourbaki4, Chapter I, Section 2, Example 24, p. 66] that a morphism of left (resp. right) R-modules
![]() $f\colon M \to N$
is called pure (or universally injective) if and only if, for every right (resp. left) R-module P, the morphism of abelian groups
$f\colon M \to N$
is called pure (or universally injective) if and only if, for every right (resp. left) R-module P, the morphism of abelian groups
![]() $P \otimes _{R} f$
(resp.
$P \otimes _{R} f$
(resp.
![]() $f \otimes _{R} P$
) is injective. In particular, f itself is injective, by taking
$f \otimes _{R} P$
) is injective. In particular, f itself is injective, by taking
![]() $P = R$
.
$P = R$
.
Proposition 2.1 (and its corollaries) should be well known: it states that a ring extension
![]() $f \colon {\mathcal A} \to {\mathcal B}$
is pure as a morphism of right
$f \colon {\mathcal A} \to {\mathcal B}$
is pure as a morphism of right
![]() ${\mathcal A}$
-modules if and only if the extension-of-scalars functor
${\mathcal A}$
-modules if and only if the extension-of-scalars functor
![]() ${\mathcal B} \otimes _{{\mathcal A}} -$
is faithful. They will be of great help in what follows.
${\mathcal B} \otimes _{{\mathcal A}} -$
is faithful. They will be of great help in what follows.
Proposition 2.1 Let R be a ring, and let
![]() $f \colon {\mathcal A} \to {\mathcal B}$
be a morphism of R-rings. The following are equivalent.
$f \colon {\mathcal A} \to {\mathcal B}$
be a morphism of R-rings. The following are equivalent.
-
(1)
 $f \colon {\mathcal A} \to {\mathcal B}$
is a pure morphism of right
$f \colon {\mathcal A} \to {\mathcal B}$
is a pure morphism of right
 ${\mathcal A}$
-modules.
${\mathcal A}$
-modules. -
(2) For every left
 ${\mathcal A}$
-module M, the morphism
${\mathcal A}$
-module M, the morphism
 $\varrho _M\colon M \to {\mathcal B} \otimes _{{\mathcal A}} M$
,
$\varrho _M\colon M \to {\mathcal B} \otimes _{{\mathcal A}} M$
,
 $m \mapsto 1_{\mathcal B} \otimes _{{\mathcal A}} m$
, is injective for all
$m \mapsto 1_{\mathcal B} \otimes _{{\mathcal A}} m$
, is injective for all
 $m \in M$
.
$m \in M$
. -
(3) For every morphism of left
 ${\mathcal A}$
-modules
${\mathcal A}$
-modules
 $g \colon M \to N$
,
$g \colon M \to N$
,
 ${\mathcal B} \otimes _{{\mathcal A}} g = 0$
implies
${\mathcal B} \otimes _{{\mathcal A}} g = 0$
implies
 $g = 0$
.
$g = 0$
. -
(4) If
 $M \xrightarrow {g} N \xrightarrow {h} P$
are morphisms of left
$M \xrightarrow {g} N \xrightarrow {h} P$
are morphisms of left
 ${\mathcal A}$
-modules such that
${\mathcal A}$
-modules such that  $$ \begin{align*}{\mathcal B} \otimes_{{\mathcal A}} M \xrightarrow{{\mathcal B} \otimes_{{\mathcal A}} g} {\mathcal B} \otimes_{{\mathcal A}} N \xrightarrow{{\mathcal B} \otimes_{{\mathcal A}} h} {\mathcal B} \otimes_{{\mathcal A}} P\end{align*} $$
$$ \begin{align*}{\mathcal B} \otimes_{{\mathcal A}} M \xrightarrow{{\mathcal B} \otimes_{{\mathcal A}} g} {\mathcal B} \otimes_{{\mathcal A}} N \xrightarrow{{\mathcal B} \otimes_{{\mathcal A}} h} {\mathcal B} \otimes_{{\mathcal A}} P\end{align*} $$
is an exact sequence of
 ${\mathcal B}$
-modules, then
${\mathcal B}$
-modules, then
 $M \xrightarrow {g} N \xrightarrow {h} P$
is an exact sequence of
$M \xrightarrow {g} N \xrightarrow {h} P$
is an exact sequence of
 ${\mathcal A}$
-modules.
${\mathcal A}$
-modules. -
(5) If
 $g \colon M \to N$
is a morphism of left
$g \colon M \to N$
is a morphism of left
 ${\mathcal A}$
-modules such that
${\mathcal A}$
-modules such that
 ${\mathcal B} \otimes _{{\mathcal A}} g \colon {\mathcal B} \otimes _{{\mathcal A}} M \to {\mathcal B} \otimes _{{\mathcal A}} N$
is injective, then g itself is injective.
${\mathcal B} \otimes _{{\mathcal A}} g \colon {\mathcal B} \otimes _{{\mathcal A}} M \to {\mathcal B} \otimes _{{\mathcal A}} N$
is injective, then g itself is injective.
In addition, any of the foregoing entails that
-
(6) for every left ideal
 $\mathfrak {m}$
in
$\mathfrak {m}$
in
 ${\mathcal A}$
, we have
${\mathcal A}$
, we have
 $\mathfrak {m} = f^{-1}({\mathcal B}\mathfrak {m})$
,
$\mathfrak {m} = f^{-1}({\mathcal B}\mathfrak {m})$
,
and hence, in particular, that
-
(7) for every maximal left ideal
 $\mathfrak {m}$
in
$\mathfrak {m}$
in
 ${\mathcal A}$
, there exists a maximal left ideal
${\mathcal A}$
, there exists a maximal left ideal
 $\mathfrak {n}$
in
$\mathfrak {n}$
in
 ${\mathcal B}$
such that
${\mathcal B}$
such that
 $\mathfrak {m} = f^{-1}(\mathfrak {n})$
.
$\mathfrak {m} = f^{-1}(\mathfrak {n})$
.
Proof The equivalence between (1) and (2) is the definition of purity. The equivalence between (3) and (4) is the fact that an additive covariant functor between abelian categories is faithful if and only if it reflects exact sequences (see [Reference Popescu30, Section 3.1, Exercise 4]). The implication from (2) to (3) follows by commutativity of the diagram
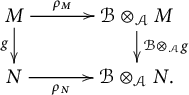
To prove that (4) implies (5), consider the morphisms
![]() $0 \to M \xrightarrow {g} N$
and apply the functor
$0 \to M \xrightarrow {g} N$
and apply the functor
![]() ${\mathcal B} \otimes _{{\mathcal A}} -$
. The implication from (5) to (2) follows by considering the morphism
${\mathcal B} \otimes _{{\mathcal A}} -$
. The implication from (5) to (2) follows by considering the morphism
and observing that it admits the retraction
whence it is injective. Finally, let us show that (2)
![]() $\Rightarrow $
(6)
$\Rightarrow $
(6)
![]() $\Rightarrow $
(7). To prove that (2) implies (6), let
$\Rightarrow $
(7). To prove that (2) implies (6), let
![]() $\mathfrak {m}$
be a left ideal in
$\mathfrak {m}$
be a left ideal in
![]() ${\mathcal A}$
. Since
${\mathcal A}$
. Since
![]() ${\mathcal A}/\mathfrak {m}$
is a left
${\mathcal A}/\mathfrak {m}$
is a left
![]() ${\mathcal A}$
-module, (2) entails that
${\mathcal A}$
-module, (2) entails that
is injective and therefore
![]() $\mathfrak {m} = f^{-1}({\mathcal B}\mathfrak {m})$
. Now, to show that (6) implies (7), observe that, by taking
$\mathfrak {m} = f^{-1}({\mathcal B}\mathfrak {m})$
. Now, to show that (6) implies (7), observe that, by taking
![]() $\mathfrak {m} = 0$
in (6), we know that f is injective, and hence we may assume that
$\mathfrak {m} = 0$
in (6), we know that f is injective, and hence we may assume that
![]() ${\mathcal A} \subseteq {\mathcal B}$
. Suppose that
${\mathcal A} \subseteq {\mathcal B}$
. Suppose that
![]() $\mathfrak {m}$
is a maximal ideal in
$\mathfrak {m}$
is a maximal ideal in
![]() ${\mathcal A}$
, and let
${\mathcal A}$
, and let
![]() $\mathfrak {n} \subset {\mathcal B}$
be a maximal ideal containing
$\mathfrak {n} \subset {\mathcal B}$
be a maximal ideal containing
![]() ${\mathcal B} \mathfrak {m}$
. Then
${\mathcal B} \mathfrak {m}$
. Then
![]() $\mathfrak {m} = f^{-1}({\mathcal B}\mathfrak {m}) \subseteq f^{-1}(\mathfrak {n})$
and so, since
$\mathfrak {m} = f^{-1}({\mathcal B}\mathfrak {m}) \subseteq f^{-1}(\mathfrak {n})$
and so, since
![]() $1 \notin \mathfrak {n}$
,
$1 \notin \mathfrak {n}$
,
![]() $\mathfrak {m} = f^{-1}(\mathfrak {n})$
by maximality of
$\mathfrak {m} = f^{-1}(\mathfrak {n})$
by maximality of
![]() $\mathfrak {m}$
.
$\mathfrak {m}$
.
Proposition 2.1 is the analog of [Reference Bourbaki4, Chapter I, Section 3, n°5, Proposition 9] and [Reference Waterhouse39, Section 13.1, Theorem] for pure morphisms.
Corollary 2.2 (of Proposition 2.1)
Let R be a ring, and let
![]() $f \colon {\mathcal A} \to {\mathcal B}$
be a morphism of R-rings. If f is pure as a morphism of right
$f \colon {\mathcal A} \to {\mathcal B}$
be a morphism of R-rings. If f is pure as a morphism of right
![]() ${\mathcal A}$
-modules, then
${\mathcal A}$
-modules, then
![]() $(M,\varrho _M)$
is the equalizer of the pair
$(M,\varrho _M)$
is the equalizer of the pair
in the category of left
![]() ${\mathcal A}$
-modules, for every left
${\mathcal A}$
-modules, for every left
![]() ${\mathcal A}$
-module M. In particular, we have the equalizer
${\mathcal A}$
-module M. In particular, we have the equalizer
Proof Consider the parallel arrows
It is clear that the function
lands in the equalizer of
![]() ${\mathcal B} \otimes _{{\mathcal A}} \lambda _{\mathcal B} \otimes _{{\mathcal A}} M$
and
${\mathcal B} \otimes _{{\mathcal A}} \lambda _{\mathcal B} \otimes _{{\mathcal A}} M$
and
![]() ${\mathcal B} \otimes _{{\mathcal A}} \varrho _{\mathcal B} \otimes _{{\mathcal A}} M$
, and it is injective, since it admits
${\mathcal B} \otimes _{{\mathcal A}} \varrho _{\mathcal B} \otimes _{{\mathcal A}} M$
, and it is injective, since it admits
as a retraction. On the other hand, any
![]() $\sum _i b_i \otimes _{{\mathcal A}} b_i' \otimes _{{\mathcal A}} m_i$
in the equalizer satisfies
$\sum _i b_i \otimes _{{\mathcal A}} b_i' \otimes _{{\mathcal A}} m_i$
in the equalizer satisfies
![]() $\sum _i b_i \otimes _{{\mathcal A}} b_i' \otimes _{{\mathcal A}} m_i = \sum _i b_i b_i' \otimes _{{\mathcal A}} 1_{\mathcal B} \otimes _{{\mathcal A}} m_i$
, and hence it is in the image of
$\sum _i b_i \otimes _{{\mathcal A}} b_i' \otimes _{{\mathcal A}} m_i = \sum _i b_i b_i' \otimes _{{\mathcal A}} 1_{\mathcal B} \otimes _{{\mathcal A}} m_i$
, and hence it is in the image of
![]() ${\mathcal B} \otimes _{{\mathcal A}} \varrho _M$
. Therefore,
${\mathcal B} \otimes _{{\mathcal A}} \varrho _M$
. Therefore,
![]() $({\mathcal B} \otimes _{{\mathcal A}} M,{\mathcal B} \otimes _{{\mathcal A}} \varrho _M)$
is the equalizer of
$({\mathcal B} \otimes _{{\mathcal A}} M,{\mathcal B} \otimes _{{\mathcal A}} \varrho _M)$
is the equalizer of
![]() ${\mathcal B} \otimes _{{\mathcal A}} \lambda _{\mathcal B} \otimes _{{\mathcal A}} M$
and
${\mathcal B} \otimes _{{\mathcal A}} \lambda _{\mathcal B} \otimes _{{\mathcal A}} M$
and
![]() ${\mathcal B} \otimes _{{\mathcal A}} \varrho _{\mathcal B} \otimes _{{\mathcal A}} M$
, whence
${\mathcal B} \otimes _{{\mathcal A}} \varrho _{\mathcal B} \otimes _{{\mathcal A}} M$
, whence
![]() $(M,\varrho _M)$
is the equalizer of
$(M,\varrho _M)$
is the equalizer of
![]() $\lambda _{\mathcal B} \otimes _{{\mathcal A}} M$
and
$\lambda _{\mathcal B} \otimes _{{\mathcal A}} M$
and
![]() $\varrho _{\mathcal B} \otimes _{{\mathcal A}} M$
by purity (statement (4) in Proposition 2.1).
$\varrho _{\mathcal B} \otimes _{{\mathcal A}} M$
by purity (statement (4) in Proposition 2.1).
Corollary 2.3 (of Proposition 2.1)
Let R be a ring, and let
![]() $f \colon {\mathcal A} \to {\mathcal B}$
be a morphism of R-rings. If f is a pure morphism of right R-modules and
$f \colon {\mathcal A} \to {\mathcal B}$
be a morphism of R-rings. If f is a pure morphism of right R-modules and
![]() ${\mathcal B}_R$
is flat, then
${\mathcal B}_R$
is flat, then
![]() ${\mathcal A}_R$
is flat.
${\mathcal A}_R$
is flat.
Proof Take a monomorphism of left R-modules
![]() $M \xrightarrow {g} N$
. By flatness of
$M \xrightarrow {g} N$
. By flatness of
![]() ${\mathcal B}$
on R, we have that
${\mathcal B}$
on R, we have that
![]() ${\mathcal B} \otimes _{R} M \xrightarrow {{\mathcal B} \otimes _{R} g} {\mathcal B} \otimes _{R} N$
is injective and so
${\mathcal B} \otimes _{R} M \xrightarrow {{\mathcal B} \otimes _{R} g} {\mathcal B} \otimes _{R} N$
is injective and so
is injective, too. By purity (statement (5) in Proposition 2.1),
![]() ${\mathcal A} \otimes _{R} M \xrightarrow {{\mathcal A} \otimes _{R} g} {\mathcal A} \otimes _{R} N$
is injective.
${\mathcal A} \otimes _{R} M \xrightarrow {{\mathcal A} \otimes _{R} g} {\mathcal A} \otimes _{R} N$
is injective.
Corollary 2.4 (of Proposition 2.1)
Let R be any ring, and let
![]() ${\mathcal A} \xrightarrow {g} {\mathcal T} \xrightarrow {h} {\mathcal B}$
be morphisms of R-rings. Set
${\mathcal A} \xrightarrow {g} {\mathcal T} \xrightarrow {h} {\mathcal B}$
be morphisms of R-rings. Set
![]() . If
. If
![]() $f \colon {\mathcal A} \to {\mathcal B}$
is a pure morphism of right
$f \colon {\mathcal A} \to {\mathcal B}$
is a pure morphism of right
![]() ${\mathcal A}$
-modules, then the morphism of right R-modules g is pure as well. In particular, f is pure as a morphism of right R-modules.
${\mathcal A}$
-modules, then the morphism of right R-modules g is pure as well. In particular, f is pure as a morphism of right R-modules.
Proof Let P be any left R-module. Consider the morphism
Since it is split injective, with retraction induced by the multiplication of
![]() ${\mathcal B}$
, the morphism
${\mathcal B}$
, the morphism
is (split) injective as well, and hence
is injective. Since
then
![]() ${\mathcal B} \otimes _{{\mathcal A}} g \otimes _{R} P$
is injective, too. Being
${\mathcal B} \otimes _{{\mathcal A}} g \otimes _{R} P$
is injective, too. Being
![]() ${\mathcal B}_{\mathcal A}$
pure, the morphism
${\mathcal B}_{\mathcal A}$
pure, the morphism
![]() $g \otimes _{R} P$
is injective by statement (5) in Proposition 2.1. The last statement follows by taking f itself as g and
$g \otimes _{R} P$
is injective by statement (5) in Proposition 2.1. The last statement follows by taking f itself as g and
![]() $\operatorname {Id}_{\mathcal B}$
as h.
$\operatorname {Id}_{\mathcal B}$
as h.
Lemma 2.5 Let R be any ring, and let
![]() ${\mathcal A} \xrightarrow {g} {\mathcal T} \xrightarrow {h} {\mathcal B}$
be morphisms of R-rings. If
${\mathcal A} \xrightarrow {g} {\mathcal T} \xrightarrow {h} {\mathcal B}$
be morphisms of R-rings. If
![]() ${\mathcal B}_{\mathcal A}$
is faithfully flat, then the morphism of right R-modules g is pure. In particular,
${\mathcal B}_{\mathcal A}$
is faithfully flat, then the morphism of right R-modules g is pure. In particular,
![]() is pure.
is pure.
Proof Since a faithfully flat extension is pure, the statement follows from Corollary 2.4.
2.3 The Takeuchi–Sweedler crossed product
Let
![]() ${}_{A^{\mathrm {e}}}M{}_{A^{\mathrm {e}}}$
and
${}_{A^{\mathrm {e}}}M{}_{A^{\mathrm {e}}}$
and
![]() ${}_{A^{\mathrm {e}}}N{}_{A^{\mathrm {e}}}$
be two
${}_{A^{\mathrm {e}}}N{}_{A^{\mathrm {e}}}$
be two
![]() $A^{\mathrm {e}}$
-bimodules. We first define the A-bimodule
$A^{\mathrm {e}}$
-bimodules. We first define the A-bimodule
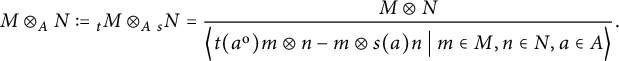
This will usually be the tensor product over A that we are going to consider more often, unless specified otherwise. Then, inside
![]() $M \otimes _{A} N$
, we consider the subspace
$M \otimes _{A} N$
, we consider the subspace
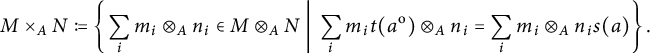
It is easy to see that
![]() $M \times _{A} N$
is an A-subbimodule (left
$M \times _{A} N$
is an A-subbimodule (left
![]() $A^{\mathrm {e}}$
-submodule) with respect to the actions
$A^{\mathrm {e}}$
-submodule) with respect to the actions
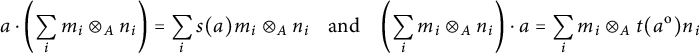 $$ \begin{align} a\cdot \left(\sum_i m_i \otimes_{A} n_i\right) = \sum_i s(a)m_i \otimes_{A} n_i \quad \!\text{and}\! \quad \left(\sum_i m_i \otimes_{A} n_i\right)\cdot a = \sum_i m_i \otimes_{A} t(a^{\mathrm{o}})n_i \end{align} $$
$$ \begin{align} a\cdot \left(\sum_i m_i \otimes_{A} n_i\right) = \sum_i s(a)m_i \otimes_{A} n_i \quad \!\text{and}\! \quad \left(\sum_i m_i \otimes_{A} n_i\right)\cdot a = \sum_i m_i \otimes_{A} t(a^{\mathrm{o}})n_i \end{align} $$
for all
![]() $\sum _i m_i \otimes _{A} n_i\in M\times _{A}N$
and
$\sum _i m_i \otimes _{A} n_i\in M\times _{A}N$
and
![]() $a\in A$
, but it is also an A-subbimodule (right
$a\in A$
, but it is also an A-subbimodule (right
![]() $A^{\mathrm {e}}$
-submodule) with respect to the actions
$A^{\mathrm {e}}$
-submodule) with respect to the actions
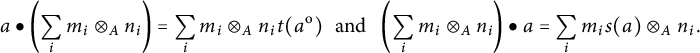 $$ \begin{align} a\bullet \left(\sum_i m_i \otimes_{A} n_i\kern-1pt\right) = \sum_i m_i \otimes_{A} n_it(a^{\mathrm{o}}) \!\!\!\quad \text{and}\!\!\! \quad \left(\sum_i m_i \otimes_{A} n_i\kern-1pt\right)\bullet a = \sum_i m_is(a) \otimes_{A} n_i. \end{align} $$
$$ \begin{align} a\bullet \left(\sum_i m_i \otimes_{A} n_i\kern-1pt\right) = \sum_i m_i \otimes_{A} n_it(a^{\mathrm{o}}) \!\!\!\quad \text{and}\!\!\! \quad \left(\sum_i m_i \otimes_{A} n_i\kern-1pt\right)\bullet a = \sum_i m_is(a) \otimes_{A} n_i. \end{align} $$
In particular, it is an
![]() $A^{\mathrm {e}}$
-bimodule itself. There exist categorical ways to describe this Takeuchi–Sweedler product in terms of ends and coends (see, e.g., [Reference Sweedler35, Reference Takeuchi37], where the integral notation dating back to [Reference Yoneda40] was used) or in terms of monoidal products (see, e.g., [Reference Böhm3, Reference Takeuchi38]), but, for the convenience of the unaccustomed reader and for the sake of simplicity, we decided to opt for the more elementary description above. In particular, in
$A^{\mathrm {e}}$
-bimodule itself. There exist categorical ways to describe this Takeuchi–Sweedler product in terms of ends and coends (see, e.g., [Reference Sweedler35, Reference Takeuchi37], where the integral notation dating back to [Reference Yoneda40] was used) or in terms of monoidal products (see, e.g., [Reference Böhm3, Reference Takeuchi38]), but, for the convenience of the unaccustomed reader and for the sake of simplicity, we decided to opt for the more elementary description above. In particular, in
![]() $M \times _{A} N$
, the following relations hold for all
$M \times _{A} N$
, the following relations hold for all
![]() $\sum _i m_i \otimes _{A} n_i \in M\times _{A} N$
and all
$\sum _i m_i \otimes _{A} n_i \in M\times _{A} N$
and all
![]() $a\in A$
:
$a\in A$
:
In this way, if
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() ${\mathcal V}$
are two
${\mathcal V}$
are two
![]() $A^{\mathrm {e}}$
-rings, then
$A^{\mathrm {e}}$
-rings, then
![]() ${\mathcal U} \times _{A} {\mathcal V}$
is also an
${\mathcal U} \times _{A} {\mathcal V}$
is also an
![]() $A^{\mathrm {e}}$
-ring, with multiplication
$A^{\mathrm {e}}$
-ring, with multiplication
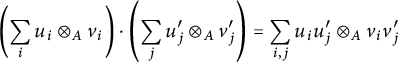 $$ \begin{align*}\left(\sum_iu_i \otimes_{A} v_i\right)\cdot \left(\sum_ju^{\prime}_j \otimes_{A} v^{\prime}_j\right) = \sum_{i,j}u_iu^{\prime}_j\otimes_{A}v_iv^{\prime}_j\end{align*} $$
$$ \begin{align*}\left(\sum_iu_i \otimes_{A} v_i\right)\cdot \left(\sum_ju^{\prime}_j \otimes_{A} v^{\prime}_j\right) = \sum_{i,j}u_iu^{\prime}_j\otimes_{A}v_iv^{\prime}_j\end{align*} $$
for all
![]() $u_i,u^{\prime }_j\in {\mathcal U}$
,
$u_i,u^{\prime }_j\in {\mathcal U}$
,
![]() $v_i,v^{\prime }_j\in {\mathcal V}$
and
$v_i,v^{\prime }_j\in {\mathcal V}$
and
![]() $\Bbbk $
-algebra morphism
$\Bbbk $
-algebra morphism
![]() $A\otimes _{}A^{o} \to {\mathcal U} \times _{A} {\mathcal V}, a \otimes b^{\mathrm {o}} \mapsto s_{\mathcal U}(a) \otimes _{A} t_{\mathcal V}\big (b^{\mathrm {o}}\big )$
. The
$A\otimes _{}A^{o} \to {\mathcal U} \times _{A} {\mathcal V}, a \otimes b^{\mathrm {o}} \mapsto s_{\mathcal U}(a) \otimes _{A} t_{\mathcal V}\big (b^{\mathrm {o}}\big )$
. The
![]() $A^{\mathrm {e}}$
-actions (2.4) and (2.5) are induced by this
$A^{\mathrm {e}}$
-actions (2.4) and (2.5) are induced by this
![]() $A^{\mathrm {e}}$
-ring structure.
$A^{\mathrm {e}}$
-ring structure.
2.4 Left bialgebroids
Next, we recall the definition of a left bialgebroid. It can be considered as a revised version of the notion of a
![]() $\times _A$
-bialgebra as it appears in [Reference Schauenburg33, Definition 4.3]. However, we prefer to mimic [Reference Lu25] as presented in [Reference Brzeziński and Militaru6, Definition 2.2].
$\times _A$
-bialgebra as it appears in [Reference Schauenburg33, Definition 4.3]. However, we prefer to mimic [Reference Lu25] as presented in [Reference Brzeziński and Militaru6, Definition 2.2].
Definition 2.1 A left bialgebroid is the datum of:
-
(B1) a pair
 $\left (A,{\mathcal H}\right )$
of
$\left (A,{\mathcal H}\right )$
of
 $\Bbbk $
-algebras;
$\Bbbk $
-algebras; -
(B2) a
 $\Bbbk $
-algebra map
$\Bbbk $
-algebra map
 , inducing a source
, inducing a source
 $s\colon A\to {\mathcal H}$
and a target
$s\colon A\to {\mathcal H}$
and a target
 $t\colon A^{\mathrm {o}}\to {\mathcal H}$
and making of
$t\colon A^{\mathrm {o}}\to {\mathcal H}$
and making of
 ${\mathcal H}$
an
${\mathcal H}$
an
 $A^{\mathrm {e}}$
-bimodule;
$A^{\mathrm {e}}$
-bimodule; -
(B3) an A-coring structure
 $\left ({\mathcal H},\Delta ,\varepsilon \right )$
on the A-bimodule
$\left ({\mathcal H},\Delta ,\varepsilon \right )$
on the A-bimodule
 ${}_{A^{\mathrm {e}}}{\mathcal H}={}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
, that is to say,
${}_{A^{\mathrm {e}}}{\mathcal H}={}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
, that is to say,  $$ \begin{align*} \Delta \colon {}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}} \to {}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}}\otimes_{A}{}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}} \qquad \text{and} \qquad \varepsilon\colon {}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}} \to A \end{align*} $$
$$ \begin{align*} \Delta \colon {}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}} \to {}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}}\otimes_{A}{}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}} \qquad \text{and} \qquad \varepsilon\colon {}_{s} {{\mathcal H}}{}_{t^{\mathrm{o}}} \to A \end{align*} $$
A-bilinear maps such that
(2.6) $$ \begin{align} \left(\Delta \otimes_{A} {\mathcal H}\right)\circ \Delta = \left({\mathcal H} \otimes_{A}\Delta\right) \circ \Delta \quad \text{and} \quad \left(\varepsilon\otimes_{A}{\mathcal H}\right)\circ \Delta = \operatorname{Id}_{\mathcal H} = \left({\mathcal H}\otimes_{A}\varepsilon\right)\circ \Delta; \end{align} $$
$$ \begin{align} \left(\Delta \otimes_{A} {\mathcal H}\right)\circ \Delta = \left({\mathcal H} \otimes_{A}\Delta\right) \circ \Delta \quad \text{and} \quad \left(\varepsilon\otimes_{A}{\mathcal H}\right)\circ \Delta = \operatorname{Id}_{\mathcal H} = \left({\mathcal H}\otimes_{A}\varepsilon\right)\circ \Delta; \end{align} $$
subject to the following compatibility conditions:
-
(B4)
 $\Delta $
takes values into
$\Delta $
takes values into
 ${}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}} \times _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
and
${}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}} \times _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
and
 $\Delta \colon {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}} \to {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}\times _{A}{}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
is a morphism of
$\Delta \colon {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}} \to {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}\times _{A}{}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
is a morphism of
 $\Bbbk $
-algebras;
$\Bbbk $
-algebras; -
(B5)
 $\varepsilon \Big (xs\big (\varepsilon \left (y\right )\big )\Big ) = \varepsilon \left (xy\right ) = \varepsilon \Big (xt\big (\varepsilon \left (y\right )^{\mathrm {o}}\big )\Big )$
for all
$\varepsilon \Big (xs\big (\varepsilon \left (y\right )\big )\Big ) = \varepsilon \left (xy\right ) = \varepsilon \Big (xt\big (\varepsilon \left (y\right )^{\mathrm {o}}\big )\Big )$
for all
 $x,y\in {\mathcal H}$
;
$x,y\in {\mathcal H}$
; -
(B6)
 $\varepsilon (1_{\mathcal H})=1_A$
.
$\varepsilon (1_{\mathcal H})=1_A$
.
A
![]() $\Bbbk $
-linear map
$\Bbbk $
-linear map
![]() $\varepsilon \colon {\mathcal H} \to A$
which is left
$\varepsilon \colon {\mathcal H} \to A$
which is left
![]() $A^{\mathrm {e}}$
-linear and satisfies (B5) and (B6) is called a left character on the
$A^{\mathrm {e}}$
-linear and satisfies (B5) and (B6) is called a left character on the
![]() $A^{\mathrm {e}}$
-ring
$A^{\mathrm {e}}$
-ring
![]() ${\mathcal H}$
(see [Reference Böhm3, Lemma 2.5 and following]).
${\mathcal H}$
(see [Reference Böhm3, Lemma 2.5 and following]).
A morphism of bialgebroids
![]() $\boldsymbol {\phi }\colon (A,{\mathcal H}) \to (B,{\mathcal K})$
is a pair of algebra maps
$\boldsymbol {\phi }\colon (A,{\mathcal H}) \to (B,{\mathcal K})$
is a pair of algebra maps
![]() $\left ( \phi _{{0}} \colon A \to B,\phi _{{1}} \colon {\mathcal H} \to {\mathcal K}\right )$
such that
$\left ( \phi _{{0}} \colon A \to B,\phi _{{1}} \colon {\mathcal H} \to {\mathcal K}\right )$
such that
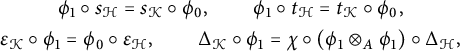 $$ \begin{gather*} \phi _{1}\circ s_{\mathcal H} = s_{\mathcal K} \circ \phi _{0}, \qquad \phi _{1}\circ t_{\mathcal H} = t_{\mathcal K} \circ \phi_{0}, \\ \varepsilon_{\mathcal K} \circ \phi _{1} = \phi _{0} \circ \varepsilon_{\mathcal H} , \qquad \Delta_{\mathcal K} \circ \phi _{1} =\chi \circ \left( \phi _{1}\otimes _{A}\phi_{1}\right) \circ \Delta_{\mathcal H}, \end{gather*} $$
$$ \begin{gather*} \phi _{1}\circ s_{\mathcal H} = s_{\mathcal K} \circ \phi _{0}, \qquad \phi _{1}\circ t_{\mathcal H} = t_{\mathcal K} \circ \phi_{0}, \\ \varepsilon_{\mathcal K} \circ \phi _{1} = \phi _{0} \circ \varepsilon_{\mathcal H} , \qquad \Delta_{\mathcal K} \circ \phi _{1} =\chi \circ \left( \phi _{1}\otimes _{A}\phi_{1}\right) \circ \Delta_{\mathcal H}, \end{gather*} $$
where
![]() $\chi \colon {\mathcal K} \otimes _{A} {\mathcal K} \rightarrow {\mathcal K} \otimes _{B} {\mathcal K}$
is the obvious projection induced by
$\chi \colon {\mathcal K} \otimes _{A} {\mathcal K} \rightarrow {\mathcal K} \otimes _{B} {\mathcal K}$
is the obvious projection induced by
![]() $\phi _0$
, that is,
$\phi _0$
, that is,
![]() $\chi \left (h\otimes _{A}k\right ) =h\otimes _{B}k$
. If
$\chi \left (h\otimes _{A}k\right ) =h\otimes _{B}k$
. If
![]() $A = B$
and
$A = B$
and
![]() $\phi _0 = \operatorname {Id}_A$
, then we say that
$\phi _0 = \operatorname {Id}_A$
, then we say that
![]() $\phi _1 : {\mathcal H} \to {\mathcal K}$
is a morphism of bialgebroids over A.
$\phi _1 : {\mathcal H} \to {\mathcal K}$
is a morphism of bialgebroids over A.
As a matter of terminology, a bialgebroid
![]() $(A,{\mathcal H})$
as in Definition 2.1 is often referred to as a left bialgebroid
$(A,{\mathcal H})$
as in Definition 2.1 is often referred to as a left bialgebroid
![]() ${\mathcal H}$
over A. Since in the following we will mainly deal with bialgebroids over a fixed base A, we may often omit to specify it and simply refer to
${\mathcal H}$
over A. Since in the following we will mainly deal with bialgebroids over a fixed base A, we may often omit to specify it and simply refer to
![]() $(A,{\mathcal H})$
as the left bialgebroid
$(A,{\mathcal H})$
as the left bialgebroid
![]() ${\mathcal H}$
.
${\mathcal H}$
.
Remark 2.6 Let us make explicit some of the relations involved in the definition of a left bialgebroid and some of their consequences. In terms of elements of A and
![]() ${\mathcal H}$
, and by resorting to Heyneman–Sweedler Sigma Notation, relation (2.6) becomes
${\mathcal H}$
, and by resorting to Heyneman–Sweedler Sigma Notation, relation (2.6) becomes
for all
![]() $x\in {\mathcal H}$
. The A-bilinearity of
$x\in {\mathcal H}$
. The A-bilinearity of
![]() $\Delta $
forces
$\Delta $
forces
for all
![]() $a\in A$
, and its multiplicativity forces, as a consequence,
$a\in A$
, and its multiplicativity forces, as a consequence,
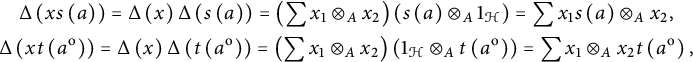 $$ \begin{gather*} \Delta\left(xs\left(a\right)\right) = \Delta\left(x\right)\Delta\left(s\left(a\right)\right) = \left(\sum x_1\otimes_{A}x_2\right)\left(s\left(a\right)\otimes_{A}1_{\mathcal H}\right) = \sum x_1s\left(a\right)\otimes_{A}x_2, \\ \Delta\left(xt\left(a^{\mathrm{o}}\right)\right) = \Delta\left(x\right)\Delta\left(t\left(a^{\mathrm{o}}\right)\right) = \left(\sum x_1\otimes_{A}x_2\right)\left(1_{\mathcal H}\otimes_{A}t\left(a^{\mathrm{o}}\right)\right) = \sum x_1\otimes_{A}x_2t\left(a^{\mathrm{o}}\right), \end{gather*} $$
$$ \begin{gather*} \Delta\left(xs\left(a\right)\right) = \Delta\left(x\right)\Delta\left(s\left(a\right)\right) = \left(\sum x_1\otimes_{A}x_2\right)\left(s\left(a\right)\otimes_{A}1_{\mathcal H}\right) = \sum x_1s\left(a\right)\otimes_{A}x_2, \\ \Delta\left(xt\left(a^{\mathrm{o}}\right)\right) = \Delta\left(x\right)\Delta\left(t\left(a^{\mathrm{o}}\right)\right) = \left(\sum x_1\otimes_{A}x_2\right)\left(1_{\mathcal H}\otimes_{A}t\left(a^{\mathrm{o}}\right)\right) = \sum x_1\otimes_{A}x_2t\left(a^{\mathrm{o}}\right), \end{gather*} $$
for all
![]() $x\in {\mathcal H}$
. In particular,
$x\in {\mathcal H}$
. In particular,
![]() $\Delta :{\mathcal H} \to {\mathcal H} \times _{A} {\mathcal H}$
is a morphism of
$\Delta :{\mathcal H} \to {\mathcal H} \times _{A} {\mathcal H}$
is a morphism of
![]() $A^{\mathrm {e}}$
-rings.
$A^{\mathrm {e}}$
-rings.
The following result is extremely well known (it underlies the monoidality of the category of left
![]() ${\mathcal H}$
-modules).
${\mathcal H}$
-modules).
Proposition 2.7 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid, and let
$(A,{\mathcal H})$
be a left bialgebroid, and let
![]() $M,N$
be two left
$M,N$
be two left
![]() ${\mathcal H}$
-modules. If we consider M and N as A-bimodules (left
${\mathcal H}$
-modules. If we consider M and N as A-bimodules (left
![]() $A^{\mathrm {e}}$
-modules) via the restriction of scalars along
$A^{\mathrm {e}}$
-modules) via the restriction of scalars along
![]() , then
, then
![]() $M \otimes _{A} N$
is a left
$M \otimes _{A} N$
is a left
![]() ${\mathcal H}\times _{A}{\mathcal H}$
-module with
${\mathcal H}\times _{A}{\mathcal H}$
-module with

Moreover, (2.8) is a morphism of
![]() $A^{\mathrm {e}} $
-bimodules if we consider
$A^{\mathrm {e}} $
-bimodules if we consider
![]() ${\mathcal H} \times _{A} {\mathcal H}$
endowed with the actions (2.4) from the left and (2.5) from the right and we consider
${\mathcal H} \times _{A} {\mathcal H}$
endowed with the actions (2.4) from the left and (2.5) from the right and we consider
![]() $\operatorname {End}_{\Bbbk }\left (M \otimes _{A} N\right )$
endowed with the left
$\operatorname {End}_{\Bbbk }\left (M \otimes _{A} N\right )$
endowed with the left
![]() $A^{\mathrm {e}} $
-action coming from the regular A-bimodule structure on the codomain and the right
$A^{\mathrm {e}} $
-action coming from the regular A-bimodule structure on the codomain and the right
![]() $A^{\mathrm {e}} $
-action coming from the regular A-bimodule structure on the domain. Equivalently,
$A^{\mathrm {e}} $
-action coming from the regular A-bimodule structure on the domain. Equivalently,
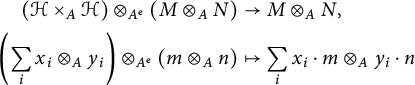 $$ \begin{align*}({\mathcal H} \times_{A} {\mathcal H})\otimes_{A^{\mathrm{e}} } (M \otimes_{A} N) & \to M \otimes_{A} N, \\ \left(\sum_ix_i \otimes_{A} y_i\right) \otimes_{A^{\mathrm{e}} } \left(m \otimes_{A} n\right) & \mapsto \sum_ix_i\cdot m\otimes_{A}y_i\cdot n\end{align*} $$
$$ \begin{align*}({\mathcal H} \times_{A} {\mathcal H})\otimes_{A^{\mathrm{e}} } (M \otimes_{A} N) & \to M \otimes_{A} N, \\ \left(\sum_ix_i \otimes_{A} y_i\right) \otimes_{A^{\mathrm{e}} } \left(m \otimes_{A} n\right) & \mapsto \sum_ix_i\cdot m\otimes_{A}y_i\cdot n\end{align*} $$
is a left
![]() $A^{\mathrm {e}} $
-linear action.
$A^{\mathrm {e}} $
-linear action.
Corollary 2.8 If
![]() $M,N$
are left
$M,N$
are left
![]() ${\mathcal H}$
-modules, then
${\mathcal H}$
-modules, then
![]() $M \otimes _{A} N$
is a left
$M \otimes _{A} N$
is a left
![]() ${\mathcal H}$
-module via restrictions of scalars along
${\mathcal H}$
-module via restrictions of scalars along
![]() $\Delta $
:
$\Delta $
:
and the latter is of
![]() $A^{\mathrm {e}} $
-bimodules. Equivalently,
$A^{\mathrm {e}} $
-bimodules. Equivalently,
is a left
![]() $A^{\mathrm {e}} $
-linear action. In particular, the category of left
$A^{\mathrm {e}} $
-linear action. In particular, the category of left
![]() ${\mathcal H}$
-modules is monoidal with tensor product
${\mathcal H}$
-modules is monoidal with tensor product
![]() $\otimes _{A}$
and unit object A. The left
$\otimes _{A}$
and unit object A. The left
![]() ${\mathcal H}$
-action on A is given by
${\mathcal H}$
-action on A is given by
for all
![]() $a \in A$
,
$a \in A$
,
![]() $h \in {\mathcal H}$
.
$h \in {\mathcal H}$
.
Definition 2.2 Given a left bialgebroid
![]() $(A,{\mathcal H})$
, a left
$(A,{\mathcal H})$
, a left
![]() ${\mathcal H}$
-module coring is a comonoid in the monoidal category
${\mathcal H}$
-module coring is a comonoid in the monoidal category
![]() $\big ({}_{{\mathcal H}}\textsf {Mod},\otimes _{A},A\big )$
of left
$\big ({}_{{\mathcal H}}\textsf {Mod},\otimes _{A},A\big )$
of left
![]() ${\mathcal H}$
-modules.
${\mathcal H}$
-modules.
2.5 Module corings and relative Hopf modules
Let
![]() $(A,{\mathcal H})$
be a left bialgebroid, and let
$(A,{\mathcal H})$
be a left bialgebroid, and let
![]() $\left (\overline {{\mathcal H}},\overline {\Delta },\overline {\varepsilon }\right )$
be a left
$\left (\overline {{\mathcal H}},\overline {\Delta },\overline {\varepsilon }\right )$
be a left
![]() ${\mathcal H}$
-module coring. Being an
${\mathcal H}$
-module coring. Being an
![]() ${\mathcal H}$
-module,
${\mathcal H}$
-module,
![]() $\overline {{\mathcal H}}$
has an A-bimodule structure
$\overline {{\mathcal H}}$
has an A-bimodule structure
![]() ${}_{s} {\overline {{\mathcal H}}}{}_{t^{\mathrm {o}}}$
given by
${}_{s} {\overline {{\mathcal H}}}{}_{t^{\mathrm {o}}}$
given by
for all
![]() $a,b \in A$
,
$a,b \in A$
,
![]() $u \in \overline {{\mathcal H}}$
, with respect to which it is an A-coring. In this setting, we may consider the category
$u \in \overline {{\mathcal H}}$
, with respect to which it is an A-coring. In this setting, we may consider the category
of relative
![]() $\Big (\overline {{\mathcal H}},{\mathcal H}\Big )$
-Hopf modules: these are left comodules over the comonoid
$\Big (\overline {{\mathcal H}},{\mathcal H}\Big )$
-Hopf modules: these are left comodules over the comonoid
![]() $\overline {{\mathcal H}}$
in the monoidal category
$\overline {{\mathcal H}}$
in the monoidal category
![]() $\left ({}_{{\mathcal H}}\textsf {Mod},\otimes _{A},A\right )$
. In details, they are left
$\left ({}_{{\mathcal H}}\textsf {Mod},\otimes _{A},A\right )$
. In details, they are left
![]() ${\mathcal H}$
-modules
${\mathcal H}$
-modules
![]() $(M,\mu _M\colon {\mathcal H} \otimes M \to M)$
together with a coassociative and counital left
$(M,\mu _M\colon {\mathcal H} \otimes M \to M)$
together with a coassociative and counital left
![]() $\overline {{\mathcal H}}$
-coaction
$\overline {{\mathcal H}}$
-coaction
which is also a morphism of left
![]() ${\mathcal H}$
-modules, that is, for all
${\mathcal H}$
-modules, that is, for all
![]() $h \in {\mathcal H}$
,
$h \in {\mathcal H}$
,
![]() $m \in M$
, one has
$m \in M$
, one has
In the present subsection, we are interested in the category
. A Hopf algebroid analog of Doi’s equivalence theorem [Reference Doi11, Theorem 2.3] will be of key importance in proving Theorem 3.14.
Now, suppose that
![]() $\pi \colon {\mathcal H} \to \overline {{\mathcal H}}$
is a morphism of left
$\pi \colon {\mathcal H} \to \overline {{\mathcal H}}$
is a morphism of left
![]() ${\mathcal H}$
-module corings. Recall that if C is an A-coring with distinguished group-like element
${\mathcal H}$
-module corings. Recall that if C is an A-coring with distinguished group-like element
![]() $g\in C$
and if
$g\in C$
and if
![]() $(N,\partial _N)$
is a left C-comodule, then
$(N,\partial _N)$
is a left C-comodule, then
is the so-called space of (left) coinvariant elements in N. In the standing hypotheses,
![]() $\pi (1_{\mathcal H})$
is a distinguished group-like element in
$\pi (1_{\mathcal H})$
is a distinguished group-like element in
![]() $\overline {{\mathcal H}}$
and we may consider
$\overline {{\mathcal H}}$
and we may consider
(also denoted by
![]() ${{\mathcal H}}^{\textsf {co}{\pi }}$
), which is the space of (left) coinvariant elements in
${{\mathcal H}}^{\textsf {co}{\pi }}$
), which is the space of (left) coinvariant elements in
![]() ${\mathcal H}$
under the (left)
${\mathcal H}$
under the (left)
![]() $\overline {{\mathcal H}}$
-coaction
$\overline {{\mathcal H}}$
-coaction
![]() ${\mathcal H} \to \overline {{\mathcal H}} \otimes _{A} {\mathcal H}$
given by
${\mathcal H} \to \overline {{\mathcal H}} \otimes _{A} {\mathcal H}$
given by
Remark 2.9 Observe that, in general,
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is just a right A-submodule (left
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is just a right A-submodule (left
![]() $A^{\mathrm {o}}$
-submodule) with respect to the action
$A^{\mathrm {o}}$
-submodule) with respect to the action
![]() $\triangleleft $
from (2.1) and a left A-submodule (right
$\triangleleft $
from (2.1) and a left A-submodule (right
![]() $A^{\mathrm {o}}$
-submodule) with respect to the action
$A^{\mathrm {o}}$
-submodule) with respect to the action
, because of (2.7):
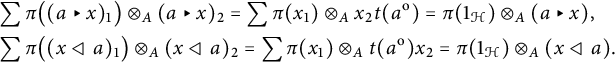
▲
Lemma 2.10 The space
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is an
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is an
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t, and
${\mathcal H}$
via t, and
![]() $\partial $
from (2.11) is right
$\partial $
from (2.11) is right
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
-linear.
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
-linear.
Proof Since
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}\subseteq {\mathcal H}$
and clearly
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}\subseteq {\mathcal H}$
and clearly
![]() $1_{{\mathcal H}} \in {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, to check that it is a
$1_{{\mathcal H}} \in {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, to check that it is a
![]() $\Bbbk $
-subalgebra, we just need to verify that the induced multiplication is well defined. To this aim, observe that
$\Bbbk $
-subalgebra, we just need to verify that the induced multiplication is well defined. To this aim, observe that
![]() $\overline {{\mathcal H}}\otimes _{A}{\mathcal H}$
has a left
$\overline {{\mathcal H}}\otimes _{A}{\mathcal H}$
has a left
![]() ${\mathcal H}$
-module structure given by Corollary 2.8 and it has a natural right
${\mathcal H}$
-module structure given by Corollary 2.8 and it has a natural right
![]() ${\mathcal H}$
-module structure given by
${\mathcal H}$
-module structure given by
Thanks to this, we may compute directly that for
![]() $x,y\in {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}},$
$x,y\in {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}},$
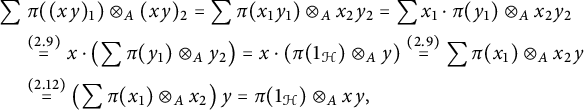 $$ \begin{align*} \sum & ~\pi((xy)_1) \otimes_{A} (xy)_2 = \sum \pi(x_1y_1) \otimes_{A} x_2y_2 = \sum x_1\cdot \pi(y_1) \otimes_{A} x_2y_2 \\ & \stackrel{(2.9)}{=} x \cdot \left(\sum \pi(y_1) \otimes_{A} y_2\right) = x\cdot \left( \pi(1_{\mathcal H}) \otimes_{A} y \right) \stackrel{(2.9)}{=} \sum \pi(x_1) \otimes_{A} x_2y \\ & \stackrel{(2.12)}{=} \left(\sum \pi(x_1) \otimes_{A} x_2\right)y = \pi(1_{\mathcal H}) \otimes_{A} xy, \end{align*} $$
$$ \begin{align*} \sum & ~\pi((xy)_1) \otimes_{A} (xy)_2 = \sum \pi(x_1y_1) \otimes_{A} x_2y_2 = \sum x_1\cdot \pi(y_1) \otimes_{A} x_2y_2 \\ & \stackrel{(2.9)}{=} x \cdot \left(\sum \pi(y_1) \otimes_{A} y_2\right) = x\cdot \left( \pi(1_{\mathcal H}) \otimes_{A} y \right) \stackrel{(2.9)}{=} \sum \pi(x_1) \otimes_{A} x_2y \\ & \stackrel{(2.12)}{=} \left(\sum \pi(x_1) \otimes_{A} x_2\right)y = \pi(1_{\mathcal H}) \otimes_{A} xy, \end{align*} $$
so that
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is indeed a subalgebra. Moreover, since
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is indeed a subalgebra. Moreover, since
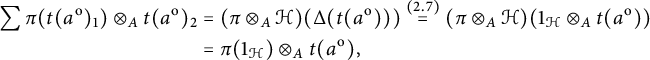 $$ \begin{align*} \sum \pi(t(a^{\mathrm{o}})_1) \otimes_{A} t(a^{\mathrm{o}})_2 & = (\pi \otimes_{A}{\mathcal H})(\Delta(t(a^{\mathrm{o}}))) \stackrel{(2.7)}{=} (\pi \otimes_{A}{\mathcal H})(1_{\mathcal H}\otimes_{A}t(a^{\mathrm{o}})) \\ & = \pi(1_{\mathcal H})\otimes_{A}t(a^{\mathrm{o}}), \end{align*} $$
$$ \begin{align*} \sum \pi(t(a^{\mathrm{o}})_1) \otimes_{A} t(a^{\mathrm{o}})_2 & = (\pi \otimes_{A}{\mathcal H})(\Delta(t(a^{\mathrm{o}}))) \stackrel{(2.7)}{=} (\pi \otimes_{A}{\mathcal H})(1_{\mathcal H}\otimes_{A}t(a^{\mathrm{o}})) \\ & = \pi(1_{\mathcal H})\otimes_{A}t(a^{\mathrm{o}}), \end{align*} $$
for all
![]() $a\in A$
, t takes values in
$a\in A$
, t takes values in
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
and so
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
and so
![]() ${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is
${{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
is
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t.
${\mathcal H}$
via t.
To conclude, notice that if
![]() $x \in {\mathcal H}$
and
$x \in {\mathcal H}$
and
![]() $b \in {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, then
$b \in {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, then
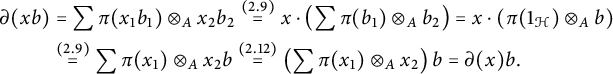 $$ \begin{align*} \partial(xb) & = \sum \pi(x_1b_1) \otimes_{A} x_2b_2 \stackrel{(2.9)}{=} x \cdot \left(\sum \pi(b_1) \otimes_{A} b_2\right) = x\cdot \left( \pi(1_{\mathcal H}) \otimes_{A} b \right) \\ & \stackrel{(2.9)}{=} \sum \pi(x_1) \otimes_{A} x_2b \stackrel{(2.12)}{=} \left(\sum \pi(x_1) \otimes_{A} x_2\right)b = \partial(x)b.\\[-37pt] \end{align*} $$
$$ \begin{align*} \partial(xb) & = \sum \pi(x_1b_1) \otimes_{A} x_2b_2 \stackrel{(2.9)}{=} x \cdot \left(\sum \pi(b_1) \otimes_{A} b_2\right) = x\cdot \left( \pi(1_{\mathcal H}) \otimes_{A} b \right) \\ & \stackrel{(2.9)}{=} \sum \pi(x_1) \otimes_{A} x_2b \stackrel{(2.12)}{=} \left(\sum \pi(x_1) \otimes_{A} x_2\right)b = \partial(x)b.\\[-37pt] \end{align*} $$
Set
, for the sake of brevity. Since
![]() ${\mathcal H}$
becomes a right B-module by restriction of scalars along
${\mathcal H}$
becomes a right B-module by restriction of scalars along
![]() $\iota : B \to {\mathcal H}$
, we can consider the category
$\iota : B \to {\mathcal H}$
, we can consider the category
![]() ${}_{B}\textsf {Mod}$
and the extension of scalars functor
${}_{B}\textsf {Mod}$
and the extension of scalars functor
which is left adjoint to the restriction of scalars functor
![]() ${_{\iota }\big (-\big )} \colon {}_{{\mathcal H}}\textsf {Mod} \to {}_{B}\textsf {Mod}.$
It turns out that the natural transformation
${_{\iota }\big (-\big )} \colon {}_{{\mathcal H}}\textsf {Mod} \to {}_{B}\textsf {Mod}.$
It turns out that the natural transformation
induces a morphism of comonads
as in [Reference Gómez-Torrecillas21, Proposition 2.1] and so, since
![]() is also the category of Eilenberg–Moore objects for the comonad
is also the category of Eilenberg–Moore objects for the comonad
![]() $\overline {{\mathcal H}} \otimes _{A} -$
over
$\overline {{\mathcal H}} \otimes _{A} -$
over
![]() ${}_{{\mathcal H}}\textsf {Mod}$
, the functor F induces a functor
${}_{{\mathcal H}}\textsf {Mod}$
, the functor F induces a functor
![]() . The following theorem is nothing else than [Reference Gómez-Torrecillas21, Theorem 2.7].
. The following theorem is nothing else than [Reference Gómez-Torrecillas21, Theorem 2.7].
Theorem 2.11 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid with
$(A,{\mathcal H})$
be a left bialgebroid with
![]() ${}_{s} {{{\mathcal H}}} \ A$
-flat. If
${}_{s} {{{\mathcal H}}} \ A$
-flat. If
![]() $\overline {{\mathcal H}}$
is a left
$\overline {{\mathcal H}}$
is a left
![]() ${\mathcal H}$
-module coring together with a morphism
${\mathcal H}$
-module coring together with a morphism
![]() $\pi \colon {\mathcal H} \to \overline {{\mathcal H}}$
of left
$\pi \colon {\mathcal H} \to \overline {{\mathcal H}}$
of left
![]() ${\mathcal H}$
-module corings and if
${\mathcal H}$
-module corings and if
![]() $B = {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, then
$B = {{\mathcal H}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, then
is an equivalence of categories if and only if:
-
(1)
 ${\mathcal H} \otimes _{B} - \colon {}_{B}\textsf {Mod} \to {}_{{\mathcal H}}\textsf {Mod}$
is comonadic and
${\mathcal H} \otimes _{B} - \colon {}_{B}\textsf {Mod} \to {}_{{\mathcal H}}\textsf {Mod}$
is comonadic and -
(2) the canonical morphism of comonads
 $\Theta $
is a natural isomorphism.
$\Theta $
is a natural isomorphism.
Lemma 2.12 The natural transformation
![]() $\Theta $
of (2.13) is a natural isomorphism if and only if
$\Theta $
of (2.13) is a natural isomorphism if and only if
is an isomorphism.
Proof If
![]() $\Theta $
is a natural isomorphism, then
$\Theta $
is a natural isomorphism, then
![]() $\Theta _{{\mathcal H}} = \xi $
is an isomorphism. Conversely, since
$\Theta _{{\mathcal H}} = \xi $
is an isomorphism. Conversely, since
![]() $\xi $
is right
$\xi $
is right
![]() ${\mathcal H}$
-linear with respect to the regular right
${\mathcal H}$
-linear with respect to the regular right
![]() ${\mathcal H}$
-module structures, we may conclude that if
${\mathcal H}$
-module structures, we may conclude that if
![]() $\xi $
is an isomorphism, then
$\xi $
is an isomorphism, then
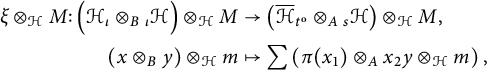 $$ \begin{align*} \xi \otimes_{{\mathcal H}} M \colon \Big({\mathcal H}_{\iota} \otimes_{B} {{}_{\iota}{\mathcal H}}\Big) \otimes_{{\mathcal H}} M & \to \left({\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}}\right)\otimes_{{\mathcal H}} M, \\ \left(x \otimes_{B} y\right)\otimes_{{\mathcal H}}m & \mapsto \sum \left(\pi(x_1) \otimes_{A} x_2y \otimes_{{\mathcal H}} m\right), \end{align*} $$
$$ \begin{align*} \xi \otimes_{{\mathcal H}} M \colon \Big({\mathcal H}_{\iota} \otimes_{B} {{}_{\iota}{\mathcal H}}\Big) \otimes_{{\mathcal H}} M & \to \left({\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}}\right)\otimes_{{\mathcal H}} M, \\ \left(x \otimes_{B} y\right)\otimes_{{\mathcal H}}m & \mapsto \sum \left(\pi(x_1) \otimes_{A} x_2y \otimes_{{\mathcal H}} m\right), \end{align*} $$
is an isomorphism for every M in
![]() ${}_{{\mathcal H}}\textsf {Mod}$
, natural in M. The commutativity of the diagram
${}_{{\mathcal H}}\textsf {Mod}$
, natural in M. The commutativity of the diagram
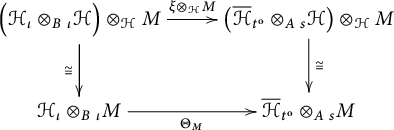
allows us to conclude that if
![]() $\xi $
is an isomorphism, then
$\xi $
is an isomorphism, then
![]() $\Theta $
is a natural isomorphism. Notice that, due to the fact that only regular module structures are involved, the vertical isomorphisms are, in fact, the canonical isomorphism
$\Theta $
is a natural isomorphism. Notice that, due to the fact that only regular module structures are involved, the vertical isomorphisms are, in fact, the canonical isomorphism
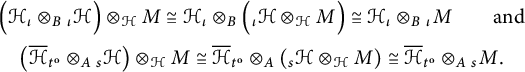 $$ \begin{gather*} \Big({\mathcal H}_{\iota} \otimes_{B} {{}_{\iota}{\mathcal H}}\Big) \otimes_{{\mathcal H}} M \cong {\mathcal H}_{\iota} \otimes_{B} \Big({{}_{\iota}{\mathcal H}} \otimes_{{\mathcal H}} M\Big) \cong {\mathcal H}_{\iota} \otimes_{B} {{}_{\iota} M} \qquad \text{and} \\ \left({\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}}\right)\otimes_{{\mathcal H}} M \cong {\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} \left({}_{s} {{{\mathcal H}}}\otimes_{{\mathcal H}} M\right) \cong {\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{M}}. \\[-35pt] \end{gather*} $$
$$ \begin{gather*} \Big({\mathcal H}_{\iota} \otimes_{B} {{}_{\iota}{\mathcal H}}\Big) \otimes_{{\mathcal H}} M \cong {\mathcal H}_{\iota} \otimes_{B} \Big({{}_{\iota}{\mathcal H}} \otimes_{{\mathcal H}} M\Big) \cong {\mathcal H}_{\iota} \otimes_{B} {{}_{\iota} M} \qquad \text{and} \\ \left({\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}}\right)\otimes_{{\mathcal H}} M \cong {\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} \left({}_{s} {{{\mathcal H}}}\otimes_{{\mathcal H}} M\right) \cong {\overline{{\mathcal H}}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{M}}. \\[-35pt] \end{gather*} $$
In general, even when
![]() ${\mathcal K}$
is not an equivalence of categories,
${\mathcal K}$
is not an equivalence of categories,
![]() ${\mathcal K}$
still admits a right adjoint functor, as in the case for ordinary Hopf algebras.
${\mathcal K}$
still admits a right adjoint functor, as in the case for ordinary Hopf algebras.
Proposition 2.13 The construction
![]() for every M in
for every M in
![]() induces a functor
induces a functor
![]() which is right adjoint to
which is right adjoint to
![]() ${\mathcal K}$
. Unit and counit are given by
${\mathcal K}$
. Unit and counit are given by
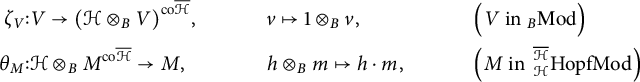
respectively.
Proof Given a relative Hopf module
![]() $(M,\mu _M,\partial _M)$
, denote by
$(M,\mu _M,\partial _M)$
, denote by
![]() $\Omega (M)$
its underlying H-module structure
$\Omega (M)$
its underlying H-module structure
![]() $(M,\mu _M)$
. In view of [Reference Gómez-Torrecillas21, Proposition 2.3],
$(M,\mu _M)$
. In view of [Reference Gómez-Torrecillas21, Proposition 2.3],
![]() ${\mathcal K}$
admits a right adjoint which is explicitly realized on objects as the equalizer of the parallel pair
${\mathcal K}$
admits a right adjoint which is explicitly realized on objects as the equalizer of the parallel pair
which is exactly
![]() ${M}^{\textsf {co}{\overline {{\mathcal H}}}}$
.
${M}^{\textsf {co}{\overline {{\mathcal H}}}}$
.
3 The correspondence for arbitrary Hopf Algebroids
This section contains our first main result, namely, Theorem 3.15.
3.1 The correspondence between left ideals two-sided coideals and right coideal subrings
Henceforth, all bialgebroids will be left ones.
3.1.1 General facts about left ideals two-sided coideals and right coideal subrings
As a matter of notation, for
![]() $(A,{\mathcal H})$
a bialgebroid and
$(A,{\mathcal H})$
a bialgebroid and
![]() $B\subseteq {\mathcal H}$
, we set
$B\subseteq {\mathcal H}$
, we set
Denote by
![]() $\iota \colon B \to {\mathcal H}$
the inclusion. Assume that B is an
$\iota \colon B \to {\mathcal H}$
the inclusion. Assume that B is an
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t (as we will have later in the paper), that is, B is an
${\mathcal H}$
via t (as we will have later in the paper), that is, B is an
![]() $A^{\mathrm {o}}$
-ring via a
$A^{\mathrm {o}}$
-ring via a
![]() $\Bbbk $
-algebra extension
$\Bbbk $
-algebra extension
![]() $t'\colon A^{\mathrm {o}}\to B$
such that
$t'\colon A^{\mathrm {o}}\to B$
such that
![]() $\iota \circ t'= t$
. If we consider the restriction
$\iota \circ t'= t$
. If we consider the restriction
of
![]() $\varepsilon $
to B, then the latter is a right A-linear morphism (left
$\varepsilon $
to B, then the latter is a right A-linear morphism (left
![]() $A^{\mathrm {o}}$
-linear, for the sake of precision) and
$A^{\mathrm {o}}$
-linear, for the sake of precision) and
![]() $B^+ = {\mathcal H}^+ \cap B = \ker (\varepsilon )\cap B = \ker (\varepsilon ')$
.
$B^+ = {\mathcal H}^+ \cap B = \ker (\varepsilon )\cap B = \ker (\varepsilon ')$
.
Remark 3.1 If B is an
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t, then we have that
${\mathcal H}$
via t, then we have that
is a short exact sequence of left B-modules, where A has the left B-module structure coming from the restriction of scalars along the inclusion
![]() $\iota $
of B into
$\iota $
of B into
![]() ${\mathcal H}$
. Namely,
${\mathcal H}$
. Namely,
for all
![]() $a\in A,b\in B$
(see (2.10)). Moreover, (3.1) is a split short exact sequence of right A-modules (in fact, left
$a\in A,b\in B$
(see (2.10)). Moreover, (3.1) is a split short exact sequence of right A-modules (in fact, left
![]() $A^{\mathrm {o}}$
-modules via
$A^{\mathrm {o}}$
-modules via
![]() $t'$
), where
$t'$
), where
![]() $t'$
provides an A-linear section for
$t'$
provides an A-linear section for
![]() $\varepsilon '$
in view of (B6):
$\varepsilon '$
in view of (B6):
Recall that an
![]() $A^{\mathrm {o}}$
-subring B of
$A^{\mathrm {o}}$
-subring B of
![]() ${\mathcal H}$
via t is a right
${\mathcal H}$
via t is a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring if it admits a right A-linear coaction
$A^{\mathrm {o}}$
-subring if it admits a right A-linear coaction
![]() $\delta \colon {B}{}_{t^{\mathrm {o}}} \to {B}{}_{t^{\mathrm {o}}} \otimes _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
such that the following diagram commutes:
$\delta \colon {B}{}_{t^{\mathrm {o}}} \to {B}{}_{t^{\mathrm {o}}} \otimes _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
such that the following diagram commutes:
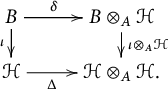
Remark 3.2 It is a well-known fact that if
![]() $(A,{\mathcal H})$
is a left bialgebroid, then the category
$(A,{\mathcal H})$
is a left bialgebroid, then the category
![]() $ {}^{{\mathcal H}}\textsf {Comod}$
of left
$ {}^{{\mathcal H}}\textsf {Comod}$
of left
![]() ${\mathcal H}$
-comodules is a monoidal category with tensor product
${\mathcal H}$
-comodules is a monoidal category with tensor product
![]() $\otimes _{A}$
and unit object A, where the
$\otimes _{A}$
and unit object A, where the
![]() ${\mathcal H}$
-coaction on A is provided by the source map (see, e.g., [Reference Böhm3, Theorem 3.18], where the property is stated for the right-hand scenario) and where every left
${\mathcal H}$
-coaction on A is provided by the source map (see, e.g., [Reference Böhm3, Theorem 3.18], where the property is stated for the right-hand scenario) and where every left
![]() ${\mathcal H}$
-comodule M is a right A-module with action
${\mathcal H}$
-comodule M is a right A-module with action
for all
![]() $m \in M$
and
$m \in M$
and
![]() $a \in A$
. By applying this result to the co-opposite left bialgebroid
$a \in A$
. By applying this result to the co-opposite left bialgebroid
![]() $(A^{\mathrm {o}},{\mathcal H}^{\mathrm {co}})$
, we conclude that the category
$(A^{\mathrm {o}},{\mathcal H}^{\mathrm {co}})$
, we conclude that the category
![]() $ \textsf {Comod}{}^{{\mathcal H}}$
of right comodules over the left bialgebroid
$ \textsf {Comod}{}^{{\mathcal H}}$
of right comodules over the left bialgebroid
![]() $(A,{\mathcal H})$
is monoidal too, with tensor product
$(A,{\mathcal H})$
is monoidal too, with tensor product
![]() $\otimes _{A^{\mathrm {o}}}$
and unit
$\otimes _{A^{\mathrm {o}}}$
and unit
![]() $A^{\mathrm {o}}$
, where the
$A^{\mathrm {o}}$
, where the
![]() ${\mathcal H}$
-coaction on
${\mathcal H}$
-coaction on
![]() $A^{\mathrm {o}}$
is provided by the target map. In this setting, if
$A^{\mathrm {o}}$
is provided by the target map. In this setting, if
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat, then a right
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat, then a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring is nothing other than a monoid in
$A^{\mathrm {o}}$
-subring is nothing other than a monoid in
![]() $\big ( \textsf {Comod}{}^{{\mathcal H}},\otimes _{A^{\mathrm {o}}},A^{\mathrm {o}}\big )$
.
$\big ( \textsf {Comod}{}^{{\mathcal H}},\otimes _{A^{\mathrm {o}}},A^{\mathrm {o}}\big )$
.
Recall that a two-sided coideal N in a bialgebroid
![]() $(A,{\mathcal H})$
is an A-subbimodule of
$(A,{\mathcal H})$
is an A-subbimodule of
![]() ${}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
such that
${}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
such that
where
![]() $\operatorname {Im}(-)$
denotes the canonical image in the tensor product
$\operatorname {Im}(-)$
denotes the canonical image in the tensor product
![]() ${}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}} \otimes _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
.
${}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}} \otimes _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
.
3.1.2 Correspondence between left ideals two-sided coideals and quotient module corings
Proposition 3.3 We have a well-defined bijective correspondence
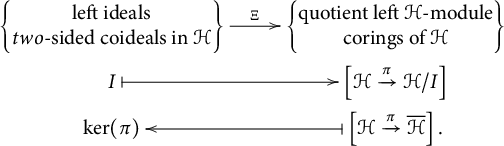
Proof Let us begin by picking a left ideal two-sided coideal
![]() $I\subseteq {\mathcal H}$
and consider the canonical projection
$I\subseteq {\mathcal H}$
and consider the canonical projection
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
. Since I is a left
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
. Since I is a left
![]() ${\mathcal H}$
-submodule of
${\mathcal H}$
-submodule of
![]() ${\mathcal H}$
,
${\mathcal H}$
,
![]() ${\mathcal H}/I$
becomes a left
${\mathcal H}/I$
becomes a left
![]() ${\mathcal H}$
-module and, in particular, an
${\mathcal H}$
-module and, in particular, an
![]() $A^{\mathrm {e}}$
-module with
$A^{\mathrm {e}}$
-module with
![]() ${}_{s} {{\mathcal H}/I}{}_{t^{\mathrm {o}}}$
and
${}_{s} {{\mathcal H}/I}{}_{t^{\mathrm {o}}}$
and
![]() $\pi $
is left
$\pi $
is left
![]() ${\mathcal H}$
-linear and, in particular, A-bilinear. Since I is a two-sided coideal,
${\mathcal H}$
-linear and, in particular, A-bilinear. Since I is a two-sided coideal,
![]() ${}_{s} {{\mathcal H}/I}{}_{t^{\mathrm {o}}}$
inherits a structure
${}_{s} {{\mathcal H}/I}{}_{t^{\mathrm {o}}}$
inherits a structure
![]() $\left (\overline {\Delta },\overline {\varepsilon }\right )$
of A-coring in such a way that
$\left (\overline {\Delta },\overline {\varepsilon }\right )$
of A-coring in such a way that
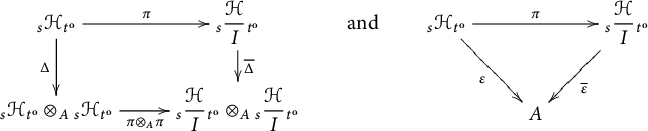
are commutative diagrams in
![]() ${}_{A}{\textsf {Mod}}_{A} = {}_{A^{\mathrm {e}}}\textsf {Mod}$
. Let us show that both
${}_{A}{\textsf {Mod}}_{A} = {}_{A^{\mathrm {e}}}\textsf {Mod}$
. Let us show that both
![]() $\overline {\Delta }$
and
$\overline {\Delta }$
and
![]() $\overline {\varepsilon }$
are morphisms of left
$\overline {\varepsilon }$
are morphisms of left
![]() ${\mathcal H}$
-modules. Set
${\mathcal H}$
-modules. Set
, for the sake of brevity. The left
![]() ${\mathcal H}$
-linearity of
${\mathcal H}$
-linearity of
![]() $\overline {\Delta }$
is provided by the commutativity of the following diagram:
$\overline {\Delta }$
is provided by the commutativity of the following diagram:
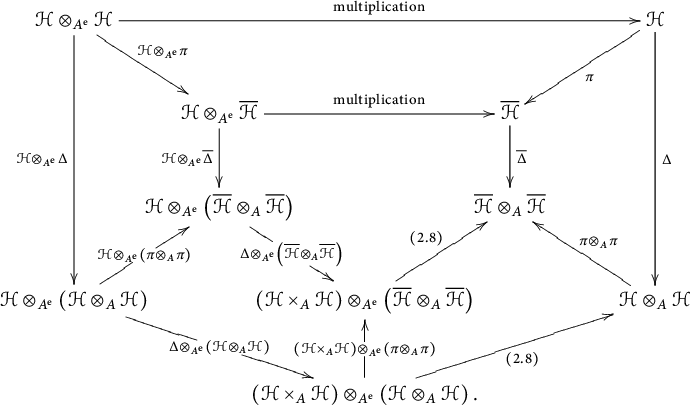
The left
![]() ${\mathcal H}$
-linearity of
${\mathcal H}$
-linearity of
![]() $\overline {\varepsilon }$
instead is provided by the commutativity of the following diagram:
$\overline {\varepsilon }$
instead is provided by the commutativity of the following diagram:
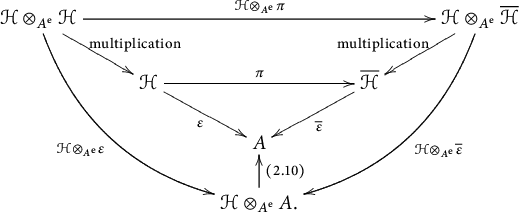
Summing up,
![]() ${\mathcal H}/I$
is a left
${\mathcal H}/I$
is a left
![]() ${\mathcal H}$
-module coring.
${\mathcal H}$
-module coring.
In the opposite direction, assume that we have a surjective morphism of vector spaces
![]() $\pi \colon {\mathcal H} \to \overline {{\mathcal H}}$
which is of left
$\pi \colon {\mathcal H} \to \overline {{\mathcal H}}$
which is of left
![]() ${\mathcal H}$
-module corings and consider
${\mathcal H}$
-module corings and consider
![]() $\ker (\pi ) \subseteq {\mathcal H}$
. Since
$\ker (\pi ) \subseteq {\mathcal H}$
. Since
![]() $\pi $
is of left
$\pi $
is of left
![]() ${\mathcal H}$
-modules,
${\mathcal H}$
-modules,
![]() $\ker (\pi )$
is a left ideal in
$\ker (\pi )$
is a left ideal in
![]() ${\mathcal H}$
. Moreover, being
${\mathcal H}$
. Moreover, being
![]() $\pi $
of A-corings, we have that the following diagram with exact rows commutes:
$\pi $
of A-corings, we have that the following diagram with exact rows commutes:
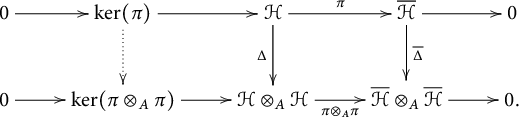
Since
![]() $\ker (\pi \otimes _{A} \pi ) = \operatorname {Im}\big (\ker (\pi ) \otimes _{A} {\mathcal H} + {\mathcal H} \otimes _{A} \ker (\pi )\big )$
and since
$\ker (\pi \otimes _{A} \pi ) = \operatorname {Im}\big (\ker (\pi ) \otimes _{A} {\mathcal H} + {\mathcal H} \otimes _{A} \ker (\pi )\big )$
and since
![]() $\varepsilon \big (\ker (\pi )\big ) \subseteq \overline {\varepsilon }\big (\pi \big (\ker (\pi )\big )\big ) = 0_A$
, it follows that
$\varepsilon \big (\ker (\pi )\big ) \subseteq \overline {\varepsilon }\big (\pi \big (\ker (\pi )\big )\big ) = 0_A$
, it follows that
![]() $\ker (\pi )$
is also a two-sided coideal.
$\ker (\pi )$
is also a two-sided coideal.
3.1.3 From left ideal two-sided coideals to right coideal subrings
Proposition 3.4 Under the assumption that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat, we have a well-defined inclusion-preserving correspondence
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat, we have a well-defined inclusion-preserving correspondence

Proof Let us begin by picking a left ideal two-sided coideal
![]() $I\subseteq {\mathcal H}$
, and consider the canonical projection
$I\subseteq {\mathcal H}$
, and consider the canonical projection
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
. We already know from Proposition 3.3 that
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
. We already know from Proposition 3.3 that
![]() ${\mathcal H}/I$
is an A-coring and that the canonical projection
${\mathcal H}/I$
is an A-coring and that the canonical projection
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
is a morphism of left
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
is a morphism of left
![]() ${\mathcal H}$
-module corings. Therefore, in view of Lemma 2.10,
${\mathcal H}$
-module corings. Therefore, in view of Lemma 2.10,
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
is an
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
is an
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t. To finish checking the validity of the first correspondence, we are left to check that it is an
${\mathcal H}$
via t. To finish checking the validity of the first correspondence, we are left to check that it is an
![]() ${\mathcal H}$
-comodule with respect to the obvious coaction induced by
${\mathcal H}$
-comodule with respect to the obvious coaction induced by
![]() $\Delta $
. To this aim, recall that
$\Delta $
. To this aim, recall that
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
can be realized as the following equalizer in
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
can be realized as the following equalizer in
![]() $\textsf {Mod}_{A}$
(in fact, in
$\textsf {Mod}_{A}$
(in fact, in
![]() ${}_{A^{\mathrm {o}}}\textsf {Mod}$
):
${}_{A^{\mathrm {o}}}\textsf {Mod}$
):
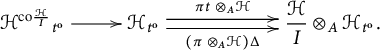
Since
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat, it is enough for us to check that, for every
${}_{s} {{{\mathcal H}}}$
is A-flat, it is enough for us to check that, for every
![]() $x\in {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
,
$x\in {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
,
![]() $\sum x_1 \otimes _{A} x_2$
equalizes the pair
$\sum x_1 \otimes _{A} x_2$
equalizes the pair
![]() $\Big ((\pi \circ t) \otimes _{A} {\mathcal H} \otimes _{A} {\mathcal H}, (\pi \otimes _{A}{\mathcal H}\otimes _{A}{\mathcal H})(\Delta \otimes _{A}{\mathcal H})\Big )$
. However,
$\Big ((\pi \circ t) \otimes _{A} {\mathcal H} \otimes _{A} {\mathcal H}, (\pi \otimes _{A}{\mathcal H}\otimes _{A}{\mathcal H})(\Delta \otimes _{A}{\mathcal H})\Big )$
. However,
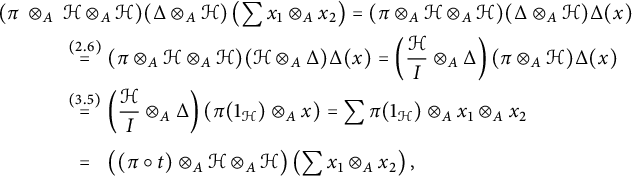 $$ \begin{align*} (\pi ~\otimes_{A}~ & {\mathcal H} \otimes_{A} {\mathcal H})(\Delta\otimes_{A}{\mathcal H})\left(\sum x_1 \otimes_{A} x_2\right) = (\pi\otimes_{A}{\mathcal H}\otimes_{A}{\mathcal H})(\Delta\otimes_{A}{\mathcal H})\Delta(x) \\ & \stackrel{(2.6)}{=} (\pi\otimes_{A}{\mathcal H}\otimes_{A}{\mathcal H})({\mathcal H}\otimes_{A}\Delta)\Delta(x) = \left(\frac{{\mathcal H}}{I}\otimes_{A}\Delta\right)(\pi\otimes_{A}{\mathcal H})\Delta(x) \\ & \stackrel{(3.5)}{=} \left(\frac{{\mathcal H}}{I}\otimes_{A}\Delta\right)(\pi(1_{\mathcal H})\otimes_{A}x) = \sum \pi(1_{\mathcal H}) \otimes_{A} x_1 \otimes_{A} x_2 \\ & \stackrel{\phantom{(2.6)}}{=} \big((\pi\circ t)\otimes_{A}{\mathcal H}\otimes_{A}{\mathcal H}\big)\left(\sum x_1\otimes_{A}x_2\right), \end{align*} $$
$$ \begin{align*} (\pi ~\otimes_{A}~ & {\mathcal H} \otimes_{A} {\mathcal H})(\Delta\otimes_{A}{\mathcal H})\left(\sum x_1 \otimes_{A} x_2\right) = (\pi\otimes_{A}{\mathcal H}\otimes_{A}{\mathcal H})(\Delta\otimes_{A}{\mathcal H})\Delta(x) \\ & \stackrel{(2.6)}{=} (\pi\otimes_{A}{\mathcal H}\otimes_{A}{\mathcal H})({\mathcal H}\otimes_{A}\Delta)\Delta(x) = \left(\frac{{\mathcal H}}{I}\otimes_{A}\Delta\right)(\pi\otimes_{A}{\mathcal H})\Delta(x) \\ & \stackrel{(3.5)}{=} \left(\frac{{\mathcal H}}{I}\otimes_{A}\Delta\right)(\pi(1_{\mathcal H})\otimes_{A}x) = \sum \pi(1_{\mathcal H}) \otimes_{A} x_1 \otimes_{A} x_2 \\ & \stackrel{\phantom{(2.6)}}{=} \big((\pi\circ t)\otimes_{A}{\mathcal H}\otimes_{A}{\mathcal H}\big)\left(\sum x_1\otimes_{A}x_2\right), \end{align*} $$
and hence
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
is indeed a right
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
is indeed a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring via t.
$A^{\mathrm {o}}$
-subring via t.
It is clear that the correspondence is inclusion-preserving because if
![]() $I \subseteq J$
, then we have a left
$I \subseteq J$
, then we have a left
![]() ${\mathcal H}$
-linear surjective morphism of A-corings
${\mathcal H}$
-linear surjective morphism of A-corings
![]() ${\mathcal H}/I \twoheadrightarrow {\mathcal H}/J$
and hence
${\mathcal H}/I \twoheadrightarrow {\mathcal H}/J$
and hence
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}} \subseteq {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{J}}}$
.
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}} \subseteq {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{J}}}$
.
3.1.4 From right coideal subrings to left ideals two-sided coideals
In this section, we consider a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring B of
$A^{\mathrm {o}}$
-subring B of
![]() ${\mathcal H}$
and utilize the notation introduced in Section 3.1.1.
${\mathcal H}$
and utilize the notation introduced in Section 3.1.1.
Lemma 3.5 Let B be a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t, and let
${\mathcal H}$
via t, and let
![]() $\iota \colon B \to {\mathcal H}$
be the inclusion. Denote by
$\iota \colon B \to {\mathcal H}$
be the inclusion. Denote by
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/{\mathcal H} B^+$
the canonical projection of left
$\pi \colon {\mathcal H} \to {\mathcal H}/{\mathcal H} B^+$
the canonical projection of left
![]() ${\mathcal H}$
-modules. Then
${\mathcal H}$
-modules. Then
In particular,
Proof Notice that for all
![]() $b \in B$
we have that
$b \in B$
we have that
![]() $b - t'\big (\varepsilon '(b)^{\mathrm {o}}\big ) \in B^+$
and hence
$b - t'\big (\varepsilon '(b)^{\mathrm {o}}\big ) \in B^+$
and hence
![]() ${\iota \Big (b - t'\big (\varepsilon '(b)^{\mathrm {o}}\big )\Big ) \in {\mathcal H} B^+}$
. Therefore,
${\iota \Big (b - t'\big (\varepsilon '(b)^{\mathrm {o}}\big )\Big ) \in {\mathcal H} B^+}$
. Therefore,
The right-most equality follows by definition of
![]() $t'$
and
$t'$
and
![]() $\varepsilon '$
. To conclude, observe that
$\varepsilon '$
. To conclude, observe that
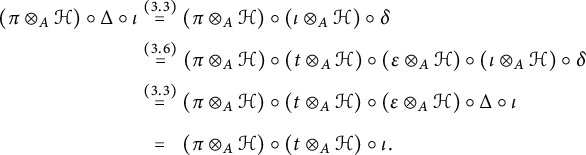 $$ \begin{align*} \left(\pi \otimes_{A} {\mathcal H}\right) \circ \Delta \circ \iota & \stackrel{(3.3)}{=} \left(\pi \otimes_{A} {\mathcal H}\right) \circ \left(\iota \otimes_{A} {\mathcal H}\right) \circ \delta \\ & \stackrel{(3.6)}{=} \left(\pi \otimes_{A} {\mathcal H}\right) \circ (t \otimes_{A} {\mathcal H}) \circ (\varepsilon \otimes_{A} {\mathcal H}) \circ \left(\iota \otimes_{A} {\mathcal H}\right) \circ \delta \\ & \stackrel{(3.3)}{=} \left(\pi \otimes_{A} {\mathcal H}\right) \circ (t \otimes_{A} {\mathcal H}) \circ (\varepsilon \otimes_{A} {\mathcal H}) \circ \Delta \circ \iota \\ & \stackrel{\phantom{(3.3)}}{=} (\pi \otimes_{A} {\mathcal H}) \circ (t \otimes_{A} {\mathcal H}) \circ \iota.\\[-38pt] \end{align*} $$
$$ \begin{align*} \left(\pi \otimes_{A} {\mathcal H}\right) \circ \Delta \circ \iota & \stackrel{(3.3)}{=} \left(\pi \otimes_{A} {\mathcal H}\right) \circ \left(\iota \otimes_{A} {\mathcal H}\right) \circ \delta \\ & \stackrel{(3.6)}{=} \left(\pi \otimes_{A} {\mathcal H}\right) \circ (t \otimes_{A} {\mathcal H}) \circ (\varepsilon \otimes_{A} {\mathcal H}) \circ \left(\iota \otimes_{A} {\mathcal H}\right) \circ \delta \\ & \stackrel{(3.3)}{=} \left(\pi \otimes_{A} {\mathcal H}\right) \circ (t \otimes_{A} {\mathcal H}) \circ (\varepsilon \otimes_{A} {\mathcal H}) \circ \Delta \circ \iota \\ & \stackrel{\phantom{(3.3)}}{=} (\pi \otimes_{A} {\mathcal H}) \circ (t \otimes_{A} {\mathcal H}) \circ \iota.\\[-38pt] \end{align*} $$
Proposition 3.6 We have a well-defined inclusion-preserving correspondence

Proof Assume that we have a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring B of
$A^{\mathrm {o}}$
-subring B of
![]() ${\mathcal H}$
, where the
${\mathcal H}$
, where the
![]() $A^{\mathrm {o}}$
-ring structure comes from a
$A^{\mathrm {o}}$
-ring structure comes from a
![]() $\Bbbk $
-algebra extension
$\Bbbk $
-algebra extension
![]() $t'\colon A^{\mathrm {o}}\to B$
as in Remark 3.1. We may tensor (3.1) by
$t'\colon A^{\mathrm {o}}\to B$
as in Remark 3.1. We may tensor (3.1) by
![]() ${\mathcal H}$
over B on the left and eventually apply the Snake Lemma to find the following commutative diagram of left
${\mathcal H}$
over B on the left and eventually apply the Snake Lemma to find the following commutative diagram of left
![]() ${\mathcal H}$
-modules, with exact rows:
${\mathcal H}$
-modules, with exact rows:

If we consider
![]() , then this is a left
, then this is a left
![]() ${\mathcal H}$
-ideal by construction. Let us prove that it is also a two-sided coideal.
${\mathcal H}$
-ideal by construction. Let us prove that it is also a two-sided coideal.
First of all, let us collect some observations that will be needed afterward. Recall from Corollary 2.8 that we have a natural
![]() ${\mathcal H}$
-action on
${\mathcal H}$
-action on
![]() ${\mathcal H} \otimes _{A} {\mathcal H}$
given by
${\mathcal H} \otimes _{A} {\mathcal H}$
given by
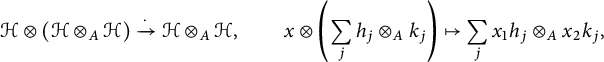 $$ \begin{align} {\mathcal H} \otimes ({\mathcal H} \otimes_{A} {\mathcal H}) \xrightarrow{\cdot} {\mathcal H} \otimes_{A} {\mathcal H}, \qquad x \otimes \left(\sum_j h_j \otimes_{A} k_j\right) \mapsto \sum_{j} x_1h_j \otimes_{A} x_2k_j, \end{align} $$
$$ \begin{align} {\mathcal H} \otimes ({\mathcal H} \otimes_{A} {\mathcal H}) \xrightarrow{\cdot} {\mathcal H} \otimes_{A} {\mathcal H}, \qquad x \otimes \left(\sum_j h_j \otimes_{A} k_j\right) \mapsto \sum_{j} x_1h_j \otimes_{A} x_2k_j, \end{align} $$
and a natural action of
![]() ${\mathcal H}$
on
${\mathcal H}$
on
![]() ${\mathcal H}/{\mathcal H} B^+ \otimes _{A} {\mathcal H}$
given by
${\mathcal H}/{\mathcal H} B^+ \otimes _{A} {\mathcal H}$
given by
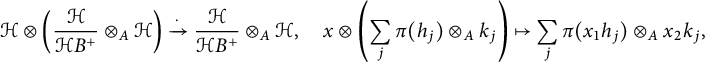 $$ \begin{align} {\mathcal H} \otimes \left(\frac{{\mathcal H}}{{\mathcal H} B^+} \otimes_{A} {\mathcal H}\right) \xrightarrow{\cdot} \frac{{\mathcal H}}{{\mathcal H} B^+} \otimes_{A} {\mathcal H}, \quad x \otimes \left(\sum_j \pi(h_j) \otimes_{A} k_j\right) \mapsto \sum_{j} \pi(x_1h_j) \otimes_{A} x_2k_j, \end{align} $$
$$ \begin{align} {\mathcal H} \otimes \left(\frac{{\mathcal H}}{{\mathcal H} B^+} \otimes_{A} {\mathcal H}\right) \xrightarrow{\cdot} \frac{{\mathcal H}}{{\mathcal H} B^+} \otimes_{A} {\mathcal H}, \quad x \otimes \left(\sum_j \pi(h_j) \otimes_{A} k_j\right) \mapsto \sum_{j} \pi(x_1h_j) \otimes_{A} x_2k_j, \end{align} $$
where
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/{\mathcal H} B^+$
is the canonical projection. Moreover,
$\pi \colon {\mathcal H} \to {\mathcal H}/{\mathcal H} B^+$
is the canonical projection. Moreover,
![]() $B\subseteq {\mathcal H}$
is a right
$B\subseteq {\mathcal H}$
is a right
![]() ${\mathcal H}$
-comodule with a right A-linear coaction
${\mathcal H}$
-comodule with a right A-linear coaction
![]() $\delta \colon {B}{}_{t^{\mathrm {o}}} \to {B}{}_{t^{\mathrm {o}}} \otimes _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
such that (3.3) commutes, that is, for every
$\delta \colon {B}{}_{t^{\mathrm {o}}} \to {B}{}_{t^{\mathrm {o}}} \otimes _{A} {}_{s} {{\mathcal H}}{}_{t^{\mathrm {o}}}$
such that (3.3) commutes, that is, for every
![]() $b \in B$
, we have
$b \in B$
, we have
Therefore, (3.8) induces an action of B on
![]() ${\mathcal H} \otimes _{A} {\mathcal H}$
via restriction of scalars along
${\mathcal H} \otimes _{A} {\mathcal H}$
via restriction of scalars along
![]() $\iota $
,
$\iota $
,
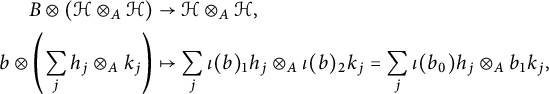 $$ \begin{align*} B \otimes \left({\mathcal H} \otimes_{A} {\mathcal H}\right) & \to {\mathcal H} \otimes_{A} {\mathcal H}, \\ b \otimes \left(\sum_j h_j \otimes_{A} k_j\right) & \mapsto \sum_{j} \iota(b)_1h_j \otimes_{A} \iota(b)_2k_j = \sum_{j} \iota(b_0)h_j \otimes_{A} b_{1}k_j, \end{align*} $$
$$ \begin{align*} B \otimes \left({\mathcal H} \otimes_{A} {\mathcal H}\right) & \to {\mathcal H} \otimes_{A} {\mathcal H}, \\ b \otimes \left(\sum_j h_j \otimes_{A} k_j\right) & \mapsto \sum_{j} \iota(b)_1h_j \otimes_{A} \iota(b)_2k_j = \sum_{j} \iota(b_0)h_j \otimes_{A} b_{1}k_j, \end{align*} $$
with respect to which
![]() $\Delta \colon {\mathcal H} \to {\mathcal H} \otimes _{A} {\mathcal H}$
becomes left B-linear:
$\Delta \colon {\mathcal H} \to {\mathcal H} \otimes _{A} {\mathcal H}$
becomes left B-linear:
Similarly, (3.9) induces an action of B on
![]() ${\mathcal H}/{\mathcal H} B^+ \otimes _{A} {\mathcal H}$
. In particular, (3.8) and (3.9) themselves factor through the tensor product over B (by associativity of the multiplication in
${\mathcal H}/{\mathcal H} B^+ \otimes _{A} {\mathcal H}$
. In particular, (3.8) and (3.9) themselves factor through the tensor product over B (by associativity of the multiplication in
![]() ${\mathcal H}$
):
${\mathcal H}$
):
Furthermore, we have a well-defined action of B on
![]() $B \otimes _{A} {\mathcal H}$
:
$B \otimes _{A} {\mathcal H}$
:
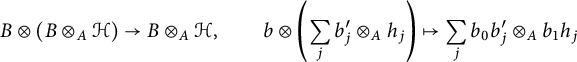 $$ \begin{align*} B \otimes \left(B \otimes_{A} {\mathcal H}\right) \to B \otimes_{A} {\mathcal H}, \qquad b \otimes \left(\sum_j b^{\prime}_j \otimes_{A} h_j\right) \mapsto \sum_{j} b_0b^{\prime}_j \otimes_{A} b_{1}h_j \end{align*} $$
$$ \begin{align*} B \otimes \left(B \otimes_{A} {\mathcal H}\right) \to B \otimes_{A} {\mathcal H}, \qquad b \otimes \left(\sum_j b^{\prime}_j \otimes_{A} h_j\right) \mapsto \sum_{j} b_0b^{\prime}_j \otimes_{A} b_{1}h_j \end{align*} $$
and
![]() $\delta \colon B \to B \otimes _{A} {\mathcal H}$
becomes left B-linear with respect to this B-module structure and the regular B-action on the domain. By summing up all the informations we collected, we have a commutative diagram of left
$\delta \colon B \to B \otimes _{A} {\mathcal H}$
becomes left B-linear with respect to this B-module structure and the regular B-action on the domain. By summing up all the informations we collected, we have a commutative diagram of left
![]() ${\mathcal H}$
-modules and left
${\mathcal H}$
-modules and left
![]() ${\mathcal H}$
-module homomorphisms
${\mathcal H}$
-module homomorphisms
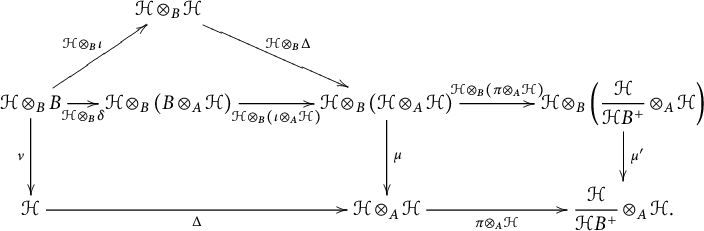
In view of this, for every
![]() $\sum _i h_i \iota (b_i) \in {\mathcal H} B$
, we have
$\sum _i h_i \iota (b_i) \in {\mathcal H} B$
, we have
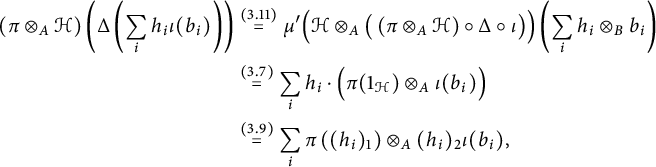 $$ \begin{align*} \begin{aligned} (\pi \otimes_{A} {\mathcal H})\left(\Delta\left(\sum_i h_i \iota(b_i)\right)\right) & \stackrel{(3.11)}{=} \mu' \Big({\mathcal H} \otimes_{A} \big(\left(\pi \otimes_{A} {\mathcal H}\right)\circ \Delta \circ \iota\big)\Big)\left(\sum_i h_i \otimes_{B} b_i\right) \\ & \stackrel{(3.7)}{=} \sum_i h_i \cdot \Big(\pi(1_{\mathcal H})\otimes_{A} \iota(b_i)\Big) \\ & \stackrel{(3.9)}{=} \sum_i \pi\left((h_i)_1\right) \otimes_{A} (h_i)_2\iota(b_i), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (\pi \otimes_{A} {\mathcal H})\left(\Delta\left(\sum_i h_i \iota(b_i)\right)\right) & \stackrel{(3.11)}{=} \mu' \Big({\mathcal H} \otimes_{A} \big(\left(\pi \otimes_{A} {\mathcal H}\right)\circ \Delta \circ \iota\big)\Big)\left(\sum_i h_i \otimes_{B} b_i\right) \\ & \stackrel{(3.7)}{=} \sum_i h_i \cdot \Big(\pi(1_{\mathcal H})\otimes_{A} \iota(b_i)\Big) \\ & \stackrel{(3.9)}{=} \sum_i \pi\left((h_i)_1\right) \otimes_{A} (h_i)_2\iota(b_i), \end{aligned} \end{align*} $$
and hence for all
![]() $\sum _i h_i \iota (b_i) \in {\mathcal H} B^+$
, we have
$\sum _i h_i \iota (b_i) \in {\mathcal H} B^+$
, we have
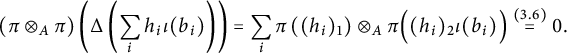 $$ \begin{align*} (\pi \otimes_{A} \pi)\left(\Delta\left(\sum_i h_i \iota(b_i) \right)\right) = \sum_i \pi\left((h_i)_1\right) \otimes_{A} \pi\Big((h_i)_2 \iota(b_i)\Big) \stackrel{(3.6)}{=} 0. \end{align*} $$
$$ \begin{align*} (\pi \otimes_{A} \pi)\left(\Delta\left(\sum_i h_i \iota(b_i) \right)\right) = \sum_i \pi\left((h_i)_1\right) \otimes_{A} \pi\Big((h_i)_2 \iota(b_i)\Big) \stackrel{(3.6)}{=} 0. \end{align*} $$
Since, in addition,
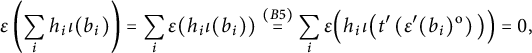 $$ \begin{align*} \varepsilon\left(\sum_i h_i \iota(b_i)\right) = \sum_i \varepsilon(h_i \iota(b_i)) \stackrel{(B5)}{=} \sum_i \varepsilon\Big(h_i \iota \big(t'\left(\varepsilon'(b_i)^{\mathrm{o}}\right)\big)\Big) = 0, \end{align*} $$
$$ \begin{align*} \varepsilon\left(\sum_i h_i \iota(b_i)\right) = \sum_i \varepsilon(h_i \iota(b_i)) \stackrel{(B5)}{=} \sum_i \varepsilon\Big(h_i \iota \big(t'\left(\varepsilon'(b_i)^{\mathrm{o}}\right)\big)\Big) = 0, \end{align*} $$
we have that
![]() ${\mathcal H} B^+$
is a two-sided coideal (in view of [Reference Brzeziński and Wisbauer7, Paragraph 17.14], for instance). Again, it is evident that if
${\mathcal H} B^+$
is a two-sided coideal (in view of [Reference Brzeziński and Wisbauer7, Paragraph 17.14], for instance). Again, it is evident that if
![]() $B \subseteq \tilde {B}$
, then
$B \subseteq \tilde {B}$
, then
![]() ${\mathcal H} B^+ \subseteq {\mathcal H} \tilde {B}^+$
. Thus, the correspondence is inclusion-preserving.
${\mathcal H} B^+ \subseteq {\mathcal H} \tilde {B}^+$
. Thus, the correspondence is inclusion-preserving.
3.1.5 The canonical inclusions
Proposition 3.7 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid over A. Let B be a right
$(A,{\mathcal H})$
be a left bialgebroid over A. Let B be a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring via t of
$A^{\mathrm {o}}$
-subring via t of
![]() ${\mathcal H}$
. In view of Proposition 3.6, we know that
${\mathcal H}$
. In view of Proposition 3.6, we know that
![]() ${\mathcal H} B^+$
is a left ideal two-sided coideal in
${\mathcal H} B^+$
is a left ideal two-sided coideal in
![]() ${\mathcal H}$
. Denote by
${\mathcal H}$
. Denote by
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/{\mathcal H} B^+$
the canonical projection. Then the inclusion
$\pi \colon {\mathcal H} \to {\mathcal H}/{\mathcal H} B^+$
the canonical projection. Then the inclusion
![]() $\iota \colon B \to {\mathcal H}$
factors through
$\iota \colon B \to {\mathcal H}$
factors through
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
. That is to say, we have an inclusion
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
. That is to say, we have an inclusion
![]() ${B \subseteq {{\mathcal H}}^{\textsf { co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}}$
, which we denote by
${B \subseteq {{\mathcal H}}^{\textsf { co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}}$
, which we denote by
![]() $\eta _B$
, such that
$\eta _B$
, such that
![]() $\iota = j'\circ \eta _B$
where
$\iota = j'\circ \eta _B$
where
![]() $j'\colon {{\mathcal H}}^{\textsf { co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}} \to {\mathcal H}$
is the canonical inclusion.
$j'\colon {{\mathcal H}}^{\textsf { co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}} \to {\mathcal H}$
is the canonical inclusion.
Proof Recall that
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
can be realized as the following equalizer in
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
can be realized as the following equalizer in
![]() $\textsf {Mod}_{A}$
:
$\textsf {Mod}_{A}$
:

(see (3.5)). By (3.7), there exists
![]() $\eta _B\colon B \to {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
such that
$\eta _B\colon B \to {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
such that
![]() $\iota \colon B \to {\mathcal H}$
factors as
$\iota \colon B \to {\mathcal H}$
factors as
![]() ${j'\circ \eta _B}$
.
${j'\circ \eta _B}$
.
Proposition 3.8 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid over A such that
$(A,{\mathcal H})$
be a left bialgebroid over A such that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let I be a left ideal two-sided coideal in
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let I be a left ideal two-sided coideal in
![]() ${\mathcal H}$
. In view of Proposition 3.4, we know that
${\mathcal H}$
. In view of Proposition 3.4, we know that
![]() is a right
is a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t. Then we have an inclusion
${\mathcal H}$
via t. Then we have an inclusion
![]() ${\mathcal H} B^+ \subseteq I$
that we denote by
${\mathcal H} B^+ \subseteq I$
that we denote by
![]() $\epsilon _I$
.
$\epsilon _I$
.
Proof Notice that
![]() $\overline {{\mathcal H}} = {\mathcal H}/I$
is clearly an object in
$\overline {{\mathcal H}} = {\mathcal H}/I$
is clearly an object in
. Set
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
. If we consider
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
. If we consider
![]() ${\overline {{\mathcal H}}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, then it is not hard to show that the correspondence defined by
${\overline {{\mathcal H}}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, then it is not hard to show that the correspondence defined by
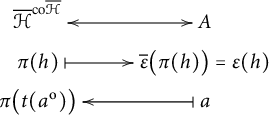
is a left B-linear isomorphism, where the B-module structures are both induced by the
![]() ${\mathcal H}$
-module structures via restriction of scalars along
${\mathcal H}$
-module structures via restriction of scalars along
![]() $\iota \colon B \to {\mathcal H}$
. In fact, for every
$\iota \colon B \to {\mathcal H}$
. In fact, for every
![]() $\pi (h) \in {\overline {{\mathcal H}}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, we have
$\pi (h) \in {\overline {{\mathcal H}}}^{\textsf {co}{\overline {{\mathcal H}}}}$
, we have
and so
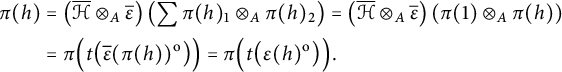 $$ \begin{align*} \pi(h) & = \left(\overline{{\mathcal H}} \otimes_{A} \overline{\varepsilon}\right)\left(\sum \pi(h)_1 \otimes_{A} \pi(h)_2\right) = \left(\overline{{\mathcal H}} \otimes_{A} \overline{\varepsilon}\right)\left(\pi(1) \otimes_{A} \pi(h)\right) \\ & = \pi\Big(t\big(\overline{\varepsilon}(\pi(h))^{\mathrm{o}}\big)\Big) = \pi\Big(t\big(\varepsilon(h)^{\mathrm{o}}\big)\Big). \end{align*} $$
$$ \begin{align*} \pi(h) & = \left(\overline{{\mathcal H}} \otimes_{A} \overline{\varepsilon}\right)\left(\sum \pi(h)_1 \otimes_{A} \pi(h)_2\right) = \left(\overline{{\mathcal H}} \otimes_{A} \overline{\varepsilon}\right)\left(\pi(1) \otimes_{A} \pi(h)\right) \\ & = \pi\Big(t\big(\overline{\varepsilon}(\pi(h))^{\mathrm{o}}\big)\Big) = \pi\Big(t\big(\varepsilon(h)^{\mathrm{o}}\big)\Big). \end{align*} $$
This proves that the correspondence is bijective. To prove that it is left B-linear, notice that
Since, in addition, we know from a short exact sequence like (3.1) that
![]() $A \cong B/B^+$
as left B-module, we may consider the composition
$A \cong B/B^+$
as left B-module, we may consider the composition
explicitly given by
![]() $h + {\mathcal H} B^+ \mapsto \pi (h) = h + I$
for all
$h + {\mathcal H} B^+ \mapsto \pi (h) = h + I$
for all
![]() $h \in {\mathcal H}$
, where
$h \in {\mathcal H}$
, where
![]() $\theta _{\overline {{\mathcal H}}}$
is the
$\theta _{\overline {{\mathcal H}}}$
is the
![]() $\overline {{\mathcal H}}$
-component of the counit (2.15). Denote it by
$\overline {{\mathcal H}}$
-component of the counit (2.15). Denote it by
![]() $\psi $
and consider the commutative diagram
$\psi $
and consider the commutative diagram
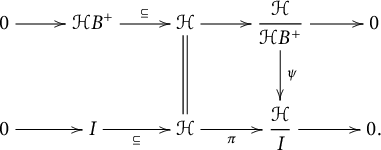
It follows that
![]() ${\mathcal H} B^+ \subseteq I$
as claimed.
${\mathcal H} B^+ \subseteq I$
as claimed.
Theorem 3.9 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid such that
$(A,{\mathcal H})$
be a left bialgebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat.
${}_{s} {{{\mathcal H}}}$
is A-flat.
-
(1) If I is a left ideal two-sided coideal in
 ${\mathcal H}$
and if
${\mathcal H}$
and if
 , then
, then
 $B = {{\mathcal H}}^{\textsf { co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
. That is,
$B = {{\mathcal H}}^{\textsf { co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
. That is,
 $\Psi \Phi \Psi (I) = \Psi (I)$
.
$\Psi \Phi \Psi (I) = \Psi (I)$
. -
(2) If B is a right
 ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
 $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
 ${\mathcal H}$
via t and if
${\mathcal H}$
via t and if
 , then
, then
 ${I = {\mathcal H} \left ({{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\right )^+}$
. That is,
${I = {\mathcal H} \left ({{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\right )^+}$
. That is,
 $\Phi \Psi \Phi (B) = \Phi (B)$
.
$\Phi \Psi \Phi (B) = \Phi (B)$
.
In other words,
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
form a monotone Galois connection (or, equivalently, an adjunction) between the two lattices.
$\Psi $
form a monotone Galois connection (or, equivalently, an adjunction) between the two lattices.
Proof Flatness is needed to apply Proposition 3.4. Recall that for any left ideal two-sided coideal I and for any right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t, we have that
${\mathcal H}$
via t, we have that
![]() ${B \subseteq {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}}$
via
${B \subseteq {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}}$
via
![]() $\eta _B$
and
$\eta _B$
and
![]() ${\mathcal H} \left ({{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\right )^+ \subseteq I$
via
${\mathcal H} \left ({{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\right )^+ \subseteq I$
via
![]() $\epsilon _I$
, by Propositions 3.7 and 3.8, respectively.
$\epsilon _I$
, by Propositions 3.7 and 3.8, respectively.
-
(1) Let I be a left ideal two-sided coideal in
 ${\mathcal H}$
, and let
${\mathcal H}$
, and let
 . Since
. Since
 ${\mathcal H} B^+ \subseteq I$
, we have a surjective morphism of left
${\mathcal H} B^+ \subseteq I$
, we have a surjective morphism of left
 ${\mathcal H}$
-module corings
${\mathcal H}$
-module corings
 ${\mathcal H}/{\mathcal H} B^+ \twoheadrightarrow {\mathcal H}/I$
such that
${\mathcal H}/{\mathcal H} B^+ \twoheadrightarrow {\mathcal H}/I$
such that 
commutes and hence
 $$ \begin{align*}B \subseteq {{\mathcal H}}^{\textsf{co}{\frac{{\mathcal H}}{{\mathcal H} B^+}}} \subseteq {{\mathcal H}}^{\textsf{co}{\frac{{\mathcal H}}{I}}} = B.\end{align*} $$
$$ \begin{align*}B \subseteq {{\mathcal H}}^{\textsf{co}{\frac{{\mathcal H}}{{\mathcal H} B^+}}} \subseteq {{\mathcal H}}^{\textsf{co}{\frac{{\mathcal H}}{I}}} = B.\end{align*} $$
-
(2) Let B be a right
 ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
 $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
 ${\mathcal H}$
via t and set
${\mathcal H}$
via t and set
 . Since
. Since
 $B \subseteq {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}} = {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, we have that
$B \subseteq {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}} = {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, we have that  $$ \begin{align*}I = {\mathcal H} B^+ \subseteq {\mathcal H} \left({{\mathcal H}}^{\textsf{co}{\frac{{\mathcal H}}{I}}}\right)^+ \subseteq I.\\[-37pt] \end{align*} $$
$$ \begin{align*}I = {\mathcal H} B^+ \subseteq {\mathcal H} \left({{\mathcal H}}^{\textsf{co}{\frac{{\mathcal H}}{I}}}\right)^+ \subseteq I.\\[-37pt] \end{align*} $$
Corollary 3.10 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid such that
$(A,{\mathcal H})$
be a left bialgebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat. For I a left ideal two-sided coideal in
${}_{s} {{{\mathcal H}}}$
is A-flat. For I a left ideal two-sided coideal in
![]() ${\mathcal H}$
and B a right
${\mathcal H}$
and B a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring via t of
$A^{\mathrm {o}}$
-subring via t of
![]() ${\mathcal H}$
, we have that
${\mathcal H}$
, we have that
Proof This is simply a restatement of the fact that
![]() $\Phi $
is left adjoint to
$\Phi $
is left adjoint to
![]() $\Psi $
.
$\Psi $
.
3.2 The Hopf algebroid case and the bijective correspondence
In case the bialgebroid
![]() $(A,{\mathcal H})$
is a left Hopf algebroid, one can obtain finer results on the correspondence between left ideal two-sided coideals and right comodule subrings than those in Propositions 3.4 and 3.6, as we are going to show in the present subsection.
$(A,{\mathcal H})$
is a left Hopf algebroid, one can obtain finer results on the correspondence between left ideal two-sided coideals and right comodule subrings than those in Propositions 3.4 and 3.6, as we are going to show in the present subsection.
Remark 3.11 Let
![]() $(A,{\mathcal H})$
be a left bialgebroid over A. We may consider the tensor product
$(A,{\mathcal H})$
be a left bialgebroid over A. We may consider the tensor product
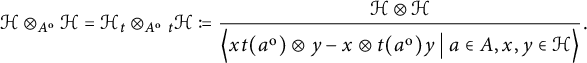
It becomes an
![]() $A^{\mathrm {o}}$
-bimodule via
$A^{\mathrm {o}}$
-bimodule via
for all
![]() $x,y \in {\mathcal H}$
,
$x,y \in {\mathcal H}$
,
![]() $a \in A$
. Inside
$a \in A$
. Inside
![]() ${\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H}$
, we isolate the distinguished subspace
${\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H}$
, we isolate the distinguished subspace
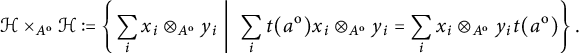
It is an
![]() $A^{\mathrm {o}}$
-subbimodule and a
$A^{\mathrm {o}}$
-subbimodule and a
![]() $\Bbbk $
-algebra with unit
$\Bbbk $
-algebra with unit
![]() $1 \otimes _{A^{\mathrm {o}}} 1^{\mathrm {o}}$
and multiplication
$1 \otimes _{A^{\mathrm {o}}} 1^{\mathrm {o}}$
and multiplication
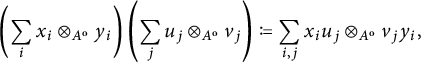
which acts from the right on
![]() ${\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H}$
via
${\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H}$
via
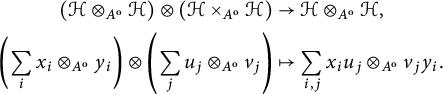 $$ \begin{align} \begin{aligned} \left({\mathcal H} \otimes_{A^{\mathrm{o}}} {\mathcal H}\right)\otimes\left({\mathcal H} \times_{A^{\mathrm{o}}} {\mathcal H}\right) & \to {\mathcal H} \otimes_{A^{\mathrm{o}}} {\mathcal H}, \\ \left(\sum_i x_i \otimes_{A^{\mathrm{o}}} y_i\right)\otimes\left(\sum_j u_j \otimes_{A^{\mathrm{o}}} v_j\right) & \mapsto \sum_{i,j} x_iu_j \otimes_{A^{\mathrm{o}}} v_jy_i. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \left({\mathcal H} \otimes_{A^{\mathrm{o}}} {\mathcal H}\right)\otimes\left({\mathcal H} \times_{A^{\mathrm{o}}} {\mathcal H}\right) & \to {\mathcal H} \otimes_{A^{\mathrm{o}}} {\mathcal H}, \\ \left(\sum_i x_i \otimes_{A^{\mathrm{o}}} y_i\right)\otimes\left(\sum_j u_j \otimes_{A^{\mathrm{o}}} v_j\right) & \mapsto \sum_{i,j} x_iu_j \otimes_{A^{\mathrm{o}}} v_jy_i. \end{aligned} \end{align} $$
If
![]() ${\mathcal H}$
is, in addition, a left Hopf algebroid in the sense of [Reference Schauenburg34, Theorem and Definition 3.5] with canonical map
${\mathcal H}$
is, in addition, a left Hopf algebroid in the sense of [Reference Schauenburg34, Theorem and Definition 3.5] with canonical map
then the assignment
induces a morphism of
![]() $\Bbbk $
-algebras
$\Bbbk $
-algebras
The fact that
![]() $\gamma $
lands into
$\gamma $
lands into
![]() ${\mathcal H} \times _{A^{\mathrm {o}}} {\mathcal H}$
is [Reference Schauenburg34, equation (3.3)], and the fact that it is multiplicative and unital is [Reference Schauenburg34, equations (3.4) and (3.5)]. The map
${\mathcal H} \times _{A^{\mathrm {o}}} {\mathcal H}$
is [Reference Schauenburg34, equation (3.3)], and the fact that it is multiplicative and unital is [Reference Schauenburg34, equations (3.4) and (3.5)]. The map
![]() $\gamma $
is referred to as the the (left) translation map. In particular,
$\gamma $
is referred to as the the (left) translation map. In particular,
for all
![]() $x,y \in {\mathcal H}$
.▲
$x,y \in {\mathcal H}$
.▲
Lemma 3.12 Let
![]() $(A,{\mathcal H})$
be a left Hopf algebroid over A such that
$(A,{\mathcal H})$
be a left Hopf algebroid over A such that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let B be a right
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let B be a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring of
$A^{\mathrm {o}}$
-subring of
![]() ${\mathcal H}$
via t such that for all
${\mathcal H}$
via t such that for all
![]() $b \in B$
, there exists
$b \in B$
, there exists
![]() $\sum _i b_i \otimes _{A^{\mathrm {o}}} h_i \in B \otimes _{A^{\mathrm {o}}} {\mathcal H}$
such that
$\sum _i b_i \otimes _{A^{\mathrm {o}}} h_i \in B \otimes _{A^{\mathrm {o}}} {\mathcal H}$
such that
Then the canonical isomorphism
induces an isomorphism
Proof Consider the composition
It satisfies
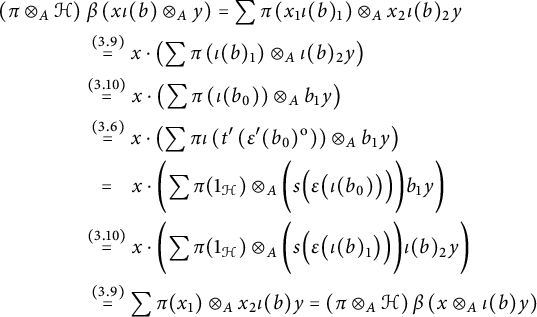 $$ \begin{align*} \left(\pi \otimes_{A}{\mathcal H}\right) & ~ \beta\left(x\iota(b) \otimes_{A} y \right) = \sum \pi\left(x_1\iota(b)_1\right) \otimes_{A} x_2\iota(b)_2y \\ & \hspace{2pt}\stackrel{(3.9)}{=} x \cdot \left(\sum \pi\left(\iota(b)_1\right) \otimes_{A} \iota(b)_2y\right) \\ & \stackrel{(3.10)}{=} x \cdot \left(\sum \pi\left(\iota(b_0)\right) \otimes_{A} b_1y\right) \\ & \hspace{2pt}\stackrel{(3.6)}{=} x \cdot \left(\sum \pi\iota\left(t'\left(\varepsilon'(b_0)^{\mathrm{o}}\right)\right) \otimes_{A} b_1y\right) \\ & \stackrel{\phantom{(3.10)}}{=} x \cdot \left(\sum \pi(1_{{\mathcal H}}) \otimes_{A} \bigg(s\Big(\varepsilon\big(\iota(b_0)\big)\Big)\bigg)b_1y\right) \\ & \stackrel{(3.10)}{=} x \cdot \left(\sum \pi(1_{{\mathcal H}}) \otimes_{A} \bigg(s\Big(\varepsilon\big(\iota(b)_1\big)\Big)\bigg)\iota(b)_2y\right) \\ & \hspace{2pt}\stackrel{(3.9)}{=} \sum \pi(x_1) \otimes_{A} x_2\iota(b)y = \left(\pi \otimes_{A}{\mathcal H}\right)\beta\left(x \otimes_{A} \iota(b)y \right) \end{align*} $$
$$ \begin{align*} \left(\pi \otimes_{A}{\mathcal H}\right) & ~ \beta\left(x\iota(b) \otimes_{A} y \right) = \sum \pi\left(x_1\iota(b)_1\right) \otimes_{A} x_2\iota(b)_2y \\ & \hspace{2pt}\stackrel{(3.9)}{=} x \cdot \left(\sum \pi\left(\iota(b)_1\right) \otimes_{A} \iota(b)_2y\right) \\ & \stackrel{(3.10)}{=} x \cdot \left(\sum \pi\left(\iota(b_0)\right) \otimes_{A} b_1y\right) \\ & \hspace{2pt}\stackrel{(3.6)}{=} x \cdot \left(\sum \pi\iota\left(t'\left(\varepsilon'(b_0)^{\mathrm{o}}\right)\right) \otimes_{A} b_1y\right) \\ & \stackrel{\phantom{(3.10)}}{=} x \cdot \left(\sum \pi(1_{{\mathcal H}}) \otimes_{A} \bigg(s\Big(\varepsilon\big(\iota(b_0)\big)\Big)\bigg)b_1y\right) \\ & \stackrel{(3.10)}{=} x \cdot \left(\sum \pi(1_{{\mathcal H}}) \otimes_{A} \bigg(s\Big(\varepsilon\big(\iota(b)_1\big)\Big)\bigg)\iota(b)_2y\right) \\ & \hspace{2pt}\stackrel{(3.9)}{=} \sum \pi(x_1) \otimes_{A} x_2\iota(b)y = \left(\pi \otimes_{A}{\mathcal H}\right)\beta\left(x \otimes_{A} \iota(b)y \right) \end{align*} $$
for all
![]() $x,y \in {\mathcal H}$
,
$x,y \in {\mathcal H}$
,
![]() $b \in B$
; thus, it factors through
$b \in B$
; thus, it factors through
In the other direction, consider the composition
where p is the canonical projection. Since
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat,
${}_{s} {{{\mathcal H}}}$
is A-flat,
![]() ${\mathcal H} B^+ \otimes _{A} {\mathcal H} \subseteq {\mathcal H} \otimes _{A} {\mathcal H}$
, and, in fact,
${\mathcal H} B^+ \otimes _{A} {\mathcal H} \subseteq {\mathcal H} \otimes _{A} {\mathcal H}$
, and, in fact,
![]() ${\mathcal H} B^+ \otimes _{A} {\mathcal H} = \ker \left (\pi \otimes _{A} {\mathcal H}\right )$
. For all
${\mathcal H} B^+ \otimes _{A} {\mathcal H} = \ker \left (\pi \otimes _{A} {\mathcal H}\right )$
. For all
![]() $\sum _j x_j\iota (b_j) \otimes _{A} y_j \in {\mathcal H} B^+ \otimes _{A} {\mathcal H}$
, we have
$\sum _j x_j\iota (b_j) \otimes _{A} y_j \in {\mathcal H} B^+ \otimes _{A} {\mathcal H}$
, we have
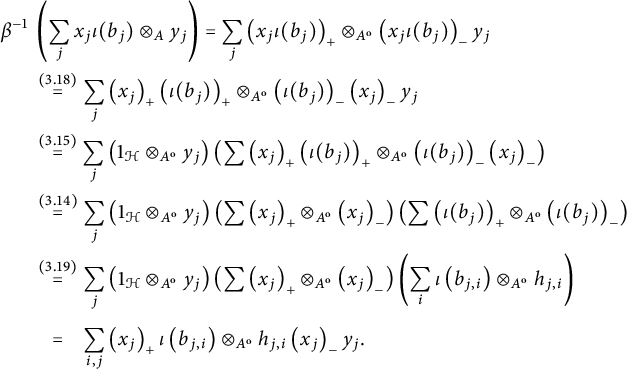 $$ \begin{align*} \beta^{-1} ~ & \left(\sum_j x_j\iota(b_j) \otimes_{A} y_j\right) = \sum_j \left(x_j\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(x_j\iota(b_j)\right)_{-}y_j \\ & \stackrel{(3.18)}{=} \sum_j \left(x_j\right)_{+}\left(\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(\iota(b_j)\right)_{-}\left(x_j\right)_{-}y_j \\ & \stackrel{(3.15)}{=} \sum_j\left(1_{\mathcal H} \otimes_{A^{\mathrm{o}}} y_j\right)\left(\sum\left(x_j\right)_{+}\left(\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(\iota(b_j)\right)_{-}\left(x_j\right)_{-}\right) \\ & \stackrel{(3.14)}{=} \sum_j\left(1_{\mathcal H} \otimes_{A^{\mathrm{o}}} y_j\right)\left(\sum\left(x_j\right)_{+} \otimes_{A^{\mathrm{o}}} \left(x_j\right)_{-}\right)\left(\sum\left(\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(\iota(b_j)\right)_{-}\right) \\ & \stackrel{(3.19)}{=} \sum_j\left(1_{\mathcal H} \otimes_{A^{\mathrm{o}}} y_j\right)\left(\sum\left(x_j\right)_{+} \otimes_{A^{\mathrm{o}}} \left(x_j\right)_{-}\right)\left(\sum_i \iota\left(b_{j,i}\right) \otimes_{A^{\mathrm{o}}} h_{j,i}\right) \\ & \stackrel{\phantom{(3.19)}}{=} \sum_{i,j} \left(x_j\right)_{+}\iota\left(b_{j,i}\right) \otimes_{A^{\mathrm{o}}} h_{j,i}\left(x_j\right)_{-}y_j. \end{align*} $$
$$ \begin{align*} \beta^{-1} ~ & \left(\sum_j x_j\iota(b_j) \otimes_{A} y_j\right) = \sum_j \left(x_j\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(x_j\iota(b_j)\right)_{-}y_j \\ & \stackrel{(3.18)}{=} \sum_j \left(x_j\right)_{+}\left(\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(\iota(b_j)\right)_{-}\left(x_j\right)_{-}y_j \\ & \stackrel{(3.15)}{=} \sum_j\left(1_{\mathcal H} \otimes_{A^{\mathrm{o}}} y_j\right)\left(\sum\left(x_j\right)_{+}\left(\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(\iota(b_j)\right)_{-}\left(x_j\right)_{-}\right) \\ & \stackrel{(3.14)}{=} \sum_j\left(1_{\mathcal H} \otimes_{A^{\mathrm{o}}} y_j\right)\left(\sum\left(x_j\right)_{+} \otimes_{A^{\mathrm{o}}} \left(x_j\right)_{-}\right)\left(\sum\left(\iota(b_j)\right)_{+} \otimes_{A^{\mathrm{o}}} \left(\iota(b_j)\right)_{-}\right) \\ & \stackrel{(3.19)}{=} \sum_j\left(1_{\mathcal H} \otimes_{A^{\mathrm{o}}} y_j\right)\left(\sum\left(x_j\right)_{+} \otimes_{A^{\mathrm{o}}} \left(x_j\right)_{-}\right)\left(\sum_i \iota\left(b_{j,i}\right) \otimes_{A^{\mathrm{o}}} h_{j,i}\right) \\ & \stackrel{\phantom{(3.19)}}{=} \sum_{i,j} \left(x_j\right)_{+}\iota\left(b_{j,i}\right) \otimes_{A^{\mathrm{o}}} h_{j,i}\left(x_j\right)_{-}y_j. \end{align*} $$
Therefore,
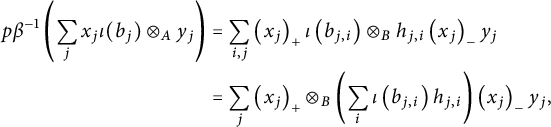 $$ \begin{align*} p\beta^{-1}\left(\sum_j x_j\iota(b_j) \otimes_{A} y_j\right) & = \sum_{i,j} \left(x_j\right)_{+}\iota\left(b_{j,i}\right) \otimes_{B} h_{j,i}\left(x_j\right)_{-}y_j \\ & = \sum_{j} \left(x_j\right)_{+} \otimes_{B} \left(\sum_i\iota\left(b_{j,i}\right)h_{j,i}\right)\left(x_j\right)_{-}y_j, \end{align*} $$
$$ \begin{align*} p\beta^{-1}\left(\sum_j x_j\iota(b_j) \otimes_{A} y_j\right) & = \sum_{i,j} \left(x_j\right)_{+}\iota\left(b_{j,i}\right) \otimes_{B} h_{j,i}\left(x_j\right)_{-}y_j \\ & = \sum_{j} \left(x_j\right)_{+} \otimes_{B} \left(\sum_i\iota\left(b_{j,i}\right)h_{j,i}\right)\left(x_j\right)_{-}y_j, \end{align*} $$
and since
for all j, we conclude that (3.20) induces
which is inverse to
![]() $\xi $
.
$\xi $
.
In view of Lemma 3.12, one obtains the following improvement to Proposition 3.7.
Theorem 3.13 Let
![]() $(A,{\mathcal H})$
be a left Hopf algebroid over A such that
$(A,{\mathcal H})$
be a left Hopf algebroid over A such that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let B be a right
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let B be a right
![]() ${\mathcal H}$
-comodule
${\mathcal H}$
-comodule
![]() $A^{\mathrm {o}}$
-subring via t of
$A^{\mathrm {o}}$
-subring via t of
![]() ${\mathcal H}$
such that
${\mathcal H}$
such that
![]() ${\mathcal H}$
is pure over B on the right and such that
${\mathcal H}$
is pure over B on the right and such that
![]() $\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
. Then
$\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
. Then
![]() $B = {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
, that is,
$B = {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
, that is,
![]() $\Psi \Phi (B) = B$
.
$\Psi \Phi (B) = B$
.
Proof On the one hand, purity of
![]() ${\mathcal H}$
on B entails that
${\mathcal H}$
on B entails that
is an equalizer diagram in
![]() $\textsf {Vect}_{\Bbbk }$
(see Corollary 2.2) and, on the other hand, it entails that
$\textsf {Vect}_{\Bbbk }$
(see Corollary 2.2) and, on the other hand, it entails that
![]() $\iota \otimes _{A^{\mathrm {o}}} {\mathcal H}$
is an injective morphism (see Corollary 2.4), so that the condition
$\iota \otimes _{A^{\mathrm {o}}} {\mathcal H}$
is an injective morphism (see Corollary 2.4), so that the condition
![]() $\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
makes sense. By definition,
$\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
makes sense. By definition,
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
can be realized as the following equalizer in
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
can be realized as the following equalizer in
![]() $\textsf {Vect}_{\Bbbk }$
:
$\textsf {Vect}_{\Bbbk }$
:
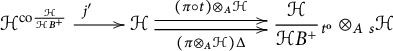
(see (3.5)). Now, commutativity of the following diagram
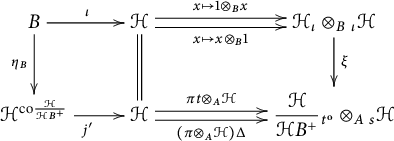
together with bijectivity of
![]() $\xi $
(Lemma 3.12) entails that
$\xi $
(Lemma 3.12) entails that
![]() $\eta _B$
is bijective and hence
$\eta _B$
is bijective and hence
![]() $B = {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
.
$B = {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H} B^+}}}$
.
At the same time, one may obtain the following improvement to Proposition 3.8 by taking advantage of Theorem 2.11.
Theorem 3.14 Let
![]() $(A,{\mathcal H})$
be a left Hopf algebroid over A such that
$(A,{\mathcal H})$
be a left Hopf algebroid over A such that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. Let
![]() $I\subseteq {\mathcal H}$
be a left ideal two-sided coideal such that the extension-of-scalars functor
$I\subseteq {\mathcal H}$
be a left ideal two-sided coideal such that the extension-of-scalars functor
![]() ${\mathcal H} \otimes _{B}-$
is comonadic, where
${\mathcal H} \otimes _{B}-$
is comonadic, where
![]() . Then
. Then
![]() $I = {\mathcal H} B^+$
, that is to say,
$I = {\mathcal H} B^+$
, that is to say,
![]() $\Phi \Psi (I)=I$
.
$\Phi \Psi (I)=I$
.
Proof First of all, observe that the comonadicity of
![]() ${\mathcal H} \otimes _{B}-$
entails that
${\mathcal H} \otimes _{B}-$
entails that
![]() $\iota \colon B \to {\mathcal H}$
is pure as a morphism of right
$\iota \colon B \to {\mathcal H}$
is pure as a morphism of right
![]() $A^{\mathrm {o}}$
-modules, in view of [Reference Janelidze and Tholen23, Section 5.3, Theorem] and Corollary 2.4. Thus, let us start by proving that
$A^{\mathrm {o}}$
-modules, in view of [Reference Janelidze and Tholen23, Section 5.3, Theorem] and Corollary 2.4. Thus, let us start by proving that
![]() $\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
(which now makes sense, because
$\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
(which now makes sense, because
![]() $\iota \otimes _{A^{\mathrm {o}}}{\mathcal H}$
is injective by purity). In a nutshell, the following diagram whose rows are equalizers commutes sequentially:
$\iota \otimes _{A^{\mathrm {o}}}{\mathcal H}$
is injective by purity). In a nutshell, the following diagram whose rows are equalizers commutes sequentially:
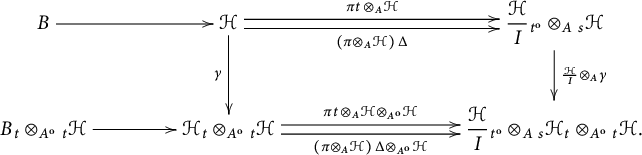
In more detail, we want show that for any
![]() $b\in B$
,
$b\in B$
,
![]() $\gamma (b)= \sum b_{+}\otimes _{A^{\mathrm {o}}} b_{-}\in B \otimes _{A^{\mathrm {o}}} {\mathcal H}$
. Since
$\gamma (b)= \sum b_{+}\otimes _{A^{\mathrm {o}}} b_{-}\in B \otimes _{A^{\mathrm {o}}} {\mathcal H}$
. Since
![]() $\iota \colon B \to {\mathcal H}$
is pure, it follows that
$\iota \colon B \to {\mathcal H}$
is pure, it follows that
![]() $ B \otimes _{A^{\mathrm {o}}}{\mathcal H} = {({\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H})}^{\textsf { co}{\frac {{\mathcal H}}{I}}}$
where
$ B \otimes _{A^{\mathrm {o}}}{\mathcal H} = {({\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H})}^{\textsf { co}{\frac {{\mathcal H}}{I}}}$
where
![]() ${\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H}$
is considered as a left
${\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H}$
is considered as a left
![]() ${\mathcal H}/I$
-comodule via
${\mathcal H}/I$
-comodule via
![]() $(\pi \otimes _{A}\operatorname {Id}_{{\mathcal H}})\Delta \otimes _{A^{\mathrm {o}}}\operatorname {Id}_{{\mathcal H}}$
. On the other hand, we have that
$(\pi \otimes _{A}\operatorname {Id}_{{\mathcal H}})\Delta \otimes _{A^{\mathrm {o}}}\operatorname {Id}_{{\mathcal H}}$
. On the other hand, we have that
![]() $\sum b_{1}\otimes _{A} b_{2} \in 1 \otimes _{A} B + {}_{t} {I} \otimes _{A} {\mathcal H}$
. By equation (3.6) of [Reference Schauenburg34], we have that
$\sum b_{1}\otimes _{A} b_{2} \in 1 \otimes _{A} B + {}_{t} {I} \otimes _{A} {\mathcal H}$
. By equation (3.6) of [Reference Schauenburg34], we have that
Hence,
![]() $\gamma (b)\in {({\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H})}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
.
$\gamma (b)\in {({\mathcal H} \otimes _{A^{\mathrm {o}}} {\mathcal H})}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
.
Now, the additional condition on
![]() $\gamma (B)$
we proved above ensures that
$\gamma (B)$
we proved above ensures that
![]() $\xi $
of (2.14) is an isomorphism in view of Lemma 3.12. In particular,
$\xi $
of (2.14) is an isomorphism in view of Lemma 3.12. In particular,
![]() ${\mathcal K}$
of Theorem 2.11 is an equivalence of categories. Therefore, the morphism
${\mathcal K}$
of Theorem 2.11 is an equivalence of categories. Therefore, the morphism
![]() $\theta _{\overline {{\mathcal H}}}$
in (3.12) from the proof of Proposition 3.8 is an isomorphism, and hence the vertical arrows in (3.13) are all isomorphisms. It follows that
$\theta _{\overline {{\mathcal H}}}$
in (3.12) from the proof of Proposition 3.8 is an isomorphism, and hence the vertical arrows in (3.13) are all isomorphisms. It follows that
![]() $I = {\mathcal H} B^+$
as claimed.
$I = {\mathcal H} B^+$
as claimed.
Summing up, we have the first main result of this work. The functor
![]() ${\mathcal H} \otimes _{B} -$
in the statement below denotes the extension of scalars functor
${\mathcal H} \otimes _{B} -$
in the statement below denotes the extension of scalars functor
![]() ${{}_B\textsf{Mod}}\to {{}_{{\mathcal H}}\textsf {Mod}}$
.
${{}_B\textsf{Mod}}\to {{}_{{\mathcal H}}\textsf {Mod}}$
.
Theorem 3.15 Let
![]() $(A,{\mathcal H})$
be a left Hopf algebroid over A such that
$(A,{\mathcal H})$
be a left Hopf algebroid over A such that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. We have a well-defined inclusion-preserving bijective correspondence
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. We have a well-defined inclusion-preserving bijective correspondence

Proof It follows from Theorem 3.13 (in view of [Reference Janelidze and Tholen23, Section 5.3, Theorem]) and Theorem 3.14.
Corollary 3.16 (of Theorem 3.15)
Let
![]() $(A,{\mathcal H})$
be a left Hopf algebroid over A such that
$(A,{\mathcal H})$
be a left Hopf algebroid over A such that
![]() ${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. We have a well-defined inclusion-preserving bijective correspondence
${}_{s} {{{\mathcal H}}} = {}_{{A\otimes _{}1^{\mathrm {o}}}}{\mathcal H}$
is A-flat. We have a well-defined inclusion-preserving bijective correspondence

Proof It follows from Theorem 3.15, once recalled that if
![]() ${\mathcal H}_B$
is faithfully flat, then
${\mathcal H}_B$
is faithfully flat, then
![]() ${\mathcal H} \otimes _{B} -$
is comonadic.
${\mathcal H} \otimes _{B} -$
is comonadic.
Remark 3.17 The technical-looking condition “
![]() $\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
” is automatically satisfied in most of the cases of interest. Apart from the many particular cases we consider below, in general, it holds in case the Hopf algebroid has an antipode
$\gamma (B)\subseteq B \otimes _{A^{\mathrm {o}}}{\mathcal H}$
” is automatically satisfied in most of the cases of interest. Apart from the many particular cases we consider below, in general, it holds in case the Hopf algebroid has an antipode
![]() $S:{\mathcal H}\to {\mathcal H}$
, i.e., if it is a Hopf algebroid in the sense of Böhm (see [Reference Böhm3, Definition 4.1]). Indeed, in this case, we have that the translation map is given explicitly by
$S:{\mathcal H}\to {\mathcal H}$
, i.e., if it is a Hopf algebroid in the sense of Böhm (see [Reference Böhm3, Definition 4.1]). Indeed, in this case, we have that the translation map is given explicitly by
![]() $\gamma (b)=b_{(1)}\otimes S(b_{(2)})$
, so the condition is clearly fulfilled.
$\gamma (b)=b_{(1)}\otimes S(b_{(2)})$
, so the condition is clearly fulfilled.
The purity of
![]() ${\mathcal H}$
over B, for example, in Theorem 3.13, cannot be avoided in general, as the subsequent example shows.
${\mathcal H}$
over B, for example, in Theorem 3.13, cannot be avoided in general, as the subsequent example shows.
Example 3.18 Let A be any commutative algebra,
![]() , and
, and
![]() . Recall that
. Recall that
![]() $A \otimes A$
admits a Hopf algebroid structure as in [Reference Lu25, Example 3.1]:
$A \otimes A$
admits a Hopf algebroid structure as in [Reference Lu25, Example 3.1]:
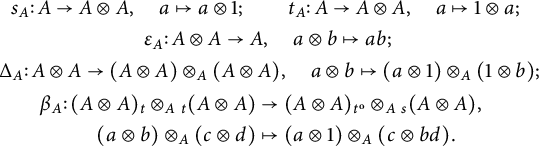 $$ \begin{align*} &\kern6pt s_A\colon A \to A \otimes A, \quad a \mapsto a \otimes 1; \qquad t_A\colon A \to A \otimes A, \quad a \mapsto 1 \otimes a; \\&\kern70pt \varepsilon_A\colon A \otimes A \to A, \quad a \otimes b \mapsto ab; \\&\Delta_A \colon A \otimes A \to (A \otimes A) \otimes_{A} (A \otimes A), \quad a \otimes b \mapsto (a \otimes 1) \otimes_{A} (1\otimes b); \\&\kern20pt\begin{aligned} \beta_A\colon {(A \otimes A)}{}_{t} \otimes_{A} {}_{t} {(A \otimes A)} & \to {(A \otimes A)}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{(A \otimes A)}}, \\ (a \otimes b) \otimes_{A} (c \otimes d) & \mapsto (a \otimes 1) \otimes_{A} (c \otimes bd). \end{aligned} \end{align*} $$
$$ \begin{align*} &\kern6pt s_A\colon A \to A \otimes A, \quad a \mapsto a \otimes 1; \qquad t_A\colon A \to A \otimes A, \quad a \mapsto 1 \otimes a; \\&\kern70pt \varepsilon_A\colon A \otimes A \to A, \quad a \otimes b \mapsto ab; \\&\Delta_A \colon A \otimes A \to (A \otimes A) \otimes_{A} (A \otimes A), \quad a \otimes b \mapsto (a \otimes 1) \otimes_{A} (1\otimes b); \\&\kern20pt\begin{aligned} \beta_A\colon {(A \otimes A)}{}_{t} \otimes_{A} {}_{t} {(A \otimes A)} & \to {(A \otimes A)}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{(A \otimes A)}}, \\ (a \otimes b) \otimes_{A} (c \otimes d) & \mapsto (a \otimes 1) \otimes_{A} (c \otimes bd). \end{aligned} \end{align*} $$
In fact, being a commutative Hopf algebroid,
![]() $A \otimes A$
admits an antipode
$A \otimes A$
admits an antipode
such that
![]() $\beta _A^{-1}(x \otimes _{A} y) = \sum x_1 \otimes _{A} {\mathcal S}_A(x_2)y$
, that is,
$\beta _A^{-1}(x \otimes _{A} y) = \sum x_1 \otimes _{A} {\mathcal S}_A(x_2)y$
, that is,
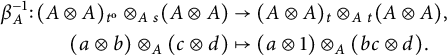 $$ \begin{align*} \beta_A^{-1}\colon {(A \otimes A)}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{(A \otimes A)}} & \to {(A \otimes A)}{}_{t} \otimes_{A} {}_{t} {(A \otimes A)}, \\ (a \otimes b) \otimes_{A} (c \otimes d) & \mapsto (a \otimes 1) \otimes_{A} (bc \otimes d). \end{align*} $$
$$ \begin{align*} \beta_A^{-1}\colon {(A \otimes A)}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{(A \otimes A)}} & \to {(A \otimes A)}{}_{t} \otimes_{A} {}_{t} {(A \otimes A)}, \\ (a \otimes b) \otimes_{A} (c \otimes d) & \mapsto (a \otimes 1) \otimes_{A} (bc \otimes d). \end{align*} $$
We equip B (resp.
![]() ${\mathcal H}$
) with the bialgebroid (resp. Hopf algebroid) structure coming from the base ring extension of the bialgebra
${\mathcal H}$
) with the bialgebroid (resp. Hopf algebroid) structure coming from the base ring extension of the bialgebra
![]() $\Bbbk [X]$
(resp. Hopf algebra
$\Bbbk [X]$
(resp. Hopf algebra
![]() $\Bbbk [X^{\pm 1}]$
) along the morphism
$\Bbbk [X^{\pm 1}]$
) along the morphism
![]() $\Bbbk \to A \otimes A$
(see, for instance, [Reference El Kaoutit12, Example 1.4] and [Reference El Kaoutit13, Example 3.3]). This is a particular instance of the Connes–Moscovici bialgebroid construction, in which all the actions of the bialgebra (resp. Hopf algebra) on the base algebra A are trivial (see [Reference Connes and Moscovici8, Reference Kadison, Brzeziński, Pardo, Shestakov and Smith24] for the original constructions and [Reference Saracco32] for the straightforward adaptation to the bialgebra setting). Namely, we have
$\Bbbk \to A \otimes A$
(see, for instance, [Reference El Kaoutit12, Example 1.4] and [Reference El Kaoutit13, Example 3.3]). This is a particular instance of the Connes–Moscovici bialgebroid construction, in which all the actions of the bialgebra (resp. Hopf algebra) on the base algebra A are trivial (see [Reference Connes and Moscovici8, Reference Kadison, Brzeziński, Pardo, Shestakov and Smith24] for the original constructions and [Reference Saracco32] for the straightforward adaptation to the bialgebra setting). Namely, we have
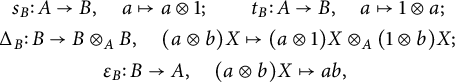 $$ \begin{align*} & \kern6pt s_B\colon A \to B, \quad a \mapsto a \otimes 1; \qquad t_B\colon A \to B, \quad a \mapsto 1 \otimes a; \\&\Delta_B \colon B \to B \otimes_{A} B, \quad (a \otimes b)X \mapsto (a \otimes 1)X \otimes_{A} (1\otimes b)X; \\& \kern50pt \varepsilon_B\colon B \to A, \quad (a \otimes b)X \mapsto ab, \end{align*} $$
$$ \begin{align*} & \kern6pt s_B\colon A \to B, \quad a \mapsto a \otimes 1; \qquad t_B\colon A \to B, \quad a \mapsto 1 \otimes a; \\&\Delta_B \colon B \to B \otimes_{A} B, \quad (a \otimes b)X \mapsto (a \otimes 1)X \otimes_{A} (1\otimes b)X; \\& \kern50pt \varepsilon_B\colon B \to A, \quad (a \otimes b)X \mapsto ab, \end{align*} $$
and
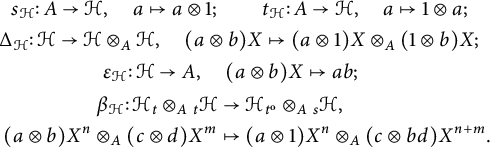 $$ \begin{align*} & \kern6pt s_{\mathcal H}\colon A \to {\mathcal H}, \quad a \mapsto a \otimes 1; \qquad t_{\mathcal H}\colon A \to {\mathcal H}, \quad a \mapsto 1 \otimes a; \\& \Delta_{\mathcal H} \colon {\mathcal H} \to {\mathcal H} \otimes_{A} {\mathcal H}, \quad (a \otimes b)X \mapsto (a \otimes 1)X \otimes_{A} (1\otimes b)X; \\& \kern50pt \varepsilon_{\mathcal H}\colon {\mathcal H} \to A, \quad (a \otimes b)X \mapsto ab; \\&\kern2pt\begin{aligned} \beta_{\mathcal H}\colon {{\mathcal H}}{}_{t} \otimes_{A} {}_{t} {{\mathcal H}} & \to {{\mathcal H}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}}, \\ (a \otimes b)X^{n} \otimes_{A} (c \otimes d)X^{m} & \mapsto (a \otimes 1) X^{n} \otimes_{A} (c \otimes bd)X^{n+m}. \end{aligned} \end{align*} $$
$$ \begin{align*} & \kern6pt s_{\mathcal H}\colon A \to {\mathcal H}, \quad a \mapsto a \otimes 1; \qquad t_{\mathcal H}\colon A \to {\mathcal H}, \quad a \mapsto 1 \otimes a; \\& \Delta_{\mathcal H} \colon {\mathcal H} \to {\mathcal H} \otimes_{A} {\mathcal H}, \quad (a \otimes b)X \mapsto (a \otimes 1)X \otimes_{A} (1\otimes b)X; \\& \kern50pt \varepsilon_{\mathcal H}\colon {\mathcal H} \to A, \quad (a \otimes b)X \mapsto ab; \\&\kern2pt\begin{aligned} \beta_{\mathcal H}\colon {{\mathcal H}}{}_{t} \otimes_{A} {}_{t} {{\mathcal H}} & \to {{\mathcal H}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}}, \\ (a \otimes b)X^{n} \otimes_{A} (c \otimes d)X^{m} & \mapsto (a \otimes 1) X^{n} \otimes_{A} (c \otimes bd)X^{n+m}. \end{aligned} \end{align*} $$
As before, being
![]() ${\mathcal H}$
a commutative Hopf algebroid, it admits an antipode as well
${\mathcal H}$
a commutative Hopf algebroid, it admits an antipode as well
such that
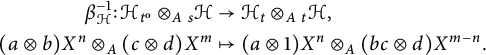 $$ \begin{align*} \beta_{\mathcal H}^{-1}\colon {{\mathcal H}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}} & \to {{\mathcal H}}{}_{t} \otimes_{A} {}_{t} {{\mathcal H}}, \\ (a \otimes b)X^{n} \otimes_{A} (c \otimes d)X^{m} & \mapsto (a \otimes 1)X^{n} \otimes_{A} (bc \otimes d)X^{m-n}. \end{align*} $$
$$ \begin{align*} \beta_{\mathcal H}^{-1}\colon {{\mathcal H}}{}_{t^{\mathrm{o}}} \otimes_{A} {}_{s} {{{\mathcal H}}} & \to {{\mathcal H}}{}_{t} \otimes_{A} {}_{t} {{\mathcal H}}, \\ (a \otimes b)X^{n} \otimes_{A} (c \otimes d)X^{m} & \mapsto (a \otimes 1)X^{n} \otimes_{A} (bc \otimes d)X^{m-n}. \end{align*} $$
Observe also that
![]() $B^+ = B\cdot \left \{ s(a) - t(a) \mid a \in A \right \} \oplus B\cdot (1-X)$
: on the one hand, by [Reference Saracco32, Proposition 4.3], we know that
$B^+ = B\cdot \left \{ s(a) - t(a) \mid a \in A \right \} \oplus B\cdot (1-X)$
: on the one hand, by [Reference Saracco32, Proposition 4.3], we know that
![]() $\left \{ s(a) - t(a) \mid a \in A \right \} = \textsf {Prim}(B) \subseteq \ker (\varepsilon _B)$
and since
$\left \{ s(a) - t(a) \mid a \in A \right \} = \textsf {Prim}(B) \subseteq \ker (\varepsilon _B)$
and since
![]() $1 - X$
is
$1 - X$
is
![]() $(1,X)$
-skew primitive, it is in
$(1,X)$
-skew primitive, it is in
![]() $\ker (\varepsilon _B)$
too. On the other hand, the composition
$\ker (\varepsilon _B)$
too. On the other hand, the composition
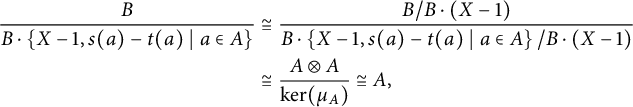 $$ \begin{align*} \frac{B}{B\cdot \left\{ X-1, s(a) - t(a) \mid a \in A \right\}} & \cong \frac{B/B\cdot (X-1)}{B\cdot \left\{ X-1, s(a) - t(a) \mid a \in A \right\}/B\cdot ( X-1)}\\ & \cong \frac{A \otimes A}{\ker(\mu_A)} \cong A, \end{align*} $$
$$ \begin{align*} \frac{B}{B\cdot \left\{ X-1, s(a) - t(a) \mid a \in A \right\}} & \cong \frac{B/B\cdot (X-1)}{B\cdot \left\{ X-1, s(a) - t(a) \mid a \in A \right\}/B\cdot ( X-1)}\\ & \cong \frac{A \otimes A}{\ker(\mu_A)} \cong A, \end{align*} $$
where
![]() $\mu _A$
is the multiplication of A, coincides exactly with the morphism induced by
$\mu _A$
is the multiplication of A, coincides exactly with the morphism induced by
![]() $\varepsilon _B$
.
$\varepsilon _B$
.
Now, both
![]() ${}_{s} {{B}}$
and
${}_{s} {{B}}$
and
![]() ${}_{s} {{{\mathcal H}}}$
are (faithfully) flat over A and B is a right
${}_{s} {{{\mathcal H}}}$
are (faithfully) flat over A and B is a right
![]() ${\mathcal H}$
-comodule A-subring of
${\mathcal H}$
-comodule A-subring of
![]() ${\mathcal H}$
via t. Furthermore, for all
${\mathcal H}$
via t. Furthermore, for all
![]() $a,b \in A$
,
$a,b \in A$
,
![]() $n \in {\mathbb {N}}$
, we have
$n \in {\mathbb {N}}$
, we have
However,
![]() ${\mathcal H}$
cannot be pure over B since
${\mathcal H}$
cannot be pure over B since
![]() ${\mathcal H} = S^{-1}B$
for
${\mathcal H} = S^{-1}B$
for
![]() $S = \left \{X^n \mid n \in \mathbb {N}\right \}$
. To check this, it is enough to tensor the injection
$S = \left \{X^n \mid n \in \mathbb {N}\right \}$
. To check this, it is enough to tensor the injection
![]() $B \hookrightarrow {\mathcal H}$
by
$B \hookrightarrow {\mathcal H}$
by
![]() $A \otimes A \cong B/\langle X\rangle $
over B on the right:
$A \otimes A \cong B/\langle X\rangle $
over B on the right:
![]() $B \otimes _{B} (A \otimes A) \cong A \otimes A$
, while
$B \otimes _{B} (A \otimes A) \cong A \otimes A$
, while
![]() ${\mathcal H} \otimes _{B} (A \otimes A) = 0$
.
${\mathcal H} \otimes _{B} (A \otimes A) = 0$
.
To show how Theorem 3.13 fails, consider a generic element
 $$ \begin{align*}h = \sum_{\substack{z \in \mathbb{Z} \\ i \in I}} \left(a_{z,i} \otimes b_{z,i}\right)X^z \in (A \otimes A)[X^{\pm 1}]\end{align*} $$
$$ \begin{align*}h = \sum_{\substack{z \in \mathbb{Z} \\ i \in I}} \left(a_{z,i} \otimes b_{z,i}\right)X^z \in (A \otimes A)[X^{\pm 1}]\end{align*} $$
and denote by
![]() $\textsf {supp}(h)$
the set of the
$\textsf {supp}(h)$
the set of the
![]() $z \in \mathbb {Z}$
such that
$z \in \mathbb {Z}$
such that
![]() $X^z$
appears with nonzero coefficient. Then notice that if
$X^z$
appears with nonzero coefficient. Then notice that if
![]() $z \geq 0$
, then
$z \geq 0$
, then
![]() $X^z + {\mathcal H} B^+ = 1 + {\mathcal H} B^+$
because
$X^z + {\mathcal H} B^+ = 1 + {\mathcal H} B^+$
because
and if
![]() $z < 0$
, then
$z < 0$
, then
![]() $1/X^{|z|} + {\mathcal H} B^+ = 1 + {\mathcal H} B^+$
too because
$1/X^{|z|} + {\mathcal H} B^+ = 1 + {\mathcal H} B^+$
too because
Therefore,
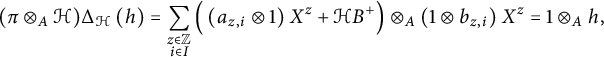 $$ \begin{align*} (\pi \otimes_{A} {\mathcal H})\Delta_{\mathcal H}\left(h\right) = \sum_{\substack{z \in \mathbb{Z} \\ i \in I}} \Big(\left(a_{z,i} \otimes 1\right)X^z + {\mathcal H} B^+\Big) \otimes_{A} \left(1 \otimes b_{z,i}\right)X^z = 1 \otimes_{A} h, \end{align*} $$
$$ \begin{align*} (\pi \otimes_{A} {\mathcal H})\Delta_{\mathcal H}\left(h\right) = \sum_{\substack{z \in \mathbb{Z} \\ i \in I}} \Big(\left(a_{z,i} \otimes 1\right)X^z + {\mathcal H} B^+\Big) \otimes_{A} \left(1 \otimes b_{z,i}\right)X^z = 1 \otimes_{A} h, \end{align*} $$
or, equivalently,
![]() ${\mathcal H} = {\mathcal H}^{\mathrm {co}\frac {{\mathcal H}}{{\mathcal H} B^+}}$
.
${\mathcal H} = {\mathcal H}^{\mathrm {co}\frac {{\mathcal H}}{{\mathcal H} B^+}}$
.
4 Affine groupoids and commutative Hopf algebroids
We discuss here the specific case of the aforementioned correspondence for commutative Hopf algebroids, and we apply it to the study of affine groupoids.
4.1 Preliminaries on groupoids and normal subgroupoids
4.1.1 Groupoids and subgroupoids
Recall, for instance, from [Reference Mackenzie26, Chapter I, Definition 1.1], that a groupoid is a small category (i.e., the class of objects is a set) in which every arrow is invertible. We will usually denote a groupoid
![]() $\mathscr {G}$
by a pair
$\mathscr {G}$
by a pair
![]() $\big (\mathscr {G}_0,\mathscr {G}_1\big )$
of sets: the set of objects
$\big (\mathscr {G}_0,\mathscr {G}_1\big )$
of sets: the set of objects
![]() $\mathscr {G}_0$
and the set of arrows
$\mathscr {G}_0$
and the set of arrows
![]() $\mathscr {G}_1$
. A groupoid
$\mathscr {G}_1$
. A groupoid
![]() $\big (\mathscr {G}_0,\mathscr {G}_1\big )$
always comes with an (understood) family of maps
$\big (\mathscr {G}_0,\mathscr {G}_1\big )$
always comes with an (understood) family of maps
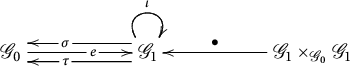
satisfying the expected, reasonable, compatibility conditions. For the sake of simplicity, one often denotes a composition
![]() $\bullet (f,g)$
by simple juxtaposition
$\bullet (f,g)$
by simple juxtaposition
![]() $fg$
. A subgroupoid of a groupoid
$fg$
. A subgroupoid of a groupoid
![]() $\mathscr {G}$
is a subcategory which is also a groupoid.
$\mathscr {G}$
is a subcategory which is also a groupoid.
For a given groupoid
![]() $\mathscr {G} = \big (\mathscr {G}_0, \mathscr {G}_1\big )$
, the associated isotropy groupoid (also called inner subgroupoid in [Reference Mackenzie26, Chapter I, Definition 2.4]) is the subgroupoid
$\mathscr {G} = \big (\mathscr {G}_0, \mathscr {G}_1\big )$
, the associated isotropy groupoid (also called inner subgroupoid in [Reference Mackenzie26, Chapter I, Definition 2.4]) is the subgroupoid
, where
![]() $\mathscr {G}_x$
is the isotropy group of
$\mathscr {G}_x$
is the isotropy group of
![]() $x \in \mathscr {G}_0$
, that is to say,
$x \in \mathscr {G}_0$
, that is to say,
In the isotropy groupoid, the source and the target coincide and we denote them simply by
![]() $o\colon \mathscr {G}^{{(i)}} \to \mathscr {G}_0, g \mapsto \sigma (g) = \tau (g)$
. Moreover, there is a canonical morphism of groupoids
$o\colon \mathscr {G}^{{(i)}} \to \mathscr {G}_0, g \mapsto \sigma (g) = \tau (g)$
. Moreover, there is a canonical morphism of groupoids
![]() $\mathscr {G}^{{(i)}} \to \mathscr {G}$
(the inclusion).
$\mathscr {G}^{{(i)}} \to \mathscr {G}$
(the inclusion).
4.1.2 Groupoid actions and normal subgroupoids
Recall that a left
![]() $\mathscr {G}$
-action of a groupoid
$\mathscr {G}$
-action of a groupoid
![]() $\mathscr {G}$
on a set N consists of two maps
$\mathscr {G}$
on a set N consists of two maps
![]() $\rho \colon N \to \mathscr {G}_{0}$
and
$\rho \colon N \to \mathscr {G}_{0}$
and
, satisfying
for all
![]() $g , g'\in \mathscr {G}_1$
and
$g , g'\in \mathscr {G}_1$
and
![]() $n \in N$
(see [Reference Mackenzie26, Definition 4.1] for the topological analog and [Reference Mackenzie27, Definition 1.6.1] for the differential one). Given a left
$n \in N$
(see [Reference Mackenzie26, Definition 4.1] for the topological analog and [Reference Mackenzie27, Definition 1.6.1] for the differential one). Given a left
![]() $\mathscr {G}$
-action on N, one can consider the left translation groupoid
$\mathscr {G}$
-action on N, one can consider the left translation groupoid
with
as set of arrows and N as set of objects. This is the so-called semi-direct product groupoid. The source and the target of this groupoid are given by
The identity of
![]() $n \in N$
is
$n \in N$
is
![]() $e_n = (e_{\rho (n)}, n)$
. The composition is given by
$e_n = (e_{\rho (n)}, n)$
. The composition is given by
Obviously, the pair
defines a morphism of groupoids.
Example 4.1 (Action groupoid)
Any group G can be considered as a groupoid by taking
![]() $\mathscr {G}_1 = G$
and
$\mathscr {G}_1 = G$
and
![]() $\mathscr {G}_0=\{*\}$
(the singleton). If X is a set with an action
$\mathscr {G}_0=\{*\}$
(the singleton). If X is a set with an action
![]() $G \times X \to X$
of G, then one can define the so-called action groupoid. It is constructed over
$G \times X \to X$
of G, then one can define the so-called action groupoid. It is constructed over
![]() and
and
![]() . Source and target are provided by
. Source and target are provided by
![]() and
and
![]() for all
for all
![]() $x \in X$
and
$x \in X$
and
![]() $g \in G$
. The identity map sends x to
$g \in G$
. The identity map sends x to
![]() $(e, x)$
, where e is the neutral element of G. The composition law is given by
$(e, x)$
, where e is the neutral element of G. The composition law is given by
![]() whenever
whenever
![]() ${y = g \cdot x}$
, and the inverse is defined by
${y = g \cdot x}$
, and the inverse is defined by
![]() . Clearly, the pair of maps
. Clearly, the pair of maps
![]() $(\mathrm {pr}_1, *) \colon (\mathscr {G}_1, \mathscr {G}_0) \to (G, \{*\})$
defines a morphism of groupoids.
$(\mathrm {pr}_1, *) \colon (\mathscr {G}_1, \mathscr {G}_0) \to (G, \{*\})$
defines a morphism of groupoids.
As for groups, conjugation in
![]() $\mathscr {G}$
can be seen as an action of
$\mathscr {G}$
can be seen as an action of
![]() $\mathscr {G}$
on the underlying set of arrow of its isotropy groupoid
$\mathscr {G}$
on the underlying set of arrow of its isotropy groupoid
![]() $\mathscr {G}^{{(i)}}$
. In detail, define the map
$\mathscr {G}^{{(i)}}$
. In detail, define the map
![]() acting as
acting as
![]() $\operatorname {Ad}(g,f) = gfg^{-1}$
. One can show that this defines an action, called the adjoint action, so that
$\operatorname {Ad}(g,f) = gfg^{-1}$
. One can show that this defines an action, called the adjoint action, so that
![]() $\mathscr {G}^{(i)}_1$
becomes a left
$\mathscr {G}^{(i)}_1$
becomes a left
![]() $\mathscr {G}$
-set.
$\mathscr {G}$
-set.
A normal subgroupoid of
![]() $\mathscr {G}$
is a subgroupoid
$\mathscr {G}$
is a subgroupoid
![]() $\mathscr {N} \hookrightarrow \mathscr {G}$
such that:
$\mathscr {N} \hookrightarrow \mathscr {G}$
such that:
-
(NG0)
 $\mathscr {N}_0 =\mathscr {G}_0$
(i.e.,
$\mathscr {N}_0 =\mathscr {G}_0$
(i.e.,
 $\mathscr {N}$
is wide in the sense of [Reference Mackenzie26, Chapter I, Definition 2.4]);
$\mathscr {N}$
is wide in the sense of [Reference Mackenzie26, Chapter I, Definition 2.4]); -
(NG1)
 $\mathscr {N}_1(x,y)= \emptyset $
, for all
$\mathscr {N}_1(x,y)= \emptyset $
, for all
 $x \neq y $
in
$x \neq y $
in
 $\mathscr {N}_0$
(that is,
$\mathscr {N}_0$
(that is,
 $\mathscr {N}$
is a subgroupoid of
$\mathscr {N}$
is a subgroupoid of
 $\mathscr {G}^{(i)}$
);
$\mathscr {G}^{(i)}$
); -
(NG2) for every
 $g \in \mathscr {G}_1$
, we have
$g \in \mathscr {G}_1$
, we have  $$ \begin{align*} \operatorname{Ad}(g)\Big(\mathscr{N}_1\big(\sigma(g), \sigma(g)\big)\Big) \subseteq \mathscr{N}_1(\tau(g),\tau(g)) \end{align*} $$
$$ \begin{align*} \operatorname{Ad}(g)\Big(\mathscr{N}_1\big(\sigma(g), \sigma(g)\big)\Big) \subseteq \mathscr{N}_1(\tau(g),\tau(g)) \end{align*} $$
as subgroups of
 $\mathscr {G}_1\big (\tau (g),\tau (g)\big )$
, where
$\mathscr {G}_1\big (\tau (g),\tau (g)\big )$
, where
 $\operatorname {Ad}(g)(f)=\operatorname {Ad}(g,f)$
for all f with
$\operatorname {Ad}(g)(f)=\operatorname {Ad}(g,f)$
for all f with
 $\sigma (f) = \tau (f) = \sigma (g)$
.
$\sigma (f) = \tau (f) = \sigma (g)$
.
Equivalently, a subgroupoid
![]() $\mathscr {N} \hookrightarrow \mathscr {G}$
is normal (in the above sense) if and only if
$\mathscr {N} \hookrightarrow \mathscr {G}$
is normal (in the above sense) if and only if
![]() $\mathscr {N}$
is a subgroupoid of
$\mathscr {N}$
is a subgroupoid of
![]() $\mathscr {G}^{(i)}$
,
$\mathscr {G}^{(i)}$
,
is non empty, and
![]() $g\mathscr {N} g^{-1} \subseteq \mathscr {N}$
for all
$g\mathscr {N} g^{-1} \subseteq \mathscr {N}$
for all
![]() $g \in \mathscr {G}_1$
(see [Reference Paques and Tamusiunas29, Lemma 3.1]). In particular, we denote again by
$g \in \mathscr {G}_1$
(see [Reference Paques and Tamusiunas29, Lemma 3.1]). In particular, we denote again by
![]() $o \colon \mathscr {N} \to \mathscr {N}_0, n \mapsto \sigma (n) = \tau (n)$
, the common source and target of a normal subgroupoid.
$o \colon \mathscr {N} \to \mathscr {N}_0, n \mapsto \sigma (n) = \tau (n)$
, the common source and target of a normal subgroupoid.
Remark 4.2 Condition (NG1), which explicitly appears in [Reference Brown5, Section 1] and [Reference Mackenzie27, Definition 2.2.1], does not appear in [Reference Mackenzie26, Chapter I, Definition 2.5] or [Reference Paques and Tamusiunas29, Section 3]. However, as observed in [Reference Mackenzie26, p. 8], whether or not a subgroupoid is normal depends only on those of its elements which lie in its isotropy groupoid.
The fact that normal subgroups can be characterized as the invariant subgroups under the adjoint action can be extended to the groupoids context, as the following lemma states.
Lemma 4.3 Let
![]() $\mathscr {G}$
be a groupoid, and let
$\mathscr {G}$
be a groupoid, and let
![]() $\mathscr {N} \hookrightarrow \mathscr {G}$
be a subcategory with
$\mathscr {N} \hookrightarrow \mathscr {G}$
be a subcategory with
![]() $\mathscr {N}_0=\mathscr {G}_0$
. Then
$\mathscr {N}_0=\mathscr {G}_0$
. Then
![]() $\mathscr {N}$
is a normal subgroupoid if and only if
$\mathscr {N}$
is a normal subgroupoid if and only if
![]() $\mathscr {N}_1$
is a
$\mathscr {N}_1$
is a
![]() $\mathscr {G}$
-equivariant subset of
$\mathscr {G}$
-equivariant subset of
![]() $\mathscr {G}^{(i)}_1$
.
$\mathscr {G}^{(i)}_1$
.
Proof Straightforward.
4.1.3 The orbit space
Let
![]() $\mathscr {G}$
be a groupoid, and let N be a left
$\mathscr {G}$
be a groupoid, and let N be a left
![]() $\mathscr {G}$
-set. For
$\mathscr {G}$
-set. For
![]() $n \in N$
, one defines the orbit of n under
$n \in N$
, one defines the orbit of n under
![]() $\mathscr {G}$
to be
$\mathscr {G}$
to be
(see, e.g., [Reference Mackenzie26, Definition 4.1]). This induces an equivalence relation on N given by
The quotient space with respect to this relation, called the orbit space of N with respect to the action of
![]() $\mathscr {G}$
, is denoted by
$\mathscr {G}$
, is denoted by
![]() $N/\mathscr {G}$
, and its elements are the orbits
$N/\mathscr {G}$
, and its elements are the orbits
![]() $\mathscr {G} n$
for
$\mathscr {G} n$
for
![]() $n \in N$
. See, for instance, [Reference Goehle20, Definition 1.67]. In particular, given a groupoid
$n \in N$
. See, for instance, [Reference Goehle20, Definition 1.67]. In particular, given a groupoid
![]() $\mathscr {G}$
, one can consider the orbit equivalence relation on
$\mathscr {G}$
, one can consider the orbit equivalence relation on
![]() $\mathscr {G}_0$
with respect to the action of
$\mathscr {G}_0$
with respect to the action of
![]() $\mathscr {G}$
given by
$\mathscr {G}$
given by
In this case,
![]() $x \sim y$
if and only if there exists a
$x \sim y$
if and only if there exists a
![]() $g \in \mathscr {G}_1$
such that
$g \in \mathscr {G}_1$
such that
![]() $\sigma (g) = x$
and
$\sigma (g) = x$
and
![]() $\tau (g) = y$
. The orbit of
$\tau (g) = y$
. The orbit of
![]() $x \in \mathscr {G}_0$
is
$x \in \mathscr {G}_0$
is
The set of orbits, called the orbit space, of
![]() $\mathscr {G}$
is the quotient set
$\mathscr {G}$
is the quotient set
![]() $\mathscr {G}_{0}/\sim $
, which is often denoted by
$\mathscr {G}_{0}/\sim $
, which is often denoted by
![]() $\mathscr {G}_{0}/\mathscr {G}$
. For further details, we refer the reader to [Reference Goehle20, Section 1.2].
$\mathscr {G}_{0}/\mathscr {G}$
. For further details, we refer the reader to [Reference Goehle20, Section 1.2].
Remark 4.4 For a left
![]() $\mathscr {G}$
-set N, the orbit space
$\mathscr {G}$
-set N, the orbit space
![]() $N/\mathscr {G}$
of N with respect to the action of
$N/\mathscr {G}$
of N with respect to the action of
![]() $\mathscr {G}$
can also be described as the orbit space of the left translation groupoid
$\mathscr {G}$
can also be described as the orbit space of the left translation groupoid
. In fact, for
![]() $p \in N$
, we have
$p \in N$
, we have
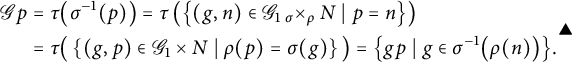
Now, we will use this notion to describe the quotient groupoid by a normal subgroupoid as in the classical case of groups. Let us consider a normal subgroupoid
![]() $\mathscr {N} \hookrightarrow \mathscr {G}$
. It is clear that
$\mathscr {N} \hookrightarrow \mathscr {G}$
. It is clear that
![]() $(\mathscr {G}_1, \tau )$
is a left
$(\mathscr {G}_1, \tau )$
is a left
![]() $\mathscr {N}$
-set via the left action
$\mathscr {N}$
-set via the left action
We denote by
![]() $\mathscr {G}_1/\mathscr {N}$
the orbit space of this action (or, equivalently, the orbit space of the associated left translation groupoid
$\mathscr {G}_1/\mathscr {N}$
the orbit space of this action (or, equivalently, the orbit space of the associated left translation groupoid
![]() ) and call it the quotient groupoid (see [Reference Mackenzie26, pp. 9–10]). As a matter of description, the equivalence class of a given arrow
) and call it the quotient groupoid (see [Reference Mackenzie26, pp. 9–10]). As a matter of description, the equivalence class of a given arrow
![]() $g \in \mathscr {G}_1$
is a “flower with stalk at g”:
$g \in \mathscr {G}_1$
is a “flower with stalk at g”:
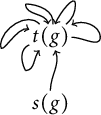
Two arrows are equivalent if they “support the same flower.” The action (4.1) is in fact a left one. There is also a right
![]() $\mathscr {N}$
-action on
$\mathscr {N}$
-action on
![]() $(\mathscr {G}_1, \sigma )$
, which leads to the groupoid
$(\mathscr {G}_1, \sigma )$
, which leads to the groupoid
![]() and, in principle, to another orbit space
and, in principle, to another orbit space
![]() $\mathscr {G}_1/\mathscr {N}$
. It is easy to verify that the two orbit spaces coincide, since
$\mathscr {G}_1/\mathscr {N}$
. It is easy to verify that the two orbit spaces coincide, since
![]() $\mathscr {N}$
is normal. The following result is expected (see also [Reference Mackenzie26, pp. 9–10]).
$\mathscr {N}$
is normal. The following result is expected (see also [Reference Mackenzie26, pp. 9–10]).
Lemma 4.5 ([Reference Barbarán Sánchez and El Kaoutit2, Proposition 2.16])
Let
![]() $\mathscr {N} \hookrightarrow \mathscr {G}$
be a normal subgroupoid. Then
$\mathscr {N} \hookrightarrow \mathscr {G}$
be a normal subgroupoid. Then
have a structure of groupoid such that there is a chain of morphisms
Furthermore, any morphism
![]() $\mathscr {G} \to \mathscr {H}$
whose kernel contains
$\mathscr {G} \to \mathscr {H}$
whose kernel contains
![]() $\mathscr {N}$
factors through
$\mathscr {N}$
factors through
![]() $\varpi $
.
$\varpi $
.
4.2 Commutative Hopf algebroids
In view of the easier expression of commutative Hopf algebroids with respect to general bialgebroids and Hopf algebroids, we begin by recalling explicitly their definition, both for the convenience of the reader and for future reference.
As a matter of notation, if A and R are commutative
![]() $\Bbbk $
-algebras, then we will write
$\Bbbk $
-algebras, then we will write
![]() $A(R)$
for
$A(R)$
for
![]() $\mathrm {CAlg}_{\Bbbk }(A,R)$
.
$\mathrm {CAlg}_{\Bbbk }(A,R)$
.
4.2.1 Commutative Hopf algebroids and Hopf ideals
Definition 4.1 A commutative Hopf algebroid is a cogroupoid object in the category
![]() $\mathrm {CAlg}_{\Bbbk }$
of commutative algebras (see, e.g., [Reference Ravenel31]). Thus, a commutative Hopf algebroid consists of a pair of commutative
$\mathrm {CAlg}_{\Bbbk }$
of commutative algebras (see, e.g., [Reference Ravenel31]). Thus, a commutative Hopf algebroid consists of a pair of commutative
![]() $\Bbbk $
-algebras
$\Bbbk $
-algebras
![]() $\left ( A,\mathcal {H}\right ) $
together with a diagram of algebra maps
$\left ( A,\mathcal {H}\right ) $
together with a diagram of algebra maps
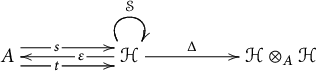
(where the A-bimodule structure on
![]() ${\mathcal H}$
used to perform the tensor product is
${\mathcal H}$
used to perform the tensor product is
![]() ${}_{s} {{\mathcal H}}{}_{t}$
) such that:
${}_{s} {{\mathcal H}}{}_{t}$
) such that:
-
(CH1) The datum
 $({\mathcal H}, \Delta , \varepsilon )$
is an A-coring structure on
$({\mathcal H}, \Delta , \varepsilon )$
is an A-coring structure on
 ${}_{s} {{\mathcal H}}{}_{t}$
. At the level of groupoids, this encodes a unitary and associative composition law between arrows.
${}_{s} {{\mathcal H}}{}_{t}$
. At the level of groupoids, this encodes a unitary and associative composition law between arrows. -
(CH2) The antipode
 ${\mathcal S}$
satisfies
${\mathcal S}$
satisfies
 ${\mathcal S} \circ s=t$
,
${\mathcal S} \circ s=t$
,
 ${\mathcal S} \circ t = s$
and
${\mathcal S} \circ t = s$
and
 ${\mathcal S}^2=\operatorname {Id}_{{\mathcal H}}$
, which encode the fact that the inverse of an arrow interchanges source and target and that the inverse of the inverse is the original arrow.
${\mathcal S}^2=\operatorname {Id}_{{\mathcal H}}$
, which encode the fact that the inverse of an arrow interchanges source and target and that the inverse of the inverse is the original arrow. -
(CH3) The antipode also satisfies
 $\sum {\mathcal S}(u_1)u_2=(t\circ \varepsilon )(u)$
and
$\sum {\mathcal S}(u_1)u_2=(t\circ \varepsilon )(u)$
and
 $\sum u_1{\mathcal S}(u_2)= (s\circ \varepsilon )(u)$
, which encode the fact that the composition of a morphism with its inverse on either side gives an identity morphism.
$\sum u_1{\mathcal S}(u_2)= (s\circ \varepsilon )(u)$
, which encode the fact that the composition of a morphism with its inverse on either side gives an identity morphism.
In particular, the inverse of the Hopf–Galois map
is provided by
Thus, explicitly,
A morphism of commutative Hopf algebroids
![]() $\boldsymbol {\phi }\colon (A,{\mathcal H}) \to (B,{\mathcal K})$
is a pair of algebra maps
$\boldsymbol {\phi }\colon (A,{\mathcal H}) \to (B,{\mathcal K})$
is a pair of algebra maps
![]() $\left ( \phi _{{0}} \colon A \to B,\phi _{{1}} \colon {\mathcal H} \to {\mathcal K}\right )$
such that
$\left ( \phi _{{0}} \colon A \to B,\phi _{{1}} \colon {\mathcal H} \to {\mathcal K}\right )$
such that
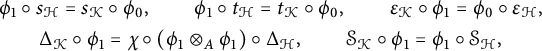 $$ \begin{gather*} \phi _{1}\circ s_{\mathcal H} = s_{\mathcal K} \circ \phi _{0}, \qquad \phi _{1}\circ t_{\mathcal H} = t_{\mathcal K} \circ \phi_{0}, \qquad \varepsilon_{\mathcal K} \circ \phi _{1} = \phi _{0} \circ \varepsilon_{\mathcal H} , \\ \Delta_{\mathcal K} \circ \phi _{1} =\chi \circ \left( \phi _{1}\otimes _{A}\phi_{1}\right) \circ \Delta_{\mathcal H} , \qquad {\mathcal S}_{\mathcal K} \circ \phi _{1} =\phi _{1} \circ {\mathcal S}_{\mathcal H}, \end{gather*} $$
$$ \begin{gather*} \phi _{1}\circ s_{\mathcal H} = s_{\mathcal K} \circ \phi _{0}, \qquad \phi _{1}\circ t_{\mathcal H} = t_{\mathcal K} \circ \phi_{0}, \qquad \varepsilon_{\mathcal K} \circ \phi _{1} = \phi _{0} \circ \varepsilon_{\mathcal H} , \\ \Delta_{\mathcal K} \circ \phi _{1} =\chi \circ \left( \phi _{1}\otimes _{A}\phi_{1}\right) \circ \Delta_{\mathcal H} , \qquad {\mathcal S}_{\mathcal K} \circ \phi _{1} =\phi _{1} \circ {\mathcal S}_{\mathcal H}, \end{gather*} $$
where
![]() $\chi \colon {\mathcal K} \otimes _{A} {\mathcal K} \rightarrow {\mathcal K} \otimes _{B} {\mathcal K}$
is the obvious projection induced by
$\chi \colon {\mathcal K} \otimes _{A} {\mathcal K} \rightarrow {\mathcal K} \otimes _{B} {\mathcal K}$
is the obvious projection induced by
![]() $\phi _0$
, that is,
$\phi _0$
, that is,
![]() $\chi \left (k\otimes _{A}k'\right ) =k\otimes _{B}k'$
. If
$\chi \left (k\otimes _{A}k'\right ) =k\otimes _{B}k'$
. If
![]() $A = B$
and
$A = B$
and
![]() $\phi _0 = \operatorname {Id}_A$
, then we say that
$\phi _0 = \operatorname {Id}_A$
, then we say that
![]() $\phi _1 : {\mathcal H} \to {\mathcal K}$
is a morphism of Hopf algebroids over A.
$\phi _1 : {\mathcal H} \to {\mathcal K}$
is a morphism of Hopf algebroids over A.
Remark 4.6 Let
![]() $(A, {\mathcal H})$
be commutative Hopf algebroid such that
$(A, {\mathcal H})$
be commutative Hopf algebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is flat as an A-module (i.e., the extension
${}_{s} {{{\mathcal H}}}$
is flat as an A-module (i.e., the extension
![]() $s \colon A \to {\mathcal H}$
is flat). In this case,
$s \colon A \to {\mathcal H}$
is flat). In this case,
![]() $t \colon A \to {\mathcal H}$
is also flat due to the isomorphism given by the antipode. Therefore, both extensions
$t \colon A \to {\mathcal H}$
is also flat due to the isomorphism given by the antipode. Therefore, both extensions
![]() $s $
and
$s $
and
![]() $t $
are faithfully flat since both are (left) split morphisms of modules over the base algebra.
$t $
are faithfully flat since both are (left) split morphisms of modules over the base algebra.
Similarly to how commutative Hopf algebras over a field
![]() $\Bbbk $
are the same thing as affine
$\Bbbk $
are the same thing as affine
![]() $\Bbbk $
-group schemes (that is, representable presheaves of groups on
$\Bbbk $
-group schemes (that is, representable presheaves of groups on
![]() $\mathrm {Aff}_{\Bbbk } = \mathrm {CAlg}_{\Bbbk }^{\mathrm {op}}$
, the opposite of the category of commutative
$\mathrm {Aff}_{\Bbbk } = \mathrm {CAlg}_{\Bbbk }^{\mathrm {op}}$
, the opposite of the category of commutative
![]() $\Bbbk $
-algebras), commutative Hopf algebroids are the same thing as affine groupoid schemes (that is, representable presheaves of groupoids on
$\Bbbk $
-algebras), commutative Hopf algebroids are the same thing as affine groupoid schemes (that is, representable presheaves of groupoids on
![]() $\mathrm {Aff}_{\Bbbk }$
). Precisely, given a commutative Hopf algebroid
$\mathrm {Aff}_{\Bbbk }$
). Precisely, given a commutative Hopf algebroid
![]() $(A, {\mathcal H})$
and a commutative
$(A, {\mathcal H})$
and a commutative
![]() $\Bbbk $
-algebra R, we have a groupoid
$\Bbbk $
-algebra R, we have a groupoid
![]() by reversing the structures of
by reversing the structures of
![]() $(A,{\mathcal H})$
. We will often adopt this point of view, and we will denote by
$(A,{\mathcal H})$
. We will often adopt this point of view, and we will denote by
![]() $\mathscr {G}_{(A,{\mathcal H})} = \big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
the groupoid scheme defined by
$\mathscr {G}_{(A,{\mathcal H})} = \big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
the groupoid scheme defined by
![]() $(A,{\mathcal H})$
, that is to say,
$(A,{\mathcal H})$
, that is to say,
in order to stress the groupoid structure on the pair
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
. Observe that, under this perspective,
$\big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
. Observe that, under this perspective,
for all
![]() ,
,
![]() $h \in {\mathcal H}$
and R in
$h \in {\mathcal H}$
and R in
![]() $\mathrm {CAlg}_{\Bbbk }$
.
$\mathrm {CAlg}_{\Bbbk }$
.
Remark 4.7 In particular,
![]() $\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{\mathcal H}(\Bbbk )\big )$
will be called an affine
$\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{\mathcal H}(\Bbbk )\big )$
will be called an affine
![]() $\Bbbk $
-groupoid, and when
$\Bbbk $
-groupoid, and when
![]() $A,{\mathcal H}$
are finitely generated and reduced, then it will be called an affine algebraic
$A,{\mathcal H}$
are finitely generated and reduced, then it will be called an affine algebraic
![]() $\Bbbk $
-groupoid. Suppose that
$\Bbbk $
-groupoid. Suppose that
![]() $\Bbbk $
is algebraically closed. Denote by
$\Bbbk $
is algebraically closed. Denote by
![]() $\mathrm {Aff}_1:\mathrm {CAlg}_{\Bbbk } \to \mathrm {Set}$
the affine scheme represented by the polynomial algebra
$\mathrm {Aff}_1:\mathrm {CAlg}_{\Bbbk } \to \mathrm {Set}$
the affine scheme represented by the polynomial algebra
![]() $\Bbbk [T]$
and by
$\Bbbk [T]$
and by
![]() $\operatorname {Var}_{\Bbbk }$
the category of affine
$\operatorname {Var}_{\Bbbk }$
the category of affine
![]() $\Bbbk $
-varieties (i.e., the category whose objects are
$\Bbbk $
-varieties (i.e., the category whose objects are
![]() $\mathrm {CAlg}_{\Bbbk }(R,\Bbbk )$
for R a finitely generated and reduced commutative algebra and whose morphisms are given by precomposition by morphisms in
$\mathrm {CAlg}_{\Bbbk }(R,\Bbbk )$
for R a finitely generated and reduced commutative algebra and whose morphisms are given by precomposition by morphisms in
![]() $\mathrm {CAlg}_{\Bbbk }$
). Then
$\mathrm {CAlg}_{\Bbbk }$
). Then
 $$ \begin{gather*} (A,{\mathcal H}) \mapsto \big(\mathscr{G}_A(\Bbbk),\mathscr{G}_{\mathcal H}(\Bbbk)\big) \quad \text{and} \\ \big(\mathscr{G}_A(\Bbbk),\mathscr{G}_{\mathcal H}(\Bbbk)\big) \mapsto \Big(\operatorname{Var}_{\Bbbk}\big(\mathscr{G}_A(\Bbbk),\mathrm{Aff}_1(\Bbbk)\big),\operatorname{Var}_{\Bbbk}\big(\mathscr{G}_{\mathcal H}(\Bbbk),\mathrm{Aff}_1(\Bbbk)\big)\Big) \end{gather*} $$
$$ \begin{gather*} (A,{\mathcal H}) \mapsto \big(\mathscr{G}_A(\Bbbk),\mathscr{G}_{\mathcal H}(\Bbbk)\big) \quad \text{and} \\ \big(\mathscr{G}_A(\Bbbk),\mathscr{G}_{\mathcal H}(\Bbbk)\big) \mapsto \Big(\operatorname{Var}_{\Bbbk}\big(\mathscr{G}_A(\Bbbk),\mathrm{Aff}_1(\Bbbk)\big),\operatorname{Var}_{\Bbbk}\big(\mathscr{G}_{\mathcal H}(\Bbbk),\mathrm{Aff}_1(\Bbbk)\big)\Big) \end{gather*} $$
give an anti-equivalence between the category of affine (i.e., finitely generated, commutative, reduced) Hopf algebroids and the category of affine algebraic
![]() $\Bbbk $
-groupoids, where
$\Bbbk $
-groupoids, where
▲
Let
![]() $(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
be an affine groupoid scheme, and let
$(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
be an affine groupoid scheme, and let
![]() $I\subseteq {\mathcal H}$
be an ideal. Denote by
$I\subseteq {\mathcal H}$
be an ideal. Denote by
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
the canonical projection and by
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
the canonical projection and by
![]() $\pi ^*\colon \mathrm {CAlg}_{\Bbbk }({\mathcal H}/I,-) \to \mathrm {CAlg}_{\Bbbk }({\mathcal H},-)$
the natural transformation given by precomposition by
$\pi ^*\colon \mathrm {CAlg}_{\Bbbk }({\mathcal H}/I,-) \to \mathrm {CAlg}_{\Bbbk }({\mathcal H},-)$
the natural transformation given by precomposition by
![]() $\pi $
. We say that
$\pi $
. We say that
![]() $(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I})$
is a wide closed groupoid subscheme of
$(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I})$
is a wide closed groupoid subscheme of
![]() $(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
(or, simply, a wide closed subgroupoid or wide affine subgroupoid of
$(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
(or, simply, a wide closed subgroupoid or wide affine subgroupoid of
![]() $(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
) if
$(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
) if
![]() $(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I})$
is a groupoid itself and
$(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I})$
is a groupoid itself and
![]() $\pi ^*:\mathscr {G}_{{\mathcal H}/I} \hookrightarrow \mathscr {G}_{\mathcal H}$
induces a morphism of groupoids
$\pi ^*:\mathscr {G}_{{\mathcal H}/I} \hookrightarrow \mathscr {G}_{\mathcal H}$
induces a morphism of groupoids
![]() $(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}) \to (\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
. Since the structure maps of the commutative Hopf algebroid
$(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}) \to (\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
. Since the structure maps of the commutative Hopf algebroid
![]() ${\mathcal H}/I$
should be induced by the structure maps of
${\mathcal H}/I$
should be induced by the structure maps of
![]() ${\mathcal H}$
via
${\mathcal H}$
via
![]() $\pi $
,
$\pi $
,
![]() $(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I})$
is a wide subgroupoid of
$(\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I})$
is a wide subgroupoid of
![]() $(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
if and only if
$(\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
if and only if
![]() $(A,{\mathcal H}/I)$
is a commutative Hopf algebroid and
$(A,{\mathcal H}/I)$
is a commutative Hopf algebroid and
![]() $\pi :{\mathcal H} \to {\mathcal H}/I$
is a morphism of commutative Hopf algebroids, if and only if the ideal I satisfies:
$\pi :{\mathcal H} \to {\mathcal H}/I$
is a morphism of commutative Hopf algebroids, if and only if the ideal I satisfies:
-
(HI1)
 $\varepsilon (I) = 0$
;
$\varepsilon (I) = 0$
; -
(HI2)
 $\Delta (I) \subseteq \operatorname {Im}({\mathcal H}\otimes _{A}I + I\otimes _{A}{\mathcal H})$
;
$\Delta (I) \subseteq \operatorname {Im}({\mathcal H}\otimes _{A}I + I\otimes _{A}{\mathcal H})$
; -
(HI3)
 ${\mathcal S}(I) \subseteq I$
(and so
${\mathcal S}(I) \subseteq I$
(and so
 ${\mathcal S}(I) = I$
).
${\mathcal S}(I) = I$
).
An ideal
![]() $I \subseteq {\mathcal H}$
satisfying (HI1) and (HI2) will be called a wide bi-ideal of
$I \subseteq {\mathcal H}$
satisfying (HI1) and (HI2) will be called a wide bi-ideal of
![]() $(A,{\mathcal H})$
. When I satisfies (HI3) as well, it will be called a wide Hopf ideal of
$(A,{\mathcal H})$
. When I satisfies (HI3) as well, it will be called a wide Hopf ideal of
![]() $(A,{\mathcal H})$
.
$(A,{\mathcal H})$
.
Remark 4.8 The terminology “wide” introduced above is justified by the fact that if
![]() $I \subseteq {\mathcal H}$
is a wide Hopf ideal, then
$I \subseteq {\mathcal H}$
is a wide Hopf ideal, then
![]() $\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{{\mathcal H}/I}(\Bbbk )\big )$
is a wide subgroupoid of
$\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{{\mathcal H}/I}(\Bbbk )\big )$
is a wide subgroupoid of
![]() $\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{{\mathcal H}}(\Bbbk )\big )$
in the sense of [Reference Mackenzie26, Chapter I, Definition 2.4], that is to say, the two groupoids share the same set of objects. A more general notion of ideal for a Hopf algebroid would involve considering at the same time an ideal
$\big (\mathscr {G}_A(\Bbbk ),\mathscr {G}_{{\mathcal H}}(\Bbbk )\big )$
in the sense of [Reference Mackenzie26, Chapter I, Definition 2.4], that is to say, the two groupoids share the same set of objects. A more general notion of ideal for a Hopf algebroid would involve considering at the same time an ideal
![]() $I_A$
in A and an ideal
$I_A$
in A and an ideal
![]() $I_{\mathcal H}$
in
$I_{\mathcal H}$
in
![]() ${\mathcal H}$
such that the canonical projections
${\mathcal H}$
such that the canonical projections
![]() $(\pi _A\colon A \to A/I_A,\pi _{\mathcal H}\colon {\mathcal H} \to {\mathcal H}/I_{\mathcal H})$
form a morphism of Hopf algebroids, but we do not discuss this case herein. See Section 3.2 of [Reference Ghobadi19] for additional details.
$(\pi _A\colon A \to A/I_A,\pi _{\mathcal H}\colon {\mathcal H} \to {\mathcal H}/I_{\mathcal H})$
form a morphism of Hopf algebroids, but we do not discuss this case herein. See Section 3.2 of [Reference Ghobadi19] for additional details.
In what follows, we are mainly concerned with wide subgroupoids and wide ideals; hence, we will often omit the adjective “wide.” For the sake of completeness, the following proposition can be proved by finding inspiration from the proof of Proposition 3.3.
Proposition 4.9 Let
![]() ${\mathcal H}$
and
${\mathcal H}$
and
![]() ${\mathcal K}$
be bialgebroids (resp. Hopf algebroids) over the same base algebra A, and let
${\mathcal K}$
be bialgebroids (resp. Hopf algebroids) over the same base algebra A, and let
![]() $\phi : {\mathcal H} \to {\mathcal K}$
be a morphism of bialgebroids (resp. Hopf algebroids) over A. If the two-sided ideal
$\phi : {\mathcal H} \to {\mathcal K}$
be a morphism of bialgebroids (resp. Hopf algebroids) over A. If the two-sided ideal
![]() $I \subseteq {\mathcal H}$
is a bi-ideal (resp. Hopf ideal) of
$I \subseteq {\mathcal H}$
is a bi-ideal (resp. Hopf ideal) of
![]() ${\mathcal H}$
and if we denote by
${\mathcal H}$
and if we denote by
![]() $\pi :{\mathcal H} \to {\mathcal H}/I$
the canonical projection, then:
$\pi :{\mathcal H} \to {\mathcal H}/I$
the canonical projection, then:
-
•
 $(A,{\mathcal H}/I)$
has a unique bialgebroid (resp. Hopf algebroid) structure such that
$(A,{\mathcal H}/I)$
has a unique bialgebroid (resp. Hopf algebroid) structure such that
 $\pi $
becomes a morphism of bialgebroids (resp. Hopf algebroids) over A.
$\pi $
becomes a morphism of bialgebroids (resp. Hopf algebroids) over A. -
•
 $\ker (\phi )$
is a bi-ideal (resp. Hopf ideal) of
$\ker (\phi )$
is a bi-ideal (resp. Hopf ideal) of
 $(A,{\mathcal H})$
.
$(A,{\mathcal H})$
. -
• For any bi-ideal (resp. Hopf ideal)
 $I \subseteq \ker (\phi )$
, there exists a unique morphism of bialgebroids (resp. Hopf algebroids) over A,
$I \subseteq \ker (\phi )$
, there exists a unique morphism of bialgebroids (resp. Hopf algebroids) over A,
 $\tilde {\phi }:{\mathcal H}/I \to {\mathcal K}$
, such that
$\tilde {\phi }:{\mathcal H}/I \to {\mathcal K}$
, such that
 $\tilde {\phi } \circ \pi = \phi $
.
$\tilde {\phi } \circ \pi = \phi $
.
Now, let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid and consider the ideal
$(A,{\mathcal H})$
be a commutative Hopf algebroid and consider the ideal
![]() $\langle s-t \rangle $
generated by the vector subspace
$\langle s-t \rangle $
generated by the vector subspace
![]() $\{s(a) - t(a) \mid a \in A\}$
. Since
$\{s(a) - t(a) \mid a \in A\}$
. Since
![]() $s(a) - t(a) \in {\mathcal P}_{A}({\mathcal H})$
(the space of primitive elements) for every
$s(a) - t(a) \in {\mathcal P}_{A}({\mathcal H})$
(the space of primitive elements) for every
![]() $a \in A$
,
$a \in A$
,
![]() $\langle s-t \rangle $
is a Hopf ideal in
$\langle s-t \rangle $
is a Hopf ideal in
![]() ${\mathcal H}$
. Its associated quotient Hopf algebroid will be denoted by
${\mathcal H}$
. Its associated quotient Hopf algebroid will be denoted by
![]() . For
. For
![]() $(A, {{\mathcal H}}_{(i)})$
, the source equals the target. That is, it is a commutative Hopf A-algebra. Denote by
$(A, {{\mathcal H}}_{(i)})$
, the source equals the target. That is, it is a commutative Hopf A-algebra. Denote by
![]() $\eta \colon A \to {{\mathcal H}}_{(i)}$
the unit map (that is,
$\eta \colon A \to {{\mathcal H}}_{(i)}$
the unit map (that is,
![]() $\eta (a) = s(a) + \langle s-t\rangle = t(a) + \langle s-t\rangle $
for all
$\eta (a) = s(a) + \langle s-t\rangle = t(a) + \langle s-t\rangle $
for all
![]() $a \in A$
) and by
$a \in A$
) and by
![]() ${\varpi }_{(i)} \colon {\mathcal H} \to {{\mathcal H}}_{(i)}$
the canonical projection sending x to
${\varpi }_{(i)} \colon {\mathcal H} \to {{\mathcal H}}_{(i)}$
the canonical projection sending x to
![]() $\overline {x} = x + \langle s-t \rangle $
.
$\overline {x} = x + \langle s-t \rangle $
.
Lemma 4.10 Let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid. Then the presheaf of groupoids
$(A,{\mathcal H})$
be a commutative Hopf algebroid. Then the presheaf of groupoids
![]() $\big (\mathscr {G}_A, \mathscr {G}_{\mathcal H}^{(i)}\big )$
obtained by considering the isotropy groupoid of
$\big (\mathscr {G}_A, \mathscr {G}_{\mathcal H}^{(i)}\big )$
obtained by considering the isotropy groupoid of
![]() $\big (\mathscr {G}_A(R), \mathscr {G}_{\mathcal H}(R)\big )$
for every R in
$\big (\mathscr {G}_A(R), \mathscr {G}_{\mathcal H}(R)\big )$
for every R in
![]() $\mathrm {CAlg}_{\Bbbk }$
is represented by the Hopf A-algebra
$\mathrm {CAlg}_{\Bbbk }$
is represented by the Hopf A-algebra
![]() ${{\mathcal H}}_{(i)}$
. In other words, we have an isomorphism
${{\mathcal H}}_{(i)}$
. In other words, we have an isomorphism
natural in R, between the isotropy groupoid of
![]() $\big (\mathscr {G}_A, \mathscr {G}_{\mathcal H}\big )$
and the groupoid
$\big (\mathscr {G}_A, \mathscr {G}_{\mathcal H}\big )$
and the groupoid
![]() $\big (\mathscr {G}_A,\mathscr {G}_{{{\mathcal H}}_{(i)}}\big )$
.
$\big (\mathscr {G}_A,\mathscr {G}_{{{\mathcal H}}_{(i)}}\big )$
.
Proof Let R be a commutative
![]() $\Bbbk $
-algebra. The fact that the correspondence
$\Bbbk $
-algebra. The fact that the correspondence
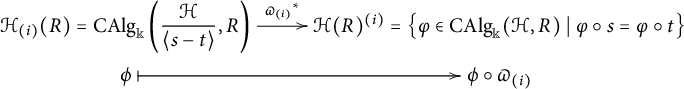
is bijective is almost tautological, and it is a morphism of groupoids because it is induced by a morphism of commutative Hopf algebroids. The naturality in R follows from the associativity of the composition.
Even for Hopf algebroids over noncommutative base algebras,
![]() ${\mathcal H}/\langle s-t \rangle $
forms a natural Hopf algebroid structure and is called the isotropy quotient of
${\mathcal H}/\langle s-t \rangle $
forms a natural Hopf algebroid structure and is called the isotropy quotient of
![]() ${\mathcal H}$
[Reference Ghobadi19]. In particular, Lemma 4.10 was previously discussed in Example 3.13 of [Reference Ghobadi19].
${\mathcal H}$
[Reference Ghobadi19]. In particular, Lemma 4.10 was previously discussed in Example 3.13 of [Reference Ghobadi19].
4.2.2 Comodule algebras and normal Hopf ideals
With an eye to the definition of normal Hopf ideals, we give the analog of the adjoint action for groupoids (see Section 4.1.2) in the Hopf algebroid context. To this aim, recall first that a (commutative) right
![]() ${\mathcal H}$
-comodule algebra for a commutative Hopf algebroid
${\mathcal H}$
-comodule algebra for a commutative Hopf algebroid
![]() $(A,{\mathcal H})$
is a (commutative) monoid in the symmetric monoidal category
$(A,{\mathcal H})$
is a (commutative) monoid in the symmetric monoidal category
![]() $ \textsf {Comod}{}^{{\mathcal H}}$
(see Remark 3.2). That is, a (commutative) right
$ \textsf {Comod}{}^{{\mathcal H}}$
(see Remark 3.2). That is, a (commutative) right
![]() $\mathcal{H}$
-comodule algebra is a (commutative) A-algebra a
$\mathcal{H}$
-comodule algebra is a (commutative) A-algebra a
![]() ${\mathcal R}$
(with structure map
${\mathcal R}$
(with structure map
![]() $r\colon A\to {\mathcal R}$
) which is also a right
$r\colon A\to {\mathcal R}$
) which is also a right
![]() ${\mathcal H}$
-comodule with coaction
${\mathcal H}$
-comodule with coaction
![]() $\delta _{{\mathcal R}}\colon {\mathcal R} \to {\mathcal R}\otimes _{A}{\mathcal H}, x \mapsto \sum x_{0} \otimes _{A} x_1$
, satisfying for all
$\delta _{{\mathcal R}}\colon {\mathcal R} \to {\mathcal R}\otimes _{A}{\mathcal H}, x \mapsto \sum x_{0} \otimes _{A} x_1$
, satisfying for all
![]() $x, y \in {\mathcal R}$
,
$x, y \in {\mathcal R}$
,
In others words, the coaction
![]() $\delta _{{\mathcal R}}$
is an A-algebra map, where
$\delta _{{\mathcal R}}$
is an A-algebra map, where
![]() ${\mathcal R}\otimes _{A}{\mathcal H}$
is seen as an A-algebra via
${\mathcal R}\otimes _{A}{\mathcal H}$
is seen as an A-algebra via
![]() $A \to {\mathcal R} \otimes _{A} {\mathcal H},a \mapsto 1_{{\mathcal R}}\otimes _{A} t(a)$
. A morphism of right
$A \to {\mathcal R} \otimes _{A} {\mathcal H},a \mapsto 1_{{\mathcal R}}\otimes _{A} t(a)$
. A morphism of right
![]() ${\mathcal H}$
-comodule algebras is an A-algebra map which is also a right
${\mathcal H}$
-comodule algebras is an A-algebra map which is also a right
![]() ${\mathcal H}$
-comodule morphism. Left
${\mathcal H}$
-comodule morphism. Left
![]() ${\mathcal H}$
-comodule algebras are analogously defined. Henceforth, all comodule algebras will be commutative comodule algebras. A trivial example of a comodule algebra is the base algebra A of a Hopf algebroid
${\mathcal H}$
-comodule algebras are analogously defined. Henceforth, all comodule algebras will be commutative comodule algebras. A trivial example of a comodule algebra is the base algebra A of a Hopf algebroid
![]() $(A, {\mathcal H})$
itself.
$(A, {\mathcal H})$
itself.
Proposition 4.11 Let
![]() $\mathscr {G}_{(A,{\mathcal H})} = (\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
be an affine groupoid scheme, and let
$\mathscr {G}_{(A,{\mathcal H})} = (\mathscr {G}_A,\mathscr {G}_{\mathcal H})$
be an affine groupoid scheme, and let
![]() $\mathscr {N}_{\mathcal B} = \mathrm {CAlg}_{\Bbbk }({\mathcal B},-)$
be an affine scheme, for
$\mathscr {N}_{\mathcal B} = \mathrm {CAlg}_{\Bbbk }({\mathcal B},-)$
be an affine scheme, for
![]() ${\mathcal B}$
in
${\mathcal B}$
in
![]() $\mathrm {CAlg}_{\Bbbk }$
. Then
$\mathrm {CAlg}_{\Bbbk }$
. Then
![]() $\mathscr {N}_{\mathcal B}(R)$
is a left
$\mathscr {N}_{\mathcal B}(R)$
is a left
![]() $\mathscr {G}_{(A,{\mathcal H})}(R)$
-set (naturally in R in
$\mathscr {G}_{(A,{\mathcal H})}(R)$
-set (naturally in R in
![]() $\mathrm {CAlg}_{\Bbbk }$
) if and only if
$\mathrm {CAlg}_{\Bbbk }$
) if and only if
![]() ${\mathcal B}$
is a right
${\mathcal B}$
is a right
![]() ${\mathcal H}$
-comodule algebra.
${\mathcal H}$
-comodule algebra.
Proof If
![]() $({\mathcal B},b:A\rightarrow {\mathcal B})$
is an A-algebra with a right
$({\mathcal B},b:A\rightarrow {\mathcal B})$
is an A-algebra with a right
![]() ${\mathcal H}$
-comodule algebra structure given by a coaction
${\mathcal H}$
-comodule algebra structure given by a coaction
![]() $\delta _{{\mathcal B}}$
, then
$\delta _{{\mathcal B}}$
, then
and
turn
![]() $\mathscr {N}_{\mathcal B}(R)$
into a left
$\mathscr {N}_{\mathcal B}(R)$
into a left
![]() $\mathscr {G}_{(A,{\mathcal H})}(R)$
-set. Conversely, if
$\mathscr {G}_{(A,{\mathcal H})}(R)$
-set. Conversely, if
![]() $\Big (\mathscr {N}_{\mathcal B}(R),\rho _R,\mu _R\Big )$
is a left
$\Big (\mathscr {N}_{\mathcal B}(R),\rho _R,\mu _R\Big )$
is a left
![]() $\mathscr {G}_{(A,{\mathcal H})}(R)$
-set natural in
$\mathscr {G}_{(A,{\mathcal H})}(R)$
-set natural in
![]() $\mathrm {CAlg}_{\Bbbk }$
, then
$\mathrm {CAlg}_{\Bbbk }$
, then
and
make of
![]() ${\mathcal B}$
a right
${\mathcal B}$
a right
![]() ${\mathcal H}$
-comodule algebra.
${\mathcal H}$
-comodule algebra.
In the setting of Proposition 4.11, we say that
![]() $\mathscr {N}_{\mathcal B}$
is an affine (left)
$\mathscr {N}_{\mathcal B}$
is an affine (left)
![]() $\mathscr {G}_{(A,{\mathcal H})}$
-set.
$\mathscr {G}_{(A,{\mathcal H})}$
-set.
Note that, for a right
![]() ${\mathcal H}$
-comodule algebra
${\mathcal H}$
-comodule algebra
![]() $({\mathcal R},r)$
, the
$({\mathcal R},r)$
, the
![]() $\Bbbk $
-vector subspace
$\Bbbk $
-vector subspace
of
![]() ${\mathcal H}$
-coinvariant elements is a
${\mathcal H}$
-coinvariant elements is a
![]() $\Bbbk $
-subalgebra of
$\Bbbk $
-subalgebra of
![]() ${\mathcal R}$
(this follows easily from (4.4)).
${\mathcal R}$
(this follows easily from (4.4)).
Remark 4.12 In general,
![]() ${{\mathcal R}}^{\textsf {co}{{\mathcal H}}}$
does not necessarily contain the image
${{\mathcal R}}^{\textsf {co}{{\mathcal H}}}$
does not necessarily contain the image
![]() $r(A)$
of A, unless one makes additional assumptions. For instance, if the source and target of
$r(A)$
of A, unless one makes additional assumptions. For instance, if the source and target of
![]() ${\mathcal H}$
are equal, then it does.
${\mathcal H}$
are equal, then it does.
Dually to the construction of the left translation groupoid, if
![]() $({\mathcal R},r)$
is a right
$({\mathcal R},r)$
is a right
![]() ${\mathcal H}$
-comodule algebra, then
${\mathcal H}$
-comodule algebra, then
![]() $({\mathcal R}, {\mathcal R}\otimes _{A}{\mathcal H})$
admits a natural structure of commutative Hopf algebroid such that
$({\mathcal R}, {\mathcal R}\otimes _{A}{\mathcal H})$
admits a natural structure of commutative Hopf algebroid such that
![]() $(r, 1_{{{\mathcal R}}}\otimes _{A}-)\colon (A,{\mathcal H}) \to ({\mathcal R},{\mathcal R}\otimes _{A}{\mathcal H})$
is a morphism of Hopf algebroids. Namely,
$(r, 1_{{{\mathcal R}}}\otimes _{A}-)\colon (A,{\mathcal H}) \to ({\mathcal R},{\mathcal R}\otimes _{A}{\mathcal H})$
is a morphism of Hopf algebroids. Namely,
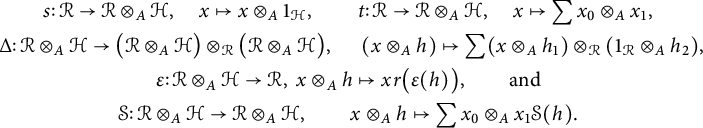 $$ \begin{gather*} s\colon {\mathcal R} \to {\mathcal R} \otimes_{A} {\mathcal H}, \quad x \mapsto x \otimes_{A} 1_{\mathcal H}, \qquad t\colon {\mathcal R} \to {\mathcal R} \otimes_{A} {\mathcal H}, \quad x \mapsto \sum x_0 \otimes_{A} x_1, \\ \Delta\colon {\mathcal R} \otimes_{A} {\mathcal H} \to \big({\mathcal R} \otimes_{A} {\mathcal H}\big) \otimes_{{\mathcal R}} \big({\mathcal R} \otimes_{A} {\mathcal H}\big), \kern-7pt\qquad (x \otimes_{A} h) \mapsto \sum (x \otimes_{A} h_1) \otimes_{{\mathcal R}} (1_{\mathcal R} \otimes_{A} h_2), \\ \varepsilon\colon {\mathcal R} \otimes_{A} {\mathcal H} \to {\mathcal R}, \ x \otimes_{A} h \mapsto x r\big(\varepsilon(h)\big), \qquad \text{and} \\ {\mathcal S} \colon {\mathcal R} \otimes_{A} {\mathcal H} \to {\mathcal R} \otimes_{A} {\mathcal H}, \qquad x \otimes_{A} h \mapsto \sum x_0 \otimes_{A} x_1{\mathcal S}(h). \end{gather*} $$
$$ \begin{gather*} s\colon {\mathcal R} \to {\mathcal R} \otimes_{A} {\mathcal H}, \quad x \mapsto x \otimes_{A} 1_{\mathcal H}, \qquad t\colon {\mathcal R} \to {\mathcal R} \otimes_{A} {\mathcal H}, \quad x \mapsto \sum x_0 \otimes_{A} x_1, \\ \Delta\colon {\mathcal R} \otimes_{A} {\mathcal H} \to \big({\mathcal R} \otimes_{A} {\mathcal H}\big) \otimes_{{\mathcal R}} \big({\mathcal R} \otimes_{A} {\mathcal H}\big), \kern-7pt\qquad (x \otimes_{A} h) \mapsto \sum (x \otimes_{A} h_1) \otimes_{{\mathcal R}} (1_{\mathcal R} \otimes_{A} h_2), \\ \varepsilon\colon {\mathcal R} \otimes_{A} {\mathcal H} \to {\mathcal R}, \ x \otimes_{A} h \mapsto x r\big(\varepsilon(h)\big), \qquad \text{and} \\ {\mathcal S} \colon {\mathcal R} \otimes_{A} {\mathcal H} \to {\mathcal R} \otimes_{A} {\mathcal H}, \qquad x \otimes_{A} h \mapsto \sum x_0 \otimes_{A} x_1{\mathcal S}(h). \end{gather*} $$
This is called the left translation Hopf algebroid of
![]() $(A, {\mathcal H})$
along r. Of course, if
$(A, {\mathcal H})$
along r. Of course, if
![]() ${}_{s} {{{\mathcal H}}}$
is flat over A, then
${}_{s} {{{\mathcal H}}}$
is flat over A, then
![]() ${\mathcal R}\otimes _{A}{\mathcal H}$
is flat over
${\mathcal R}\otimes _{A}{\mathcal H}$
is flat over
![]() ${\mathcal R}$
(see [Reference El Kaoutit and Kowalzig15, Lemma 3.4] for more properties).
${\mathcal R}$
(see [Reference El Kaoutit and Kowalzig15, Lemma 3.4] for more properties).
Now, dually to the case of groupoids, we introduce the adjoint coaction.
Proposition 4.13 The pair
![]() $({{\mathcal H}}_{(i)}, \eta )$
is a right
$({{\mathcal H}}_{(i)}, \eta )$
is a right
![]() ${\mathcal H}$
-comodule algebra with coaction defined by
${\mathcal H}$
-comodule algebra with coaction defined by
In particular,
![]() $({{\mathcal H}}_{(i)}, {{\mathcal H}}_{(i)}\otimes _{A}{\mathcal H})$
is a commutative Hopf algebroid (it is the left translation Hopf algebroid along
$({{\mathcal H}}_{(i)}, {{\mathcal H}}_{(i)}\otimes _{A}{\mathcal H})$
is a commutative Hopf algebroid (it is the left translation Hopf algebroid along
![]() $\eta $
).
$\eta $
).
Proof The fact that
![]() $\delta _{{{\mathcal H}}_{(i)}}$
is well defined can be deduced by using the following map:
$\delta _{{{\mathcal H}}_{(i)}}$
is well defined can be deduced by using the following map:
which is well defined and right A-linear. The map
![]() $\delta _{{{\mathcal H}}_{(i)}}$
is clearly right A-linear, that is,
$\delta _{{{\mathcal H}}_{(i)}}$
is clearly right A-linear, that is,
![]() $\delta _{{{\mathcal H}}_{(i)}}\Big ( \overline {h}\eta (a)\Big ) = \delta _{{{\mathcal H}}_{(i)}}(\overline {h})t(a)$
for every
$\delta _{{{\mathcal H}}_{(i)}}\Big ( \overline {h}\eta (a)\Big ) = \delta _{{{\mathcal H}}_{(i)}}(\overline {h})t(a)$
for every
![]() $a \in A$
and
$a \in A$
and
![]() $\overline {h} \in {{\mathcal H}}_{(i)}$
. Aside from the coaction being well defined, the rest of the proof showing the coassociativity and counital property of
$\overline {h} \in {{\mathcal H}}_{(i)}$
. Aside from the coaction being well defined, the rest of the proof showing the coassociativity and counital property of
![]() $\delta $
and the comodule algebra structure on
$\delta $
and the comodule algebra structure on
![]() ${{\mathcal H}}_{(i)}$
follow exactly as in the case of the right adjoint coaction on ordinary Hopf algebras, by simply using Sweedler’s notation. Therefore,
${{\mathcal H}}_{(i)}$
follow exactly as in the case of the right adjoint coaction on ordinary Hopf algebras, by simply using Sweedler’s notation. Therefore,
![]() $({{\mathcal H}}_{(i)}, \delta _{{{\mathcal H}}_{(i)}})$
is a right
$({{\mathcal H}}_{(i)}, \delta _{{{\mathcal H}}_{(i)}})$
is a right
![]() ${\mathcal H}$
-comodule. Since
${\mathcal H}$
-comodule. Since
![]() $\delta _{{{\mathcal H}}_{(i)}}$
is manifestly multiplicative and unital,
$\delta _{{{\mathcal H}}_{(i)}}$
is manifestly multiplicative and unital,
![]() $({{\mathcal H}}_{(i)}, \eta )$
is a right
$({{\mathcal H}}_{(i)}, \eta )$
is a right
![]() ${\mathcal H}$
-comodule algebra.
${\mathcal H}$
-comodule algebra.
Let I be an ideal of
![]() ${\mathcal H}$
which contains
${\mathcal H}$
which contains
![]() $\langle s-t \rangle $
. We denote by
$\langle s-t \rangle $
. We denote by
![]() ${I}_{(i)}$
its image in
${I}_{(i)}$
its image in
![]() ${{\mathcal H}}_{(i)}$
:
${{\mathcal H}}_{(i)}$
:
![]() .
.
Definition 4.2 Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid. A Hopf ideal I of
$(A, {\mathcal H})$
be a commutative Hopf algebroid. A Hopf ideal I of
![]() ${\mathcal H}$
is said to be normal if it satisfies the following conditions:
${\mathcal H}$
is said to be normal if it satisfies the following conditions:
-
(NI1)
 $\langle s-t \rangle \subseteq I$
.
$\langle s-t \rangle \subseteq I$
. -
(NI2) For every
 $\overline {x} \in {I}_{(i)}$
, we have
$\overline {x} \in {I}_{(i)}$
, we have
 $\delta _{{{\mathcal H}}_{(i)}}\big (\overline {x}\big ) = \sum \overline {x_2} \otimes _{A} {\mathcal S}(x_1)x_3 \in \operatorname {Im}\left ({I}_{(i)} \otimes _{A} {\mathcal H}\right )$
.
$\delta _{{{\mathcal H}}_{(i)}}\big (\overline {x}\big ) = \sum \overline {x_2} \otimes _{A} {\mathcal S}(x_1)x_3 \in \operatorname {Im}\left ({I}_{(i)} \otimes _{A} {\mathcal H}\right )$
.
Remark 4.14 If
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat, then (NI2) is equivalent to requiring that the image of
${}_{s} {{{\mathcal H}}}$
is A-flat, then (NI2) is equivalent to requiring that the image of
![]() ${I}_{(i)}$
is a right
${I}_{(i)}$
is a right
![]() ${\mathcal H}$
-subcomodule of
${\mathcal H}$
-subcomodule of
![]() ${{\mathcal H}}_{(i)}$
with respect to the coaction (4.5). Namely, that there exists
${{\mathcal H}}_{(i)}$
with respect to the coaction (4.5). Namely, that there exists
![]() $\delta _{{I}_{(i)}}\colon {I}_{(i)} \to {I}_{(i)} \otimes _{A} {\mathcal H}$
such that the following diagram commutes:
$\delta _{{I}_{(i)}}\colon {I}_{(i)} \to {I}_{(i)} \otimes _{A} {\mathcal H}$
such that the following diagram commutes:
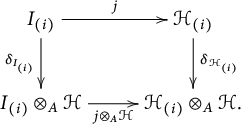
▲
For commutative Hopf algebroids with source equal to target, that is, for Hopf algebras over a commutative algebra, one recovers the classical definition. Notice further that in this latter case, the associated isotropy Hopf algebra coincides with the Hopf algebroid itself.
Lemma 4.15 Let I be a normal Hopf ideal in
![]() $(A,{\mathcal H})$
. Then
$(A,{\mathcal H})$
. Then
![]() ${I}_{(i)}$
is a normal Hopf ideal in
${I}_{(i)}$
is a normal Hopf ideal in
![]() $(A, {{\mathcal H}}_{(i)})$
.
$(A, {{\mathcal H}}_{(i)})$
.
Proof Straightforward.
The following proposition is the Hopf algebroid analog of Lemma 4.3.
Proposition 4.16 Let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid, and let
$(A,{\mathcal H})$
be a commutative Hopf algebroid, and let
![]() $I \subseteq {\mathcal H}$
be a Hopf ideal. Then I is normal if and only if
$I \subseteq {\mathcal H}$
be a Hopf ideal. Then I is normal if and only if
![]() $\langle s-t \rangle \subseteq I$
and
$\langle s-t \rangle \subseteq I$
and
![]() ${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
is a quotient
${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
is a quotient
![]() ${\mathcal H}$
-comodule of
${\mathcal H}$
-comodule of
![]() ${{\mathcal H}}_{(i)}$
with respect to the coaction (4.5).
${{\mathcal H}}_{(i)}$
with respect to the coaction (4.5).
Proof The statement follows from the fact that I is normal if and only if the left-hand side square in the following diagram with exact rows commutes:
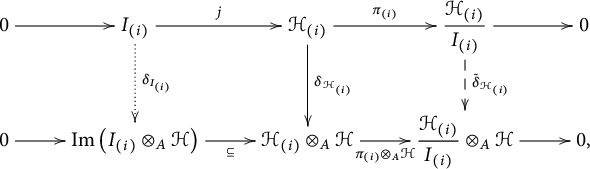
if and only if the right-hand side square commutes, because
![]() $\operatorname {Im}\left ({I}_{(i)} \otimes _{A} {\mathcal H}\right ) = \ker \left ({\pi }_{(i)} \otimes _{A} {\mathcal H}\right )$
.
$\operatorname {Im}\left ({I}_{(i)} \otimes _{A} {\mathcal H}\right ) = \ker \left ({\pi }_{(i)} \otimes _{A} {\mathcal H}\right )$
.
Let
![]() $\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
be an affine subgroupoid of
$\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
be an affine subgroupoid of
![]() $\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
(i.e.,
$\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
(i.e.,
![]() $I \subseteq {\mathcal H}$
is a Hopf ideal). We say that
$I \subseteq {\mathcal H}$
is a Hopf ideal). We say that
![]() $\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
is a normal affine subgroupoid of
$\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
is a normal affine subgroupoid of
![]() $\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
if and only if
$\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
if and only if
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}/I}(R)\big )$
is a normal subgroupoid of
$\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}/I}(R)\big )$
is a normal subgroupoid of
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
in the sense of Section 4.1.2, for all R in
$\big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
in the sense of Section 4.1.2, for all R in
![]() $\mathrm {CAlg}_{\Bbbk }$
. The following proposition shows that normal Hopf ideals are in bijective correspondence with normal affine subgroupoids.
$\mathrm {CAlg}_{\Bbbk }$
. The following proposition shows that normal Hopf ideals are in bijective correspondence with normal affine subgroupoids.
Proposition 4.17 Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid. There is a one-to-one correspondence between normal Hopf ideals of
$(A, {\mathcal H})$
be a commutative Hopf algebroid. There is a one-to-one correspondence between normal Hopf ideals of
![]() $(A,{\mathcal H})$
and normal affine subgroupoids of
$(A,{\mathcal H})$
and normal affine subgroupoids of
![]() $\big (\mathscr {G}_A, \mathscr {G}_{\mathcal H}\big )$
.
$\big (\mathscr {G}_A, \mathscr {G}_{\mathcal H}\big )$
.
Proof Let I be a normal Hopf ideal of
![]() ${\mathcal H}$
. Then, in view of (NI1) and Lemma 4.15,
${\mathcal H}$
. Then, in view of (NI1) and Lemma 4.15,
![]() ${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
is a commutative Hopf A-algebra with a surjective morphism of commutative Hopf algebroids
${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
is a commutative Hopf A-algebra with a surjective morphism of commutative Hopf algebroids
![]() $(\operatorname {Id}_A,\tilde {\pi }) \colon (A,{\mathcal H}) \to (A, {{\mathcal H}}_{(i)}/{I}_{(i)})$
, where
$(\operatorname {Id}_A,\tilde {\pi }) \colon (A,{\mathcal H}) \to (A, {{\mathcal H}}_{(i)}/{I}_{(i)})$
, where
![]() $\tilde {\pi }\colon {\mathcal H} \to {{\mathcal H}}_{(i)}/{I}_{(i)}$
is induced by
$\tilde {\pi }\colon {\mathcal H} \to {{\mathcal H}}_{(i)}/{I}_{(i)}$
is induced by
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
, up to the isomorphism above. We have then the affine subgroupoid
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
, up to the isomorphism above. We have then the affine subgroupoid
![]() $\Big (\mathscr {G}_A,\mathscr {G}_{{{\mathcal H}}_{(i)}/{I}_{(i)}}\Big )$
of
$\Big (\mathscr {G}_A,\mathscr {G}_{{{\mathcal H}}_{(i)}/{I}_{(i)}}\Big )$
of
![]() $\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
. For R in
$\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
. For R in
![]() $\mathrm {CAlg}_{\Bbbk }$
, consider
$\mathrm {CAlg}_{\Bbbk }$
, consider
![]() $(\operatorname {Id},\tilde {\pi }^*) \colon \Big (\mathscr {G}_A(R),\mathscr {G}_{{{\mathcal H}}_{(i)}/{I}_{(i)}}(R)\Big ) \hookrightarrow \big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
. Condition (NG0) is always satisfied in our treatment. Condition (NG1) is satisfied because for every
$(\operatorname {Id},\tilde {\pi }^*) \colon \Big (\mathscr {G}_A(R),\mathscr {G}_{{{\mathcal H}}_{(i)}/{I}_{(i)}}(R)\Big ) \hookrightarrow \big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
. Condition (NG0) is always satisfied in our treatment. Condition (NG1) is satisfied because for every
![]() $\varphi \in \mathrm {CAlg}_{\Bbbk }\big ({{\mathcal H}}_{(i)}/{I}_{(i)},R\big )$
, we have
$\varphi \in \mathrm {CAlg}_{\Bbbk }\big ({{\mathcal H}}_{(i)}/{I}_{(i)},R\big )$
, we have
Concerning condition (NG2), for every
![]() $\psi \in \mathrm {CAlg}_{\Bbbk }({\mathcal H},R)$
and for every
$\psi \in \mathrm {CAlg}_{\Bbbk }({\mathcal H},R)$
and for every
![]() $\varphi \in \mathrm {CAlg}_{\Bbbk }\big ({{\mathcal H}}_{(i)}/{I}_{(i)},R\big )$
such that
$\varphi \in \mathrm {CAlg}_{\Bbbk }\big ({{\mathcal H}}_{(i)}/{I}_{(i)},R\big )$
such that
![]() $\varphi \circ (\tilde {\pi }\circ s) = \psi \circ s = \varphi \circ (\tilde {\pi } \circ t)$
(i.e., source and target of
$\varphi \circ (\tilde {\pi }\circ s) = \psi \circ s = \varphi \circ (\tilde {\pi } \circ t)$
(i.e., source and target of
![]() $\varphi $
coincide with the source of
$\varphi $
coincide with the source of
![]() $\psi $
), set
$\psi $
), set
![]() . Notice that
. Notice that
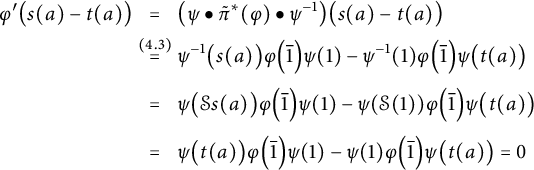 $$ \begin{align*} \varphi'\big(s(a)-t(a)\big) & \stackrel{\phantom{(4.3)}}{=} \big(\psi \bullet \tilde{\pi}^*(\varphi) \bullet \psi^{-1}\big)\big(s(a)-t(a)\big) \\ & \stackrel{(4.3)}{=} \psi^{-1}\big(s(a)\big)\varphi\Big(\overline{1}\Big)\psi(1) - \psi^{-1}(1)\varphi\Big(\overline{1}\Big)\psi\big(t(a)\big) \\ & \stackrel{\phantom{(4.3)}}{=}\psi\big({\mathcal S} s(a)\big)\varphi\Big(\overline{1}\Big)\psi(1) - \psi({\mathcal S} (1))\varphi\Big(\overline{1}\Big)\psi\big(t(a)\big) \\ & \stackrel{\phantom{(4.3)}}{=}\psi\big(t(a)\big)\varphi\Big(\overline{1}\Big)\psi(1) - \psi(1)\varphi\Big(\overline{1}\Big)\psi\big(t(a)\big) = 0 \end{align*} $$
$$ \begin{align*} \varphi'\big(s(a)-t(a)\big) & \stackrel{\phantom{(4.3)}}{=} \big(\psi \bullet \tilde{\pi}^*(\varphi) \bullet \psi^{-1}\big)\big(s(a)-t(a)\big) \\ & \stackrel{(4.3)}{=} \psi^{-1}\big(s(a)\big)\varphi\Big(\overline{1}\Big)\psi(1) - \psi^{-1}(1)\varphi\Big(\overline{1}\Big)\psi\big(t(a)\big) \\ & \stackrel{\phantom{(4.3)}}{=}\psi\big({\mathcal S} s(a)\big)\varphi\Big(\overline{1}\Big)\psi(1) - \psi({\mathcal S} (1))\varphi\Big(\overline{1}\Big)\psi\big(t(a)\big) \\ & \stackrel{\phantom{(4.3)}}{=}\psi\big(t(a)\big)\varphi\Big(\overline{1}\Big)\psi(1) - \psi(1)\varphi\Big(\overline{1}\Big)\psi\big(t(a)\big) = 0 \end{align*} $$
for all
![]() $a \in A$
, whence there exists a unique
$a \in A$
, whence there exists a unique
![]() $\tilde {\varphi }'\colon {{\mathcal H}}_{(i)} \to R$
such that
$\tilde {\varphi }'\colon {{\mathcal H}}_{(i)} \to R$
such that
![]() $\tilde {\varphi }' \circ {\varpi }_{(i)} = \varphi '$
. Now, for every
$\tilde {\varphi }' \circ {\varpi }_{(i)} = \varphi '$
. Now, for every
![]() $\overline {x} = {\varpi }_{(i)}(x) \in {I}_{(i)}$
, we have that
$\overline {x} = {\varpi }_{(i)}(x) \in {I}_{(i)}$
, we have that
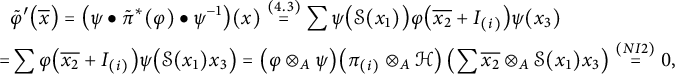 $$ \begin{align*} &\tilde{\varphi}'\big(\overline{x}\big) = \big(\psi \bullet \tilde{\pi}^*(\varphi) \bullet \psi^{-1}\big)(x) \stackrel{(4.3)}{=} \sum\psi\big({\mathcal S}(x_1)\big)\varphi\big(\overline{x_2} + {I}_{(i)}\big)\psi(x_3) \\ = &\sum\varphi\big(\overline{x_2} + {I}_{(i)}\big)\psi\big({\mathcal S}(x_1)x_3\big) = \big(\varphi \otimes_{A} \psi\big)\big({\pi}_{(i)} \otimes_{A} {\mathcal H}\big)\left(\sum\overline{x_2} \otimes_{A} {\mathcal S}(x_1)x_3\right) \stackrel{(NI2)}{=} 0, \end{align*} $$
$$ \begin{align*} &\tilde{\varphi}'\big(\overline{x}\big) = \big(\psi \bullet \tilde{\pi}^*(\varphi) \bullet \psi^{-1}\big)(x) \stackrel{(4.3)}{=} \sum\psi\big({\mathcal S}(x_1)\big)\varphi\big(\overline{x_2} + {I}_{(i)}\big)\psi(x_3) \\ = &\sum\varphi\big(\overline{x_2} + {I}_{(i)}\big)\psi\big({\mathcal S}(x_1)x_3\big) = \big(\varphi \otimes_{A} \psi\big)\big({\pi}_{(i)} \otimes_{A} {\mathcal H}\big)\left(\sum\overline{x_2} \otimes_{A} {\mathcal S}(x_1)x_3\right) \stackrel{(NI2)}{=} 0, \end{align*} $$
whence there exists a unique
![]() $\phi \colon {{\mathcal H}}_{(i)}/{I}_{(i)} \to R$
such that
$\phi \colon {{\mathcal H}}_{(i)}/{I}_{(i)} \to R$
such that
![]() $\phi \circ {\pi }_{(i)} = \tilde {\varphi }'$
. Summing up,
$\phi \circ {\pi }_{(i)} = \tilde {\varphi }'$
. Summing up,
![]() $\psi \bullet \tilde {\pi }^*(\varphi ) \bullet \psi ^{-1} = \tilde {\pi }^*(\phi )$
for some
$\psi \bullet \tilde {\pi }^*(\varphi ) \bullet \psi ^{-1} = \tilde {\pi }^*(\phi )$
for some
![]() $\phi \in \mathscr {G}_{{{\mathcal H}}_{(i)}/{I}_{(i)}}(R)$
and so (NG2) is satisfied.
$\phi \in \mathscr {G}_{{{\mathcal H}}_{(i)}/{I}_{(i)}}(R)$
and so (NG2) is satisfied.
Conversely, take a normal affine subgroupoid
![]() $\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
of
$\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
of
![]() $\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
induced by
$\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
induced by
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
. By definition, I is a Hopf ideal of
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
. By definition, I is a Hopf ideal of
![]() ${\mathcal H}$
. Moreover, for any commutative
${\mathcal H}$
. Moreover, for any commutative
![]() $\Bbbk $
-algebra R and for any
$\Bbbk $
-algebra R and for any
![]() $\varphi \in \mathrm {CAlg}_{\Bbbk }\big ({\mathcal H}/I,R\big )$
, we have that
$\varphi \in \mathrm {CAlg}_{\Bbbk }\big ({\mathcal H}/I,R\big )$
, we have that
![]() $\varphi \circ (\pi \circ s) = \varphi \circ (\pi \circ t)$
, because in
$\varphi \circ (\pi \circ s) = \varphi \circ (\pi \circ t)$
, because in
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}/I}(R)\big )$
the only arrows that we have are loops. By taking
$\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}/I}(R)\big )$
the only arrows that we have are loops. By taking
![]() $R={\mathcal H}/I$
and
$R={\mathcal H}/I$
and
![]() $\varphi = \operatorname {Id}_{{\mathcal H}/I}$
, we get
$\varphi = \operatorname {Id}_{{\mathcal H}/I}$
, we get
![]() $\pi \circ t = \pi \circ s $
, which shows that
$\pi \circ t = \pi \circ s $
, which shows that
![]() $\langle s - t \rangle \subseteq I$
and hence (NI1) is satisfied and
$\langle s - t \rangle \subseteq I$
and hence (NI1) is satisfied and
![]() ${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
. We still need to check condition (NI2). For this, recall from Lemma 4.3 that
${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
. We still need to check condition (NI2). For this, recall from Lemma 4.3 that
![]() $\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
is a normal affine subgroupoid of
$\big (\mathscr {G}_A,\mathscr {G}_{{\mathcal H}/I}\big )$
is a normal affine subgroupoid of
![]() $\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
if and only if
$\big (\mathscr {G}_A,\mathscr {G}_{\mathcal H}\big )$
if and only if
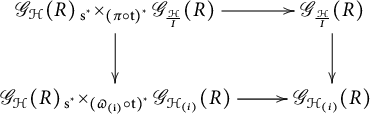
commutes for every R in
![]() $\mathrm {CAlg}_{\Bbbk }$
, if and only if there exists a right
$\mathrm {CAlg}_{\Bbbk }$
, if and only if there exists a right
![]() ${\mathcal H}$
-comodule algebra structure
${\mathcal H}$
-comodule algebra structure
![]() $\delta _{{\mathcal H}/I}$
on
$\delta _{{\mathcal H}/I}$
on
![]() ${\mathcal H}/I$
such that
${\mathcal H}/I$
such that
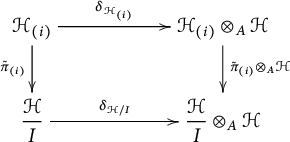
commutes (where
![]() ${\tilde {\pi }}_{(i)}$
is the composition
${\tilde {\pi }}_{(i)}$
is the composition
![]() ${{\mathcal H}}_{(i)} \xrightarrow {{\pi }_{(i)}} {{\mathcal H}}_{(i)}/{I}_{(i)} \cong {\mathcal H}/I$
with kernel
${{\mathcal H}}_{(i)} \xrightarrow {{\pi }_{(i)}} {{\mathcal H}}_{(i)}/{I}_{(i)} \cong {\mathcal H}/I$
with kernel
![]() ${I}_{(i)}$
), if and only if
${I}_{(i)}$
), if and only if
![]() $\delta _{{{\mathcal H}}_{(i)}}\big ({I}_{(i)}\big ) \subseteq \ker \big ({\tilde {\pi }}_{(i)} \otimes _{A} {\mathcal H}\big ) = \operatorname {Im}\big ({I}_{(i)} \otimes _{A} {\mathcal H}\big )$
.
$\delta _{{{\mathcal H}}_{(i)}}\big ({I}_{(i)}\big ) \subseteq \ker \big ({\tilde {\pi }}_{(i)} \otimes _{A} {\mathcal H}\big ) = \operatorname {Im}\big ({I}_{(i)} \otimes _{A} {\mathcal H}\big )$
.
Remark 4.18 The quotient
![]() ${{\mathcal H}}_{(i)}$
admits also a left
${{\mathcal H}}_{(i)}$
admits also a left
![]() ${\mathcal H}$
-comodule structure, which is related to the right comodule structure above via the isomorphism between the category of left
${\mathcal H}$
-comodule structure, which is related to the right comodule structure above via the isomorphism between the category of left
![]() ${\mathcal H}$
-comodules and the category of right
${\mathcal H}$
-comodules and the category of right
![]() ${\mathcal H}$
-comodules provided by the antipode: if
${\mathcal H}$
-comodules provided by the antipode: if
![]() $\left (N,\delta \colon n \mapsto \sum n_0 \otimes _{A} n_1 \right )$
is a right
$\left (N,\delta \colon n \mapsto \sum n_0 \otimes _{A} n_1 \right )$
is a right
![]() ${\mathcal H}$
-comodule, then N with
${\mathcal H}$
-comodule, then N with
![]() $\partial \colon N \to {\mathcal H} \otimes _{A} N, n \mapsto \sum {\mathcal S}(n_{1}) \otimes _{A} n_0$
, is a left
$\partial \colon N \to {\mathcal H} \otimes _{A} N, n \mapsto \sum {\mathcal S}(n_{1}) \otimes _{A} n_0$
, is a left
![]() ${\mathcal H}$
-comodule (recall that right
${\mathcal H}$
-comodule (recall that right
![]() ${\mathcal H}$
-comodules are, in fact, symmetric A-bimodules with the right–left being defined from (3.4)). The left
${\mathcal H}$
-comodules are, in fact, symmetric A-bimodules with the right–left being defined from (3.4)). The left
![]() ${\mathcal H}$
-coaction on
${\mathcal H}$
-coaction on
![]() ${{\mathcal H}}_{(i)}$
is then given by
${{\mathcal H}}_{(i)}$
is then given by
![]() $\partial _{{{\mathcal H}}_{(i)}} \colon {{\mathcal H}}_{(i)} \to {\mathcal H} \otimes _{A} {{\mathcal H}}_{(i)}$
sending
$\partial _{{{\mathcal H}}_{(i)}} \colon {{\mathcal H}}_{(i)} \to {\mathcal H} \otimes _{A} {{\mathcal H}}_{(i)}$
sending
![]() $\overline {x}$
to
$\overline {x}$
to
![]() $\sum x_1{\mathcal S}(x_3) \otimes _{A} \overline {x_2}$
. This corresponds to the right action by conjugation given at the groupoid level by
$\sum x_1{\mathcal S}(x_3) \otimes _{A} \overline {x_2}$
. This corresponds to the right action by conjugation given at the groupoid level by
![]() $(f,g) \mapsto g^{-1} \bullet f \bullet g$
. If
$(f,g) \mapsto g^{-1} \bullet f \bullet g$
. If
![]() ${}_{s} {{{\mathcal H}}}$
is flat over A, then also the quotient
${}_{s} {{{\mathcal H}}}$
is flat over A, then also the quotient
![]() ${I}_{(i)}$
of a normal Hopf ideal I admits both a left and a right
${I}_{(i)}$
of a normal Hopf ideal I admits both a left and a right
![]() ${\mathcal H}$
-comodule structure as above.
${\mathcal H}$
-comodule structure as above.
4.3.3 The space of invariants
Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid, and let
$(A, {\mathcal H})$
be a commutative Hopf algebroid, and let
![]() $I \subseteq {\mathcal H}$
be a normal Hopf ideal. Denote by
$I \subseteq {\mathcal H}$
be a normal Hopf ideal. Denote by
![]() $\tilde {\pi } \colon {\mathcal H} \to {{\mathcal H}}_{(i)}/{I}_{(i)}$
the composition of the canonical projection
$\tilde {\pi } \colon {\mathcal H} \to {{\mathcal H}}_{(i)}/{I}_{(i)}$
the composition of the canonical projection
![]() $\pi \colon {\mathcal H} \to {\mathcal H}/I$
with the isomorphism
$\pi \colon {\mathcal H} \to {\mathcal H}/I$
with the isomorphism
![]() ${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
. Since this leads to a morphism of Hopf algebroids, we have an induced
${\mathcal H}/I \cong {{\mathcal H}}_{(i)}/{I}_{(i)}$
. Since this leads to a morphism of Hopf algebroids, we have an induced
![]() ${{\mathcal H}}_{(i)}/{I}_{(i)}$
-comodule structure on
${{\mathcal H}}_{(i)}/{I}_{(i)}$
-comodule structure on
![]() ${\mathcal H}$
as in Section 3, given by
${\mathcal H}$
as in Section 3, given by
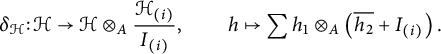 $$ \begin{align} \delta_{{\mathcal H}} \colon {\mathcal H} \to {\mathcal H}\otimes_{A} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}}, \qquad h \mapsto \sum h_1\otimes_{A} \left(\overline{h_2} + {I}_{(i)}\right). \end{align} $$
$$ \begin{align} \delta_{{\mathcal H}} \colon {\mathcal H} \to {\mathcal H}\otimes_{A} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}}, \qquad h \mapsto \sum h_1\otimes_{A} \left(\overline{h_2} + {I}_{(i)}\right). \end{align} $$
In this way,
![]() $({\mathcal H}, s)$
becomes a right
$({\mathcal H}, s)$
becomes a right
![]() ${{\mathcal H}}_{(i)}/{I}_{(i)}$
-comodule algebra. Let us denote its coinvariant subalgebra by
${{\mathcal H}}_{(i)}/{I}_{(i)}$
-comodule algebra. Let us denote its coinvariant subalgebra by
for the sake of simplicity.
Remark 4.19 Notice that the coaction (4.6) corresponds to the action described in (4.1). Namely, denote by
![]() $\tilde {\eta }$
the composition of
$\tilde {\eta }$
the composition of
![]() $A \xrightarrow {\eta } {{\mathcal H}}_{(i)}/{I}_{(i)} \cong {\mathcal H}/I$
and, for a given ring R, consider the normal subgroupoid
$A \xrightarrow {\eta } {{\mathcal H}}_{(i)}/{I}_{(i)} \cong {\mathcal H}/I$
and, for a given ring R, consider the normal subgroupoid
![]() $\mathscr {G}_{{\mathcal H}/I}(R)$
of
$\mathscr {G}_{{\mathcal H}/I}(R)$
of
![]() $\mathscr {G}_{\mathcal H}(R)$
. In this framework, the action (4.1) is given by
$\mathscr {G}_{\mathcal H}(R)$
. In this framework, the action (4.1) is given by
By using the natural isomorphism
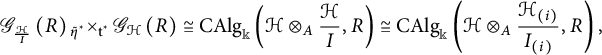
Analogously, the left
![]() ${{\mathcal H}}_{(i)}/{I}_{(i)}$
-coaction on
${{\mathcal H}}_{(i)}/{I}_{(i)}$
-coaction on
![]() ${\mathcal H}$
, which corresponds to the right action of
${\mathcal H}$
, which corresponds to the right action of
![]() $\mathscr {G}_{{\mathcal H}/I}(R)$
on
$\mathscr {G}_{{\mathcal H}/I}(R)$
on
![]() $\mathscr {G}_{\mathcal H}(R)$
from the end of Section 4.1.3, is given by
$\mathscr {G}_{\mathcal H}(R)$
from the end of Section 4.1.3, is given by
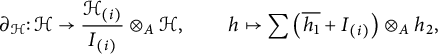 $$ \begin{align*} \partial_{{\mathcal H}} \colon {\mathcal H} \to {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {\mathcal H}, \qquad h \mapsto \sum \left(\overline{h_1} + {I}_{(i)}\right) \otimes_{A} h_2, \end{align*} $$
$$ \begin{align*} \partial_{{\mathcal H}} \colon {\mathcal H} \to {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {\mathcal H}, \qquad h \mapsto \sum \left(\overline{h_1} + {I}_{(i)}\right) \otimes_{A} h_2, \end{align*} $$
which provides a structure of left
![]() ${{\mathcal H}}_{(i)}/{I}_{(i)}$
-comodule algebra on
${{\mathcal H}}_{(i)}/{I}_{(i)}$
-comodule algebra on
![]() $({\mathcal H}, t)$
. Its coinvariant subalgebra is given by
$({\mathcal H}, t)$
. Its coinvariant subalgebra is given by
The key properties of these subalgebras are collected in the forthcoming lemmata.
Lemma 4.20 Let I be a normal Hopf ideal of
![]() $(A, {\mathcal H})$
. Then the subalgebras
$(A, {\mathcal H})$
. Then the subalgebras
![]() $s (A)$
and
$s (A)$
and
![]() $t (A)$
are contained in both
$t (A)$
are contained in both
![]() ${{{\mathcal H}}{}^{I}}$
and
${{{\mathcal H}}{}^{I}}$
and
![]() ${{}^{I}{{\mathcal H}}}$
. Furthermore, the antipode
${{}^{I}{{\mathcal H}}}$
. Furthermore, the antipode
![]() ${\mathcal S}$
establishes an isomorphism of A-bimodules
${\mathcal S}$
establishes an isomorphism of A-bimodules
![]() ${\mathcal S} \colon {{{\mathcal H}}{}^{I}}\to {{}^{I}{{\mathcal H}}}$
.
${\mathcal S} \colon {{{\mathcal H}}{}^{I}}\to {{}^{I}{{\mathcal H}}}$
.
Proof We only show that
![]() $t(A) \subseteq {{{\mathcal H}}{}^{I}}$
, since the other property is analogous. For every
$t(A) \subseteq {{{\mathcal H}}{}^{I}}$
, since the other property is analogous. For every
![]() $a \in A$
, we have
$a \in A$
, we have
by (NI1), and hence
![]() $t(a) \in {{{\mathcal H}}{}^{I}}$
. Concerning the second claim, if
$t(a) \in {{{\mathcal H}}{}^{I}}$
. Concerning the second claim, if
![]() $h \in {{{\mathcal H}}{}^{I}}$
, then
$h \in {{{\mathcal H}}{}^{I}}$
, then
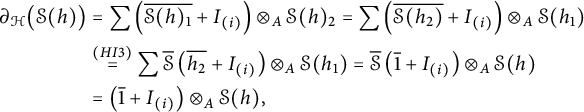 $$ \begin{align*} \partial_{\mathcal H}\big({\mathcal S}(h)\big) & = \sum \left(\overline{{\mathcal S}(h)_1} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h)_2 = \sum \left(\overline{{\mathcal S}(h_2)} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h_1) \\ & \stackrel{(HI3)}{=} \sum \overline{{\mathcal S}}\left(\overline{h_2} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h_1) = \overline{{\mathcal S}}\left(\overline{1} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h) \\ & = \left(\overline{1} + {I}_{(i)} \right)\otimes_{A} {\mathcal S}(h), \end{align*} $$
$$ \begin{align*} \partial_{\mathcal H}\big({\mathcal S}(h)\big) & = \sum \left(\overline{{\mathcal S}(h)_1} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h)_2 = \sum \left(\overline{{\mathcal S}(h_2)} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h_1) \\ & \stackrel{(HI3)}{=} \sum \overline{{\mathcal S}}\left(\overline{h_2} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h_1) = \overline{{\mathcal S}}\left(\overline{1} + {I}_{(i)}\right) \otimes_{A} {\mathcal S}(h) \\ & = \left(\overline{1} + {I}_{(i)} \right)\otimes_{A} {\mathcal S}(h), \end{align*} $$
whence
![]() ${\mathcal S}(h) \in {{}^{I}{{\mathcal H}}}$
. Similarly, one proves that if
${\mathcal S}(h) \in {{}^{I}{{\mathcal H}}}$
. Similarly, one proves that if
![]() $h \in {{}^{I}{{\mathcal H}}}$
, then
$h \in {{}^{I}{{\mathcal H}}}$
, then
![]() ${\mathcal S}(h) \in {{{\mathcal H}}{}^{I}}$
.
${\mathcal S}(h) \in {{{\mathcal H}}{}^{I}}$
.
Lemma 4.21 Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid, and let I be a normal Hopf ideal in
$(A, {\mathcal H})$
be a commutative Hopf algebroid, and let I be a normal Hopf ideal in
![]() $(A, {\mathcal H})$
. Then
$(A, {\mathcal H})$
. Then
![]() ${{{\mathcal H}}{}^{I}} = {{}^{I}{{\mathcal H}}}$
as subalgebras of
${{{\mathcal H}}{}^{I}} = {{}^{I}{{\mathcal H}}}$
as subalgebras of
![]() ${\mathcal H}$
.
${\mathcal H}$
.
Proof We find inspiration from [Reference Takeuchi36, Lemma 4.4]. First of all, consider the A-bilinear morphism
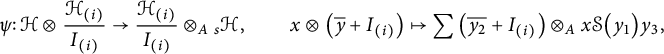 $$ \begin{align*}\psi \colon {\mathcal H} \otimes_{} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \to {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {}_{s} {{{\mathcal H}}}, \qquad x \otimes_{} \big(\overline{y} + {I}_{(i)}\big) \mapsto \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3,\end{align*} $$
$$ \begin{align*}\psi \colon {\mathcal H} \otimes_{} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \to {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {}_{s} {{{\mathcal H}}}, \qquad x \otimes_{} \big(\overline{y} + {I}_{(i)}\big) \mapsto \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3,\end{align*} $$
where the A-bilinearity is expressed by
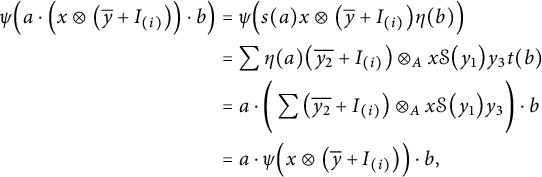 $$ \begin{align*} \psi\Big(a \cdot \Big(x \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\Big)\cdot b\Big) & = \psi\Big(s(a)x \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\eta(b)\Big) \\ & = \sum \eta(a)\big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3t(b) \\ & = a\cdot\bigg( \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3\bigg)\cdot b \\ & = a \cdot \psi\Big(x \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\Big)\cdot b, \end{align*} $$
$$ \begin{align*} \psi\Big(a \cdot \Big(x \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\Big)\cdot b\Big) & = \psi\Big(s(a)x \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\eta(b)\Big) \\ & = \sum \eta(a)\big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3t(b) \\ & = a\cdot\bigg( \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3\bigg)\cdot b \\ & = a \cdot \psi\Big(x \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\Big)\cdot b, \end{align*} $$
for all
![]() $a,b \in A$
,
$a,b \in A$
,
![]() $x,y \in {\mathcal H}$
. It satisfies
$x,y \in {\mathcal H}$
. It satisfies
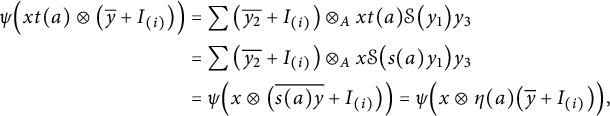 $$ \begin{align*} \psi\Big(xt(a) \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\Big) & = \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} xt(a){\mathcal S}\big(y_1\big)y_3 \\ & = \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(s(a)y_1\big)y_3 \\ & = \psi\Big(x \otimes_{} \big(\overline{s(a)y} + {I}_{(i)}\big)\Big) = \psi\Big(x \otimes_{} \eta(a)\big(\overline{y} + {I}_{(i)}\big)\Big), \end{align*} $$
$$ \begin{align*} \psi\Big(xt(a) \otimes_{} \big(\overline{y} + {I}_{(i)}\big)\Big) & = \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} xt(a){\mathcal S}\big(y_1\big)y_3 \\ & = \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(s(a)y_1\big)y_3 \\ & = \psi\Big(x \otimes_{} \big(\overline{s(a)y} + {I}_{(i)}\big)\Big) = \psi\Big(x \otimes_{} \eta(a)\big(\overline{y} + {I}_{(i)}\big)\Big), \end{align*} $$
for all
![]() $a \in A$
,
$a \in A$
,
![]() $x,y \in {\mathcal H}$
. Therefore,
$x,y \in {\mathcal H}$
. Therefore,
![]() $\psi $
factors uniquely through the tensor product over A, inducing an A-bilinear morphism
$\psi $
factors uniquely through the tensor product over A, inducing an A-bilinear morphism
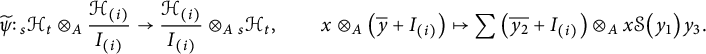 $$ \begin{align*}\widetilde{\psi} \colon {}_{s} {{\mathcal H}}{}_{t} \otimes_{A} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \to {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {}_{s} {{\mathcal H}}{}_{t}, \qquad x \otimes_{A} \big(\overline{y} + {I}_{(i)}\big) \mapsto \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3.\end{align*} $$
$$ \begin{align*}\widetilde{\psi} \colon {}_{s} {{\mathcal H}}{}_{t} \otimes_{A} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \to {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {}_{s} {{\mathcal H}}{}_{t}, \qquad x \otimes_{A} \big(\overline{y} + {I}_{(i)}\big) \mapsto \sum \big(\overline{y_2} + {I}_{(i)} \big)\otimes_{A} x{\mathcal S}\big(y_1\big)y_3.\end{align*} $$
Take an element
![]() $h \in {{{\mathcal H}}{}^{I}}$
, so that
$h \in {{{\mathcal H}}{}^{I}}$
, so that
![]() $\sum h_1 \otimes _{A} \left ( \overline {h_2} + {I}_{(i)} \right ) = h\otimes _{A} \left (\overline {1} + {I}_{(i)} \right )$
in
$\sum h_1 \otimes _{A} \left ( \overline {h_2} + {I}_{(i)} \right ) = h\otimes _{A} \left (\overline {1} + {I}_{(i)} \right )$
in
![]() ${\mathcal H}\otimes _{A}{{\mathcal H}}_{(i)}/{I}_{(i)}$
. By applying
${\mathcal H}\otimes _{A}{{\mathcal H}}_{(i)}/{I}_{(i)}$
. By applying
![]() $\widetilde {\psi }$
to both sides of the latter identity, we get
$\widetilde {\psi }$
to both sides of the latter identity, we get
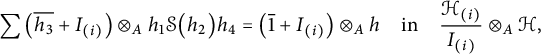 $$ \begin{align*} \sum \left( \overline{h_3} + {I}_{(i)} \right) \otimes_{A} h_1{\mathcal S}\big(h_2\big)h_4 = \left(\overline{1} + {I}_{(i)} \right) \otimes_{A} h \quad \text{in} \quad {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {\mathcal H}, \end{align*} $$
$$ \begin{align*} \sum \left( \overline{h_3} + {I}_{(i)} \right) \otimes_{A} h_1{\mathcal S}\big(h_2\big)h_4 = \left(\overline{1} + {I}_{(i)} \right) \otimes_{A} h \quad \text{in} \quad {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {\mathcal H}, \end{align*} $$
that is to say,
![]() $\sum \left ( \overline {h_1} + {I}_{(i)} \right ) \otimes _{A} h_2 = \left (\overline {1} + {I}_{(i)} \right ) \otimes _{A} h$
, and hence
$\sum \left ( \overline {h_1} + {I}_{(i)} \right ) \otimes _{A} h_2 = \left (\overline {1} + {I}_{(i)} \right ) \otimes _{A} h$
, and hence
![]() $h \in {{}^{I}{{\mathcal H}}}$
. The other inclusion is proved similarly by using the morphism
$h \in {{}^{I}{{\mathcal H}}}$
. The other inclusion is proved similarly by using the morphism
 $$ \begin{align*}{\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {}_{s} {{\mathcal H}}{}_{t} \to {}_{s} {{\mathcal H}}{}_{t} \otimes_{A} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}}, \qquad \big(\overline{x} + {I}_{(i)}\big) \otimes_{A} y \mapsto \sum x_1{\mathcal S}\big(x_3\big)y \otimes_{A} \big(\overline{x_2} + {I}_{(i)} \big). \end{align*} $$
$$ \begin{align*}{\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}} \otimes_{A} {}_{s} {{\mathcal H}}{}_{t} \to {}_{s} {{\mathcal H}}{}_{t} \otimes_{A} {\displaystyle \frac{{{\mathcal H}}_{(i)}}{{I}_{(i)}}}, \qquad \big(\overline{x} + {I}_{(i)}\big) \otimes_{A} y \mapsto \sum x_1{\mathcal S}\big(x_3\big)y \otimes_{A} \big(\overline{x_2} + {I}_{(i)} \big). \end{align*} $$
As we have seen in Proposition 4.17, for every commutative
![]() $\Bbbk $
-algebra R, we have that
$\Bbbk $
-algebra R, we have that
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}/I}(R)\big )$
is a normal subgroupoid of
$\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}/I}(R)\big )$
is a normal subgroupoid of
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}}(R)\big )$
, and hence, by Lemma 4.5, we can consider the extension
$\big (\mathscr {G}_A(R),\mathscr {G}_{{\mathcal H}}(R)\big )$
, and hence, by Lemma 4.5, we can consider the extension
![]() $\mathscr {G}_{{\mathcal H}/I}(R) \hookrightarrow \mathscr {G}_{\mathcal H}(R) \twoheadrightarrow \mathscr {G}_{\mathcal H}(R)/\mathscr {G}_{{\mathcal H}/I}(R)$
. As a matter of notation, set
$\mathscr {G}_{{\mathcal H}/I}(R) \hookrightarrow \mathscr {G}_{\mathcal H}(R) \twoheadrightarrow \mathscr {G}_{\mathcal H}(R)/\mathscr {G}_{{\mathcal H}/I}(R)$
. As a matter of notation, set
![]() $\phi \colon {\mathcal H}^I \to {\mathcal H}$
for the canonical inclusion and
$\phi \colon {\mathcal H}^I \to {\mathcal H}$
for the canonical inclusion and
![]() $\Phi _R \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H}, R) \to \mathrm {CAlg}_{\Bbbk }({\mathcal H}^I, R)$
for its dual
$\Phi _R \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H}, R) \to \mathrm {CAlg}_{\Bbbk }({\mathcal H}^I, R)$
for its dual
![]() $\phi ^*$
.
$\phi ^*$
.
Lemma 4.22 Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid, and let
$(A, {\mathcal H})$
be a commutative Hopf algebroid, and let
![]() $I\subseteq {\mathcal H}$
be a normal Hopf ideal. Then there is a canonical morphism
$I\subseteq {\mathcal H}$
be a normal Hopf ideal. Then there is a canonical morphism
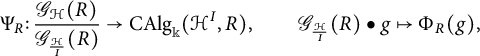 $$ \begin{align} \Psi_R \colon {\displaystyle\frac{\mathscr{G}_{\mathcal H}(R)}{\mathscr{G}_{\frac{{\mathcal H}}{I}}(R)}} \to \mathrm{CAlg}_{\Bbbk}({{{\mathcal H}}{}^{I}}, R), \qquad \mathscr{G}_{\frac{{\mathcal H}}{I}}(R)\bullet g \mapsto \Phi_R(g), \end{align} $$
$$ \begin{align} \Psi_R \colon {\displaystyle\frac{\mathscr{G}_{\mathcal H}(R)}{\mathscr{G}_{\frac{{\mathcal H}}{I}}(R)}} \to \mathrm{CAlg}_{\Bbbk}({{{\mathcal H}}{}^{I}}, R), \qquad \mathscr{G}_{\frac{{\mathcal H}}{I}}(R)\bullet g \mapsto \Phi_R(g), \end{align} $$
which is natural in
![]() $R \in \mathrm {CAlg}_{\Bbbk }$
.
$R \in \mathrm {CAlg}_{\Bbbk }$
.
Proof Consider
![]() $\Psi _R$
as in the statement and observe that if
$\Psi _R$
as in the statement and observe that if
![]() $\mathscr {G}_{{\mathcal H}/I}(R)\bullet g = \mathscr {G}_{{\mathcal H}/I}(R)\bullet g'$
, then there exists
$\mathscr {G}_{{\mathcal H}/I}(R)\bullet g = \mathscr {G}_{{\mathcal H}/I}(R)\bullet g'$
, then there exists
![]() $f \in \mathscr {G}_{{\mathcal H}/I}(R)$
such that
$f \in \mathscr {G}_{{\mathcal H}/I}(R)$
such that
![]() $(f \circ \pi ) \bullet g = g'$
. Therefore, for every
$(f \circ \pi ) \bullet g = g'$
. Therefore, for every
![]() ${u \in {\mathcal H}^I}$
,
${u \in {\mathcal H}^I}$
,
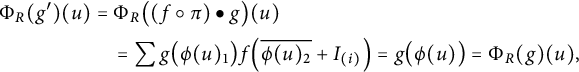 $$ \begin{align*}\Phi_R(g')(u) &= \Phi_R \big((f \circ \pi) \bullet g\big)(u) \\&\quad= \sum g\big(\phi(u)_1\big)f\Big(\overline{\phi(u)_2} + {I}_{(i)}\Big) = g\big(\phi(u)\big) = \Phi_R(g)(u),\end{align*} $$
$$ \begin{align*}\Phi_R(g')(u) &= \Phi_R \big((f \circ \pi) \bullet g\big)(u) \\&\quad= \sum g\big(\phi(u)_1\big)f\Big(\overline{\phi(u)_2} + {I}_{(i)}\Big) = g\big(\phi(u)\big) = \Phi_R(g)(u),\end{align*} $$
since
![]() $\phi $
is just the inclusion. Thus,
$\phi $
is just the inclusion. Thus,
![]() $\Psi _R$
is well defined and it is clearly natural.
$\Psi _R$
is well defined and it is clearly natural.
4.3 The correspondence for commutative Hopf algebroids
We fix a commutative Hopf algebroid
![]() $(A, {\mathcal H})$
which we assume to be flat as left A-module (that is, the extension
$(A, {\mathcal H})$
which we assume to be flat as left A-module (that is, the extension
![]() $s \colon A \to {\mathcal H}$
is flat). In this case
$s \colon A \to {\mathcal H}$
is flat). In this case
![]() $t \colon A \to {\mathcal H}$
is also flat, thanks to the antipode, and both extension
$t \colon A \to {\mathcal H}$
is also flat, thanks to the antipode, and both extension
![]() $s $
and
$s $
and
![]() $t $
are faithfully flat (because both are split monomorphisms of modules over the base algebra). Also, since A and
$t $
are faithfully flat (because both are split monomorphisms of modules over the base algebra). Also, since A and
![]() ${\mathcal H}$
are commutative algebras, then
${\mathcal H}$
are commutative algebras, then
![]() ${{\mathcal H}}{}_{t}$
being A-flat is equivalent to
${{\mathcal H}}{}_{t}$
being A-flat is equivalent to
![]() ${}_{t} {{\mathcal H}}$
being A-flat.
${}_{t} {{\mathcal H}}$
being A-flat.
Proposition 4.23 If
![]() $(A,{\mathcal H})$
is a commutative Hopf algebroid and
$(A,{\mathcal H})$
is a commutative Hopf algebroid and
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat, then we have a well-defined inclusion-preserving bijective correspondence
${}_{s} {{{\mathcal H}}}$
is A-flat, then we have a well-defined inclusion-preserving bijective correspondence

Proof Since all the algebras involved are commutative, it follows from [Reference Janelidze and Tholen23, Corollary 5.4] that a
![]() $\Bbbk $
-algebra morphism
$\Bbbk $
-algebra morphism
![]() $B \to {\mathcal H}$
is pure as a morphism of B-modules if and only if the extension-of-scalars functor
$B \to {\mathcal H}$
is pure as a morphism of B-modules if and only if the extension-of-scalars functor
![]() ${\mathcal H} \otimes _{B} -$
is comonadic. Thus, it is enough to show that the additional condition in Theorem 3.15, which involves the translation map
${\mathcal H} \otimes _{B} -$
is comonadic. Thus, it is enough to show that the additional condition in Theorem 3.15, which involves the translation map
![]() $\gamma $
, is always satisfied in this setting. Recall from (4.2) that
$\gamma $
, is always satisfied in this setting. Recall from (4.2) that
![]() $\gamma $
is explicit given by
$\gamma $
is explicit given by
![]() $\big ({\mathcal H} \otimes _{A} {\mathcal S}\big ) \circ \Delta $
. If
$\big ({\mathcal H} \otimes _{A} {\mathcal S}\big ) \circ \Delta $
. If
![]() $B\subseteq {\mathcal H}$
is a right
$B\subseteq {\mathcal H}$
is a right
![]() ${\mathcal H}$
-coideal A-subalgebra via t, then the left-hand side square of the following diagram is commutative:
${\mathcal H}$
-coideal A-subalgebra via t, then the left-hand side square of the following diagram is commutative:
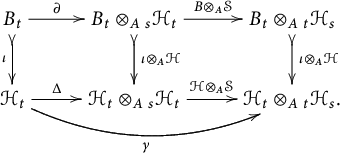
Since the right-hand side square is clearly commutative, we have that the condition
![]() $\gamma (B) \subseteq B \otimes _{A} {\mathcal H}$
is satisfied. Therefore, the conclusion follows from Theorem 3.15.
$\gamma (B) \subseteq B \otimes _{A} {\mathcal H}$
is satisfied. Therefore, the conclusion follows from Theorem 3.15.
Proposition 4.24 Let
![]() $(A,{\mathcal H})$
be a commutative Hopf algebroid such that
$(A,{\mathcal H})$
be a commutative Hopf algebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat. Suppose that
${}_{s} {{{\mathcal H}}}$
is A-flat. Suppose that
![]() ${\mathcal K}\subseteq {\mathcal H}$
is a sub-Hopf algebroid, over the same base A, such that
${\mathcal K}\subseteq {\mathcal H}$
is a sub-Hopf algebroid, over the same base A, such that
![]() ${\mathcal H}_{\mathcal K}$
is pure. Then
${\mathcal H}_{\mathcal K}$
is pure. Then
![]() ${\mathcal H}{\mathcal K}^+$
is a normal Hopf ideal in
${\mathcal H}{\mathcal K}^+$
is a normal Hopf ideal in
![]() ${\mathcal H}$
such that
${\mathcal H}$
such that
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H}{\mathcal K}^+}}}$
.
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H}{\mathcal K}^+}}}$
.
Proof Since it is clear that
![]() ${\mathcal K}$
is a right
${\mathcal K}$
is a right
![]() ${\mathcal H}$
-comodule A-subalgebra of
${\mathcal H}$
-comodule A-subalgebra of
![]() ${\mathcal H}$
via t, we already know from Proposition 4.23 that
${\mathcal H}$
via t, we already know from Proposition 4.23 that
![]() ${\mathcal H}{\mathcal K}^+$
is a (two-sided) ideal of
${\mathcal H}{\mathcal K}^+$
is a (two-sided) ideal of
![]() ${\mathcal H}$
which satisfies (HI1) and (HI2), and that
${\mathcal H}$
which satisfies (HI1) and (HI2), and that
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H}{\mathcal K}^+}}}$
. Concerning (HI3), it is easily checked that
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{{\mathcal H}{\mathcal K}^+}}}$
. Concerning (HI3), it is easily checked that
because
![]() ${\mathcal K}$
is a sub-Hopf algebroid (whence
${\mathcal K}$
is a sub-Hopf algebroid (whence
![]() ${\mathcal S}({\mathcal K})\subseteq {\mathcal K}$
). Therefore,
${\mathcal S}({\mathcal K})\subseteq {\mathcal K}$
). Therefore,
![]() ${\mathcal H}{\mathcal K}^+$
is a Hopf ideal. In addition, since for every
${\mathcal H}{\mathcal K}^+$
is a Hopf ideal. In addition, since for every
![]() $a \in A$
we have that
$a \in A$
we have that
![]() $s(a) - t(a) \in {\mathcal K}^+$
, we also have that
$s(a) - t(a) \in {\mathcal K}^+$
, we also have that
![]() $\langle s-t \rangle \subseteq {\mathcal H}{\mathcal K}^+$
, which is (NI1). To check that (NI2) also holds, let us begin by observing that
$\langle s-t \rangle \subseteq {\mathcal H}{\mathcal K}^+$
, which is (NI1). To check that (NI2) also holds, let us begin by observing that
![]() $A \cong {\mathcal K}/{\mathcal K}^+$
has a
$A \cong {\mathcal K}/{\mathcal K}^+$
has a
![]() $({\mathcal K},A)$
-bimodule structure via the regular right A-action
$({\mathcal K},A)$
-bimodule structure via the regular right A-action
![]() $x\cdot a = \varepsilon (x)a$
for all
$x\cdot a = \varepsilon (x)a$
for all
![]() $a \in A$
,
$a \in A$
,
![]() $x \in {\mathcal K}$
. Therefore,
$x \in {\mathcal K}$
. Therefore,
via
![]() $\big (x + {\mathcal H}{\mathcal K}^+\big ) \otimes _{A} y \mapsto x \otimes _{{\mathcal K}} y$
. Denote this latter isomorphism by
$\big (x + {\mathcal H}{\mathcal K}^+\big ) \otimes _{A} y \mapsto x \otimes _{{\mathcal K}} y$
. Denote this latter isomorphism by
![]() $\varphi \colon {\mathcal H}/{\mathcal H}{\mathcal K}^+ \otimes _{A} {\mathcal H} \to {\mathcal H} \otimes _{{\mathcal K}} {{}_{s\varepsilon }{\mathcal H}}$
. In view of the flatness of
$\varphi \colon {\mathcal H}/{\mathcal H}{\mathcal K}^+ \otimes _{A} {\mathcal H} \to {\mathcal H} \otimes _{{\mathcal K}} {{}_{s\varepsilon }{\mathcal H}}$
. In view of the flatness of
![]() ${\mathcal H}$
over A, an element
${\mathcal H}$
over A, an element
![]() $\sum _i \overline {x_i} \otimes _{A} y_i$
in
$\sum _i \overline {x_i} \otimes _{A} y_i$
in
![]() ${{\mathcal H}}_{(i)} \otimes _{A} {\mathcal H}$
belongs to
${{\mathcal H}}_{(i)} \otimes _{A} {\mathcal H}$
belongs to
![]() ${({\mathcal H}{\mathcal K}^+)}_{(i)} \otimes _{A} {\mathcal H}$
if and only if it belongs to the kernel of the canonical projection
${({\mathcal H}{\mathcal K}^+)}_{(i)} \otimes _{A} {\mathcal H}$
if and only if it belongs to the kernel of the canonical projection
![]() ${\tilde {\pi }}_{(i)} \otimes _{A} {\mathcal H} \colon {{\mathcal H}}_{(i)} \otimes _{A} {\mathcal H} \to {\mathcal H}/{\mathcal H}{\mathcal K}^+ \otimes _{A} {\mathcal H}$
. If
${\tilde {\pi }}_{(i)} \otimes _{A} {\mathcal H} \colon {{\mathcal H}}_{(i)} \otimes _{A} {\mathcal H} \to {\mathcal H}/{\mathcal H}{\mathcal K}^+ \otimes _{A} {\mathcal H}$
. If
![]() $\sum _i \overline {h_ix_i} \in {({\mathcal H}{\mathcal K}^+)}_{(i)}$
, then
$\sum _i \overline {h_ix_i} \in {({\mathcal H}{\mathcal K}^+)}_{(i)}$
, then
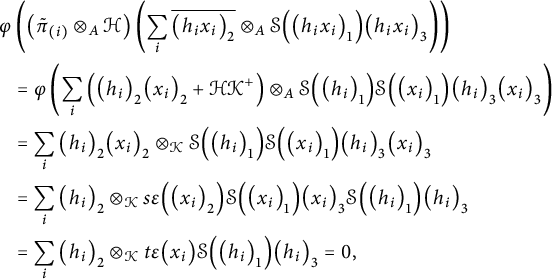 $$ \begin{align*} \varphi & \left(\left({\tilde{\pi}}_{(i)} \otimes_{A} {\mathcal H}\right)\left(\sum_i \overline{\big(h_ix_i\big)_2} \otimes_{A} {\mathcal S}\Big(\big(h_ix_i\big)_1\Big)\big(h_ix_i\big)_3\right)\right) \\ & = \varphi\left(\sum_i \Big(\big(h_i\big)_2\big(x_i\big)_2 + {\mathcal H}{\mathcal K}^+\Big) \otimes_{A} {\mathcal S}\Big(\big(h_i\big)_1\Big){\mathcal S}\Big(\big(x_i\big)_1\Big)\big(h_i\big)_3\big(x_i\big)_3\right) \\ & = \sum_i \big(h_i\big)_2\big(x_i\big)_2 \otimes_{{\mathcal K}} {\mathcal S}\Big(\big(h_i\big)_1\Big){\mathcal S}\Big(\big(x_i\big)_1\Big)\big(h_i\big)_3\big(x_i\big)_3 \\ & = \sum_i \big(h_i\big)_2 \otimes_{{\mathcal K}} s\varepsilon\Big(\big(x_i\big)_2\Big){\mathcal S}\Big(\big(x_i\big)_1\Big)\big(x_i\big)_3{\mathcal S}\Big(\big(h_i\big)_1\Big)\big(h_i\big)_3 \\ & = \sum_i \big(h_i\big)_2 \otimes_{{\mathcal K}} t\varepsilon\big(x_i\big){\mathcal S}\Big(\big(h_i\big)_1\Big)\big(h_i\big)_3 = 0, \end{align*} $$
$$ \begin{align*} \varphi & \left(\left({\tilde{\pi}}_{(i)} \otimes_{A} {\mathcal H}\right)\left(\sum_i \overline{\big(h_ix_i\big)_2} \otimes_{A} {\mathcal S}\Big(\big(h_ix_i\big)_1\Big)\big(h_ix_i\big)_3\right)\right) \\ & = \varphi\left(\sum_i \Big(\big(h_i\big)_2\big(x_i\big)_2 + {\mathcal H}{\mathcal K}^+\Big) \otimes_{A} {\mathcal S}\Big(\big(h_i\big)_1\Big){\mathcal S}\Big(\big(x_i\big)_1\Big)\big(h_i\big)_3\big(x_i\big)_3\right) \\ & = \sum_i \big(h_i\big)_2\big(x_i\big)_2 \otimes_{{\mathcal K}} {\mathcal S}\Big(\big(h_i\big)_1\Big){\mathcal S}\Big(\big(x_i\big)_1\Big)\big(h_i\big)_3\big(x_i\big)_3 \\ & = \sum_i \big(h_i\big)_2 \otimes_{{\mathcal K}} s\varepsilon\Big(\big(x_i\big)_2\Big){\mathcal S}\Big(\big(x_i\big)_1\Big)\big(x_i\big)_3{\mathcal S}\Big(\big(h_i\big)_1\Big)\big(h_i\big)_3 \\ & = \sum_i \big(h_i\big)_2 \otimes_{{\mathcal K}} t\varepsilon\big(x_i\big){\mathcal S}\Big(\big(h_i\big)_1\Big)\big(h_i\big)_3 = 0, \end{align*} $$
which entails that
![]() $\sum _i \overline {\big (h_ix_i\big )_2} \otimes _{A} {\mathcal S}\Big (\big (h_ix_i\big )_1\Big )\big (h_ix_i\big )_3 \in {({\mathcal H}{\mathcal K}^+)}_{(i)} \otimes _{A} {\mathcal H}$
, as prescribed by (NI2).
$\sum _i \overline {\big (h_ix_i\big )_2} \otimes _{A} {\mathcal S}\Big (\big (h_ix_i\big )_1\Big )\big (h_ix_i\big )_3 \in {({\mathcal H}{\mathcal K}^+)}_{(i)} \otimes _{A} {\mathcal H}$
, as prescribed by (NI2).
Proposition 4.25 Let I be a normal Hopf ideal of a commutative Hopf algebroid
![]() $(A,{\mathcal H})$
such that
$(A,{\mathcal H})$
such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat and
${}_{s} {{{\mathcal H}}}$
is A-flat and
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
. Then the pair
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
. Then the pair
![]() $\Big (A, {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\Big )$
is a sub-Hopf algebroid of
$\Big (A, {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\Big )$
is a sub-Hopf algebroid of
![]() $(A,{\mathcal H})$
.
$(A,{\mathcal H})$
.
Proof Set
![]() , which in (4.7) we denoted by
, which in (4.7) we denoted by
![]() ${{}^{I}{{\mathcal H}}}$
, for the sake of brevity. By Proposition 4.23, we already know that
${{}^{I}{{\mathcal H}}}$
, for the sake of brevity. By Proposition 4.23, we already know that
![]() ${\mathcal K}$
is a right
${\mathcal K}$
is a right
![]() ${\mathcal H}$
-comodule subalgebra of
${\mathcal H}$
-comodule subalgebra of
![]() ${\mathcal H}$
via t. By Lemmas 4.20 and 4.21, we also know that
${\mathcal H}$
via t. By Lemmas 4.20 and 4.21, we also know that
![]() ${\mathcal K} = {{{\mathcal H}}{}^{I}}$
, that s takes values in
${\mathcal K} = {{{\mathcal H}}{}^{I}}$
, that s takes values in
![]() ${\mathcal K}$
, and that
${\mathcal K}$
, and that
![]() ${\mathcal S}\big ({\mathcal K}\big ) \subseteq {\mathcal K}$
. Therefore, by adapting Proposition 3.4,
${\mathcal S}\big ({\mathcal K}\big ) \subseteq {\mathcal K}$
. Therefore, by adapting Proposition 3.4,
![]() ${\mathcal K}$
is also a left
${\mathcal K}$
is also a left
![]() ${\mathcal H}$
-comodule subalgebra of
${\mathcal H}$
-comodule subalgebra of
![]() ${\mathcal H}$
via s.
${\mathcal H}$
via s.
Since
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${\mathcal K}$
and flat over A,
${\mathcal K}$
and flat over A,
![]() ${\mathcal K}$
is flat over A (see Corollary 2.3) and so
${\mathcal K}$
is flat over A (see Corollary 2.3) and so
Hence, in view of the foregoing observations, we only need to check that
![]() $\Delta ({\mathcal K})$
, which we know is contained in
$\Delta ({\mathcal K})$
, which we know is contained in
![]() $\big ({\mathcal K} \otimes _{A} {\mathcal H}\big ) \cap \big ({\mathcal H} \otimes _{A} {\mathcal K}\big )$
, is contained in
$\big ({\mathcal K} \otimes _{A} {\mathcal H}\big ) \cap \big ({\mathcal H} \otimes _{A} {\mathcal K}\big )$
, is contained in
![]() ${\mathcal K} \otimes _{A} {\mathcal K}$
. To this aim, denote by
${\mathcal K} \otimes _{A} {\mathcal K}$
. To this aim, denote by
![]() $\iota \colon {\mathcal K} \to {\mathcal H}$
the canonical inclusion, which we know is pure as morphism of A-modules by Corollary 2.4. Now, in view of the fact that both
$\iota \colon {\mathcal K} \to {\mathcal H}$
the canonical inclusion, which we know is pure as morphism of A-modules by Corollary 2.4. Now, in view of the fact that both
![]() ${\mathcal H}$
and
${\mathcal H}$
and
![]() ${\mathcal K}$
are flat over A, the columns of the following diagram are monomorphisms and the rows are equalizers
${\mathcal K}$
are flat over A, the columns of the following diagram are monomorphisms and the rows are equalizers
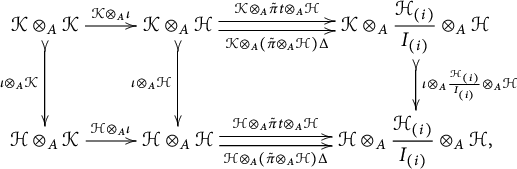
and since the diagram commutes sequentially, we can conclude that the left-hand square is a pullback square and hence that
![]() ${\mathcal K} \otimes _{A} {\mathcal K} = \big ({\mathcal K} \otimes _{A} {\mathcal H}\big ) \cap \big ({\mathcal H} \otimes _{A} {\mathcal K}\big )$
.
${\mathcal K} \otimes _{A} {\mathcal K} = \big ({\mathcal K} \otimes _{A} {\mathcal H}\big ) \cap \big ({\mathcal H} \otimes _{A} {\mathcal K}\big )$
.
Theorem 4.26 If
![]() $(A,{\mathcal H})$
is a commutative Hopf algebroid and
$(A,{\mathcal H})$
is a commutative Hopf algebroid and
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat, then we have a well-defined inclusion-preserving bijective correspondence
${}_{s} {{{\mathcal H}}}$
is A-flat, then we have a well-defined inclusion-preserving bijective correspondence

Recall that a Hopf algebroid
![]() ${\mathcal H}$
for which the base algebra A is a separable-Frobenius algebra is exactly a weak Hopf algebra. As in the above correspondence theorems the base algebra is the same for all considered sub-Hopf algebroids, these sub-Hopf algebroids are also weak sub-Hopf algebras. Examples of weak Hopf algebras arise naturally from finite groupoids. As a reality check, we now reflect on what this bijection reduces to for a simple family of commutative Hopf algebroids coming from finite groupoids in an elementary way. In this finite setting, we recover the fact that the bijection reduces to the correspondence between normal subgroupoids and quotient groupoids.
${\mathcal H}$
for which the base algebra A is a separable-Frobenius algebra is exactly a weak Hopf algebra. As in the above correspondence theorems the base algebra is the same for all considered sub-Hopf algebroids, these sub-Hopf algebroids are also weak sub-Hopf algebras. Examples of weak Hopf algebras arise naturally from finite groupoids. As a reality check, we now reflect on what this bijection reduces to for a simple family of commutative Hopf algebroids coming from finite groupoids in an elementary way. In this finite setting, we recover the fact that the bijection reduces to the correspondence between normal subgroupoids and quotient groupoids.
Example 4.27 Let
![]() $\Bbbk $
be an algebraically closed field. Throughout this example, we will assume that
$\Bbbk $
be an algebraically closed field. Throughout this example, we will assume that
![]() $\mathscr {G} = \big (\mathscr {G}_{0}, \mathscr {G}_{1}\big ) $
is a finite groupoid, meaning
$\mathscr {G} = \big (\mathscr {G}_{0}, \mathscr {G}_{1}\big ) $
is a finite groupoid, meaning
![]() $\mathscr {G}_{0}$
and
$\mathscr {G}_{0}$
and
![]() $\mathscr {G}_{1}$
are both finite sets. In this case, we can define the commutative Hopf algebroid
$\mathscr {G}_{1}$
are both finite sets. In this case, we can define the commutative Hopf algebroid
![]() $\big (\Bbbk (\mathscr {G}_{0}), \Bbbk (\mathscr {G}_{1})\big )$
of functions on the groupoid
$\big (\Bbbk (\mathscr {G}_{0}), \Bbbk (\mathscr {G}_{1})\big )$
of functions on the groupoid
![]() $\mathscr {G}$
as follows. Let
$\mathscr {G}$
as follows. Let
![]() denote the commutative algebra of functions on the set
denote the commutative algebra of functions on the set
![]() $\mathscr {G}_{0}$
which is spanned by elements of the form
$\mathscr {G}_{0}$
which is spanned by elements of the form
![]() $f_{p}$
corresponding to
$f_{p}$
corresponding to
![]() $p\in \mathscr {G}_{0}$
satisfying
$p\in \mathscr {G}_{0}$
satisfying
![]() $f_{p}.f_{p'}= \delta _{p,p'}f_{p}$
, whereas
$f_{p}.f_{p'}= \delta _{p,p'}f_{p}$
, whereas
![]() denotes the algebra of functions on the set of morphisms
denotes the algebra of functions on the set of morphisms
![]() $\mathscr {G}_{1}$
in a similar way. Hence,
$\mathscr {G}_{1}$
in a similar way. Hence,
![]() $\Bbbk (\mathscr {G}_{1})$
is generated by elements
$\Bbbk (\mathscr {G}_{1})$
is generated by elements
![]() $f_{ {g}}$
corresponding to morphisms
$f_{ {g}}$
corresponding to morphisms
![]() $ {g}\in \mathscr {G}_{1}$
and
$ {g}\in \mathscr {G}_{1}$
and
![]() $f_{ {g_{1}}}. f_{ {g_{2}}}=\delta _{ {g_{1}}, {g_{2}}} f_{ {g_{1}}}$
holds for arbitrary
$f_{ {g_{1}}}. f_{ {g_{2}}}=\delta _{ {g_{1}}, {g_{2}}} f_{ {g_{1}}}$
holds for arbitrary
![]() $g_{1},g_{2}\in \mathscr {G}_{1}$
. The Hopf algebroid structure is defined as follows:
$g_{1},g_{2}\in \mathscr {G}_{1}$
. The Hopf algebroid structure is defined as follows:
 $$ \begin{gather*} s (f_{p}) = \sum_{ {g\in \mathscr{G}_{1}}: \ \sigma( {g})=p} f_{ {g}},\quad t (f_{p}) = \sum_{ {g\in \mathscr{G}_{1}}:\ \tau ( {g})=p} f_{ {g}}, \\ \Delta ( f_{ {g}}) = \sum_{ {g_{1}}, {g_{2}}\in \mathscr{G}_{1}:\ {g_{2}}. {g_{1}}= {g}} f_{ {g_{1}}}\otimes_{A} f_{ {g_{2}}}, \\ \varepsilon ( f_{ {g}}) =\sum_{p\in \mathscr{G}_{0}} \delta_{ {g}, e({p})}f_{p}, \quad S\left( f_{ {g}}\right)= f_{ {g}^{-1}} ,\quad 1= \sum_{ {g}\in \mathscr{G}_{1}} f_{ {g}}. \end{gather*} $$
$$ \begin{gather*} s (f_{p}) = \sum_{ {g\in \mathscr{G}_{1}}: \ \sigma( {g})=p} f_{ {g}},\quad t (f_{p}) = \sum_{ {g\in \mathscr{G}_{1}}:\ \tau ( {g})=p} f_{ {g}}, \\ \Delta ( f_{ {g}}) = \sum_{ {g_{1}}, {g_{2}}\in \mathscr{G}_{1}:\ {g_{2}}. {g_{1}}= {g}} f_{ {g_{1}}}\otimes_{A} f_{ {g_{2}}}, \\ \varepsilon ( f_{ {g}}) =\sum_{p\in \mathscr{G}_{0}} \delta_{ {g}, e({p})}f_{p}, \quad S\left( f_{ {g}}\right)= f_{ {g}^{-1}} ,\quad 1= \sum_{ {g}\in \mathscr{G}_{1}} f_{ {g}}. \end{gather*} $$
Notice that, A being semisimple, every A-module is projective and hence flat.
Let us first characterize the structures in the left-hand side of the bijection in Theorem 4.26. In Example 3.6 of [Reference Ghobadi19], it was already shown that any Hopf ideal I of
![]() $\Bbbk (\mathscr {G}_{1})$
must be of the form
$\Bbbk (\mathscr {G}_{1})$
must be of the form
![]() $\Bbbk (S_1)$
for a subset
$\Bbbk (S_1)$
for a subset
![]() $S_1$
of
$S_1$
of
![]() $\mathscr {G}_{1}$
for which
$\mathscr {G}_{1}$
for which
![]() $(\mathscr {G}_{0},\mathscr {G}_{1} \setminus S_{1})$
forms a subgroupoid of
$(\mathscr {G}_{0},\mathscr {G}_{1} \setminus S_{1})$
forms a subgroupoid of
![]() $\mathscr {G}$
. If I is also normal, (NI1) implies that
$\mathscr {G}$
. If I is also normal, (NI1) implies that
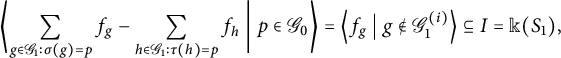 $$ \begin{align*}\left\langle \sum_{ {g\in \mathscr{G}_{1}}: \sigma( {g})=p} f_{ {g}}-\sum_{ {h\in \mathscr{G}_{1}}: \tau( {h})=p} f_{ {h}} ~\bigg\vert~ p\in\mathscr{G}_{0} \right\rangle= \left\langle f_{g} ~\big\vert~ g\notin \mathscr{G}_{1}^{(i)}\right\rangle \subseteq I=\Bbbk(S_{1}),\end{align*} $$
$$ \begin{align*}\left\langle \sum_{ {g\in \mathscr{G}_{1}}: \sigma( {g})=p} f_{ {g}}-\sum_{ {h\in \mathscr{G}_{1}}: \tau( {h})=p} f_{ {h}} ~\bigg\vert~ p\in\mathscr{G}_{0} \right\rangle= \left\langle f_{g} ~\big\vert~ g\notin \mathscr{G}_{1}^{(i)}\right\rangle \subseteq I=\Bbbk(S_{1}),\end{align*} $$
and therefore
![]() $\mathscr {G}_{1} \setminus S_{1}\subseteq \mathscr {G}^{(i)}_{1}$
. It is also easy to check that
$\mathscr {G}_{1} \setminus S_{1}\subseteq \mathscr {G}^{(i)}_{1}$
. It is also easy to check that
for any
![]() $\overline {f_{g}}\in I_{(i)}$
. Hence, (NI2) holds if and only if
$\overline {f_{g}}\in I_{(i)}$
. Hence, (NI2) holds if and only if
![]() $\mathscr {G}_{1}^{(i)}\cap S_{1}$
is closed under conjugation if and only if
$\mathscr {G}_{1}^{(i)}\cap S_{1}$
is closed under conjugation if and only if
![]() $ \mathscr {G}_{1}^{(i)}\setminus S_{1}$
is closed under conjugation; i.e., condition (NG2) holds. Hence, normal Hopf ideals
$ \mathscr {G}_{1}^{(i)}\setminus S_{1}$
is closed under conjugation; i.e., condition (NG2) holds. Hence, normal Hopf ideals
![]() $I=\Bbbk (S_{1})$
of
$I=\Bbbk (S_{1})$
of
![]() $\big (\Bbbk (\mathscr {G}_{0}), \Bbbk (\mathscr {G}_{1})\big )$
correspond to normal subgroupoids
$\big (\Bbbk (\mathscr {G}_{0}), \Bbbk (\mathscr {G}_{1})\big )$
correspond to normal subgroupoids
![]() $\big (\mathscr {G}_{0}, \mathscr {G}_{1}\setminus S_{1}\big )$
, as we know from Proposition 4.17.
$\big (\mathscr {G}_{0}, \mathscr {G}_{1}\setminus S_{1}\big )$
, as we know from Proposition 4.17.
In this situation,
![]() ${\mathcal H} /I \cong \Bbbk (\mathscr {G}_{1}\setminus S_{1})$
and we denote
${\mathcal H} /I \cong \Bbbk (\mathscr {G}_{1}\setminus S_{1})$
and we denote
![]() . Now, consider an arbitrary term
. Now, consider an arbitrary term
![]() $\sum _{i=1}^{n}\alpha _{i}f_{g_{i}}$
in
$\sum _{i=1}^{n}\alpha _{i}f_{g_{i}}$
in
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, where n is a positive integer,
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, where n is a positive integer,
![]() $g_{i}\in \mathscr {G}_{1}$
, and
$g_{i}\in \mathscr {G}_{1}$
, and
![]() $\alpha _{g_{i}}\in \Bbbk $
. Since
$\alpha _{g_{i}}\in \Bbbk $
. Since
![]() $ \sum _{i=1}^{n}\alpha _{i}f_{g_{i}}\in {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, we have an equality
$ \sum _{i=1}^{n}\alpha _{i}f_{g_{i}}\in {{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
, we have an equality
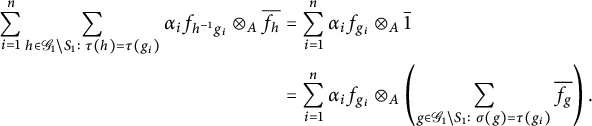 $$ \begin{align*} \sum_{i=1}^{n}\sum_{h\in\mathscr{G}_{1}\setminus S_{1}:\ \tau (h)=\tau (g_{i})}\alpha_{i}f_{h^{-1}g_{i}}\otimes_{A} \overline{f_{h}} & =\sum_{i=1}^{n}\alpha_{i}f_{g_{i}}\otimes_{A} \overline{1} \\ & = \sum_{i=1}^{n}\alpha_{i}f_{g_{i}}\otimes_{A} \left(\sum_{g\in\mathscr{G}_{1}\setminus S_{1}:\ \sigma (g)=\tau (g_{i})}\overline{ f_{g}}\right). \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{n}\sum_{h\in\mathscr{G}_{1}\setminus S_{1}:\ \tau (h)=\tau (g_{i})}\alpha_{i}f_{h^{-1}g_{i}}\otimes_{A} \overline{f_{h}} & =\sum_{i=1}^{n}\alpha_{i}f_{g_{i}}\otimes_{A} \overline{1} \\ & = \sum_{i=1}^{n}\alpha_{i}f_{g_{i}}\otimes_{A} \left(\sum_{g\in\mathscr{G}_{1}\setminus S_{1}:\ \sigma (g)=\tau (g_{i})}\overline{ f_{g}}\right). \end{align*} $$
Noting that
![]() ${\mathcal H}\otimes _{A}\frac {{\mathcal H}}{I} \cong \bigoplus _{(g,h)\in \mathscr {G}_{1} {}_{\tau } \times _{\sigma } \mathscr {N}_{1} } \Bbbk (f_{g}\otimes _{A} \overline {f_{h}})$
as a vector space and that
${\mathcal H}\otimes _{A}\frac {{\mathcal H}}{I} \cong \bigoplus _{(g,h)\in \mathscr {G}_{1} {}_{\tau } \times _{\sigma } \mathscr {N}_{1} } \Bbbk (f_{g}\otimes _{A} \overline {f_{h}})$
as a vector space and that
![]() $h\in \mathscr {G}_{1} \setminus S_{1}\subseteq \mathscr {G}^{(i)}_{1}$
have the same source and target, we obtain a family of equivalent equalities
$h\in \mathscr {G}_{1} \setminus S_{1}\subseteq \mathscr {G}^{(i)}_{1}$
have the same source and target, we obtain a family of equivalent equalities
for any
![]() $h\in \mathscr {G}_{1}\setminus S_{1}$
. Recall the natural action of
$h\in \mathscr {G}_{1}\setminus S_{1}$
. Recall the natural action of
![]() $\mathscr {G}_{1}\setminus S_{1}$
on
$\mathscr {G}_{1}\setminus S_{1}$
on
![]() $\mathscr {G}_{1}$
from (4.1). If we denote the orbits of this action by
$\mathscr {G}_{1}$
from (4.1). If we denote the orbits of this action by
![]() $\mathscr {O}_{1}, \ldots , \mathscr {O}_{m}$
, then the above equalities imply that any arbitrary element in
$\mathscr {O}_{1}, \ldots , \mathscr {O}_{m}$
, then the above equalities imply that any arbitrary element in
![]() $\sum _{i=1}^{n}\alpha _{i}f_{g_{i}}$
in
$\sum _{i=1}^{n}\alpha _{i}f_{g_{i}}$
in
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
can be rewritten as
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
can be rewritten as
![]() $\sum _{j=1}^{m} \alpha _{i_{j}}(\sum _{g\in \mathscr {O}_{j}} f_{g})$
for some subset of indices
$\sum _{j=1}^{m} \alpha _{i_{j}}(\sum _{g\in \mathscr {O}_{j}} f_{g})$
for some subset of indices
![]() $\lbrace i_{j}\rbrace _{j=1}^{m}$
of
$\lbrace i_{j}\rbrace _{j=1}^{m}$
of
![]() $\lbrace i\rbrace _{i=1}^{n}$
.
$\lbrace i\rbrace _{i=1}^{n}$
.
Consequently, any normal Hopf ideal
![]() $I=\Bbbk (S_{1})$
of
$I=\Bbbk (S_{1})$
of
![]() $\big (\Bbbk (\mathscr {G}_{0}), \Bbbk (\mathscr {G}_{1})\big )$
corresponds to the choice of a normal subgroupoid
$\big (\Bbbk (\mathscr {G}_{0}), \Bbbk (\mathscr {G}_{1})\big )$
corresponds to the choice of a normal subgroupoid
![]() and
and
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\cong \Bbbk \big ( ({\mathscr {G}}/{\mathscr {N}})_{1}\big )$
. In particular, since
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}\cong \Bbbk \big ( ({\mathscr {G}}/{\mathscr {N}})_{1}\big )$
. In particular, since
![]() $\Bbbk \big ( ({\mathscr {G}}/{\mathscr {N}})_{1}\big )$
is semisimple, any module (such as
$\Bbbk \big ( ({\mathscr {G}}/{\mathscr {N}})_{1}\big )$
is semisimple, any module (such as
![]() ${\mathcal H}$
) over it is flat and thereby any ring extension over it is faithfully flat, hence pure.
${\mathcal H}$
) over it is flat and thereby any ring extension over it is faithfully flat, hence pure.
Having identified the objects on the left-hand side of the bijection in Theorem 4.26, we observe that the theorem tells us that any Hopf subalgebroid
![]() ${\mathcal K}$
of
${\mathcal K}$
of
![]() ${\mathcal H} = \Bbbk (\mathscr {G}_{1})$
for which
${\mathcal H} = \Bbbk (\mathscr {G}_{1})$
for which
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${\mathcal K}$
is of the form
${\mathcal K}$
is of the form
![]() $\Bbbk \big ( ({\mathscr {G}}/{\mathscr {N}})_{1}\big )$
for some quotient groupoid
$\Bbbk \big ( ({\mathscr {G}}/{\mathscr {N}})_{1}\big )$
for some quotient groupoid
![]() $\mathscr {G} / \mathscr {N}$
. We can observe this directly by looking at the set of characters
$\mathscr {G} / \mathscr {N}$
. We can observe this directly by looking at the set of characters
![]() $\mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
on
$\mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
on
![]() ${\mathcal K}$
. Since
${\mathcal K}$
. Since
![]() $\mathrm {CAlg}_{\Bbbk }({{\mathcal H}},{\Bbbk }) = \mathscr {G}_{1} $
, we have a natural map
$\mathrm {CAlg}_{\Bbbk }({{\mathcal H}},{\Bbbk }) = \mathscr {G}_{1} $
, we have a natural map
![]() $\pi \colon \mathscr {G}_{1}\rightarrow \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk ) $
coming from the inclusion
$\pi \colon \mathscr {G}_{1}\rightarrow \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk ) $
coming from the inclusion
![]() $\iota \colon {\mathcal K}\rightarrow {\mathcal H}$
. Since
$\iota \colon {\mathcal K}\rightarrow {\mathcal H}$
. Since
![]() $\iota $
is pure and since elements from
$\iota $
is pure and since elements from
![]() $\mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
are in bijection with the maximal ideals in
$\mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
are in bijection with the maximal ideals in
![]() ${\mathcal K}$
, Proposition 2.1 entails that
${\mathcal K}$
, Proposition 2.1 entails that
![]() $\pi $
is surjective. Note that
$\pi $
is surjective. Note that
![]() $\mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk ) $
obtains a natural groupoid structure over
$\mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk ) $
obtains a natural groupoid structure over
![]() $\mathscr {G}_{0}=\mathrm {CAlg}_{\Bbbk }(A,\Bbbk ) $
via the structure maps and thereby
$\mathscr {G}_{0}=\mathrm {CAlg}_{\Bbbk }(A,\Bbbk ) $
via the structure maps and thereby
![]() $\pi $
becomes a morphism of groupoids. It is then easy to see that we are in the situation of Lemma 4.5.
$\pi $
becomes a morphism of groupoids. It is then easy to see that we are in the situation of Lemma 4.5.
Proposition 4.28 Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid, and let
$(A, {\mathcal H})$
be a commutative Hopf algebroid, and let
![]() $(A,{\mathcal K})$
be a sub-Hopf algebroid of
$(A,{\mathcal K})$
be a sub-Hopf algebroid of
![]() $(A,{\mathcal H})$
. Denote by
$(A,{\mathcal H})$
. Denote by
![]() $\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. Then the canonical morphism
$\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. Then the canonical morphism
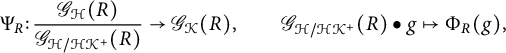 $$ \begin{align} \Psi_R \colon {\displaystyle\frac{\mathscr{G}_{\mathcal H}(R)}{\mathscr{G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+}(R)}} \to \mathscr{G}_{\mathcal K}(R), \qquad \mathscr{G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+}(R)\bullet g \mapsto \Phi_R(g), \end{align} $$
$$ \begin{align} \Psi_R \colon {\displaystyle\frac{\mathscr{G}_{\mathcal H}(R)}{\mathscr{G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+}(R)}} \to \mathscr{G}_{\mathcal K}(R), \qquad \mathscr{G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+}(R)\bullet g \mapsto \Phi_R(g), \end{align} $$
induced by
![]() $\phi $
is injective for every
$\phi $
is injective for every
![]() $R \in \mathrm {CAlg}_{\Bbbk }$
. That is to say, the kernel of the R-component
$R \in \mathrm {CAlg}_{\Bbbk }$
. That is to say, the kernel of the R-component
![]() $\Phi _R \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},R) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},R)$
of the canonical morphism induced by
$\Phi _R \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},R) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},R)$
of the canonical morphism induced by
![]() $\phi $
is
$\phi $
is
![]() $\mathrm {CAlg}_{\Bbbk }({\mathcal H}/{\mathcal H} {\mathcal K}^+,R)$
.
$\mathrm {CAlg}_{\Bbbk }({\mathcal H}/{\mathcal H} {\mathcal K}^+,R)$
.
Proof Recall from [Reference Mackenzie26, Definition 2.6] that the kernel of
![]() $\Phi _R$
is the set
$\Phi _R$
is the set
and that it is a normal subgroupoid of
![]() $\big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
. Now, it is clear that if
$\big (\mathscr {G}_A(R),\mathscr {G}_{\mathcal H}(R)\big )$
. Now, it is clear that if
![]() $h \colon {\mathcal H}/{\mathcal H}{\mathcal K}^+ \to R$
is an algebra morphism, then
$h \colon {\mathcal H}/{\mathcal H}{\mathcal K}^+ \to R$
is an algebra morphism, then
![]() $h \circ \pi \in \ker (\Phi _R)$
: for every
$h \circ \pi \in \ker (\Phi _R)$
: for every
![]() $x \in {\mathcal K}$
, we have
$x \in {\mathcal K}$
, we have
Conversely, if
![]() $f {\kern-1.5pt}\in{\kern-1.5pt} \mathscr {G}_{\mathcal H}(R)$
is such that
$f {\kern-1.5pt}\in{\kern-1.5pt} \mathscr {G}_{\mathcal H}(R)$
is such that
![]() $f {\kern-1.5pt}\circ{\kern-1.5pt} \phi {\kern-1.5pt}={\kern-1.5pt} x {\kern-1.5pt}\circ{\kern-1.5pt} \varepsilon _{\mathcal K}$
, then
$f {\kern-1.5pt}\circ{\kern-1.5pt} \phi {\kern-1.5pt}={\kern-1.5pt} x {\kern-1.5pt}\circ{\kern-1.5pt} \varepsilon _{\mathcal K}$
, then
![]() $f({\mathcal H}{\mathcal K}^+) {\kern-1.5pt}\subseteq{\kern-1.5pt} f({\mathcal H})f({\mathcal K}^+) = 0$
and hence there exists a unique
$f({\mathcal H}{\mathcal K}^+) {\kern-1.5pt}\subseteq{\kern-1.5pt} f({\mathcal H})f({\mathcal K}^+) = 0$
and hence there exists a unique
![]() $h \in \mathrm {CAlg}_{\Bbbk }({\mathcal H}/{\mathcal H}{\mathcal K}^+,R)$
such that
$h \in \mathrm {CAlg}_{\Bbbk }({\mathcal H}/{\mathcal H}{\mathcal K}^+,R)$
such that
![]() $h \circ \pi = f$
.
$h \circ \pi = f$
.
Corollary 4.29 Let
![]() $(A, {\mathcal H})$
be a commutative Hopf algebroid such that
$(A, {\mathcal H})$
be a commutative Hopf algebroid such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat, and let
${}_{s} {{{\mathcal H}}}$
is A-flat, and let
![]() $I\subseteq {\mathcal H}$
be a normal Hopf ideal such that
$I\subseteq {\mathcal H}$
be a normal Hopf ideal such that
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${{{\mathcal H}}{}^{I}}$
. Denote by
${{{\mathcal H}}{}^{I}}$
. Denote by
![]() $\phi \colon {{{\mathcal H}}{}^{I}} \to {\mathcal H}$
the inclusion. Then the canonical morphism
$\phi \colon {{{\mathcal H}}{}^{I}} \to {\mathcal H}$
the inclusion. Then the canonical morphism
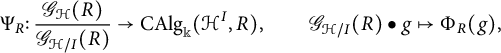 $$ \begin{align*} \Psi_R \colon {\displaystyle\frac{\mathscr{G}_{\mathcal H}(R)}{\mathscr{G}_{{\mathcal H}/I}(R)}} \to \mathrm{CAlg}_{\Bbbk}({{{\mathcal H}}{}^{I}}, R), \qquad \mathscr{G}_{{\mathcal H}/I}(R)\bullet g \mapsto \Phi_R(g), \end{align*} $$
$$ \begin{align*} \Psi_R \colon {\displaystyle\frac{\mathscr{G}_{\mathcal H}(R)}{\mathscr{G}_{{\mathcal H}/I}(R)}} \to \mathrm{CAlg}_{\Bbbk}({{{\mathcal H}}{}^{I}}, R), \qquad \mathscr{G}_{{\mathcal H}/I}(R)\bullet g \mapsto \Phi_R(g), \end{align*} $$
of Lemma 4.22 is injective for every
![]() $R \in \mathrm {CAlg}_{\Bbbk }$
. That is to say, the kernel of the morphism
$R \in \mathrm {CAlg}_{\Bbbk }$
. That is to say, the kernel of the morphism
![]() $\Phi _R \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},R) \to \mathrm {CAlg}_{\Bbbk }({{{\mathcal H}}{}^{I}}, R)$
induced by
$\Phi _R \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},R) \to \mathrm {CAlg}_{\Bbbk }({{{\mathcal H}}{}^{I}}, R)$
induced by
![]() $\phi $
is exactly
$\phi $
is exactly
![]() $\mathrm {CAlg}_{\Bbbk }({\mathcal H}/I,R)$
.
$\mathrm {CAlg}_{\Bbbk }({\mathcal H}/I,R)$
.
Proof It follows from Proposition 4.28 in view of Theorem 4.26, since if
![]() then
then
![]() $I = {\mathcal H}{\mathcal K}^+$
.
$I = {\mathcal H}{\mathcal K}^+$
.
Remark 4.30 Recall the following well-known fact. Suppose that
![]() $(A,{\mathcal K})$
is a sub-Hopf algebroid of a commutative Hopf algebroid
$(A,{\mathcal K})$
is a sub-Hopf algebroid of a commutative Hopf algebroid
![]() $(A,{\mathcal H})$
such that
$(A,{\mathcal H})$
such that
![]() ${\mathcal H}_{\mathcal K}$
is pure (resp. faithfully flat) and denote by
${\mathcal H}_{\mathcal K}$
is pure (resp. faithfully flat) and denote by
![]() $\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. For every commutative
$\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. For every commutative
![]() $\Bbbk $
-algebra R and for every
$\Bbbk $
-algebra R and for every
![]() $g \in \mathscr {G}_{\mathcal K}(R)$
, the pushout diagram
$g \in \mathscr {G}_{\mathcal K}(R)$
, the pushout diagram
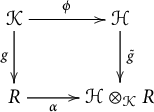
in the category of commutative algebras provides for us a pure (resp. faithfully flat) extension
of R and a point
![]() $\tilde {g} \in \mathscr {G}_{\mathcal H}(S)$
such that
$\tilde {g} \in \mathscr {G}_{\mathcal H}(S)$
such that
![]() $g_S = \Phi _S(\tilde {g})$
, where
$g_S = \Phi _S(\tilde {g})$
, where
is the image of g in
![]() $\mathscr {G}_{\mathcal K}(S)$
. This means that even if the
$\mathscr {G}_{\mathcal K}(S)$
. This means that even if the
![]() $\Psi \colon \mathscr {G}_{\mathcal H}/\mathscr {G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+} \to \mathscr {G}_{\mathcal K}$
whose R-component is retrieved in (4.9) may not be surjective for every R, it is still “locally surjective” in the sense that any element of
$\Psi \colon \mathscr {G}_{\mathcal H}/\mathscr {G}_{{\mathcal H}/{\mathcal H}{\mathcal K}^+} \to \mathscr {G}_{\mathcal K}$
whose R-component is retrieved in (4.9) may not be surjective for every R, it is still “locally surjective” in the sense that any element of
![]() $\mathscr {G}_{\mathcal K}(R)$
arises by patching, in some covering, elements which come from
$\mathscr {G}_{\mathcal K}(R)$
arises by patching, in some covering, elements which come from
![]() $\mathscr {G}_{\mathcal H}$
. This also raises the important question of determining if and when a commutative Hopf algebroid is pure (resp. faithfully flat) over any sub-Hopf algebroid.
$\mathscr {G}_{\mathcal H}$
. This also raises the important question of determining if and when a commutative Hopf algebroid is pure (resp. faithfully flat) over any sub-Hopf algebroid.
Lemma 2.5 can also be used to prove Proposition 4.31, which is the natural extension of [Reference Takeuchi36, Corollary 3.12] to the present setting.
Proposition 4.31 Suppose that
![]() $\Bbbk $
is an algebraically closed field. Let
$\Bbbk $
is an algebraically closed field. Let
![]() $(A,{\mathcal K})$
be a sub-Hopf algebroid of a commutative Hopf algebroid
$(A,{\mathcal K})$
be a sub-Hopf algebroid of a commutative Hopf algebroid
![]() $(A,{\mathcal H})$
such that
$(A,{\mathcal H})$
such that
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${\mathcal K}$
. Denote by
${\mathcal K}$
. Denote by
![]() $\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. Then the
$\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. Then the
![]() $\Bbbk $
-component
$\Bbbk $
-component
![]() $\Phi _{\Bbbk } \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},\Bbbk ) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
of the canonical morphism induced by
$\Phi _{\Bbbk } \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},\Bbbk ) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
of the canonical morphism induced by
![]() $\phi $
is surjective.
$\phi $
is surjective.
Proof If
![]() ${\mathcal H}$
is finitely generated as a
${\mathcal H}$
is finitely generated as a
![]() $\Bbbk $
-algebra, then the statement follows from Hilbert’s Nullstellensatz and Proposition 2.1(7).
$\Bbbk $
-algebra, then the statement follows from Hilbert’s Nullstellensatz and Proposition 2.1(7).
In the general case, let us proceed as follows. Observe that
![]() ${\mathcal H}$
, as an algebra, is the colimit of its subalgebras of the form
${\mathcal H}$
, as an algebra, is the colimit of its subalgebras of the form
![]() ${\mathcal L}{\mathcal K}$
, where
${\mathcal L}{\mathcal K}$
, where
![]() ${\mathcal L}$
is a finitely generated subalgebra.
${\mathcal L}$
is a finitely generated subalgebra.
Now, take
![]() $f \in \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
. Being an algebra map, f allows us to see
$f \in \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
. Being an algebra map, f allows us to see
![]() $\Bbbk $
as a
$\Bbbk $
as a
![]() ${\mathcal K}$
-algebra and we may consider the finitely generated
${\mathcal K}$
-algebra and we may consider the finitely generated
![]() $\Bbbk $
-algebra
$\Bbbk $
-algebra
![]() ${\mathcal L}{\mathcal K} \otimes _{{\mathcal K}} \Bbbk $
.
${\mathcal L}{\mathcal K} \otimes _{{\mathcal K}} \Bbbk $
.
Since the chain of inclusions
![]() ${\mathcal K} \subseteq {\mathcal L}{\mathcal K} \subseteq {\mathcal H}$
is composed by
${\mathcal K} \subseteq {\mathcal L}{\mathcal K} \subseteq {\mathcal H}$
is composed by
![]() ${\mathcal K}$
-ring maps and
${\mathcal K}$
-ring maps and
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${\mathcal K}$
, we may apply Corollary 2.4 to claim that
${\mathcal K}$
, we may apply Corollary 2.4 to claim that
![]() ${\mathcal K} \subseteq {\mathcal L}{\mathcal K}$
is pure and hence the inclusion
${\mathcal K} \subseteq {\mathcal L}{\mathcal K}$
is pure and hence the inclusion
entails that
![]() ${\mathcal L}{\mathcal K} \otimes _{{\mathcal K}} \Bbbk $
is nonzero. By the Nullstellensatz again,
${\mathcal L}{\mathcal K} \otimes _{{\mathcal K}} \Bbbk $
is nonzero. By the Nullstellensatz again,
![]() $\mathrm {CAlg}_{\Bbbk }\left ({\mathcal L}{\mathcal K} \otimes _{{\mathcal K}} \Bbbk ,\Bbbk \right )$
is nonempty, and hence we may take a g therein. The composition
$\mathrm {CAlg}_{\Bbbk }\left ({\mathcal L}{\mathcal K} \otimes _{{\mathcal K}} \Bbbk ,\Bbbk \right )$
is nonempty, and hence we may take a g therein. The composition
satisfies
![]() $g'\left (x\right ) = g\left (x \otimes _{{\mathcal K}} 1 \right ) = g \left (1 \otimes _{{\mathcal K}} f(x)\right ) = f(x)$
for all
$g'\left (x\right ) = g\left (x \otimes _{{\mathcal K}} 1 \right ) = g \left (1 \otimes _{{\mathcal K}} f(x)\right ) = f(x)$
for all
![]() $x \in {\mathcal K}$
, and hence any
$x \in {\mathcal K}$
, and hence any
![]() $f \in \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
can be extended to a
$f \in \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
can be extended to a
![]() $g' \in \mathrm {CAlg}_{\Bbbk }({\mathcal L}{\mathcal K},\Bbbk )$
for every finitely generated subalgebra
$g' \in \mathrm {CAlg}_{\Bbbk }({\mathcal L}{\mathcal K},\Bbbk )$
for every finitely generated subalgebra
![]() ${\mathcal L}$
of
${\mathcal L}$
of
![]() ${\mathcal H}$
. Therefore,
${\mathcal H}$
. Therefore,
![]() $\Phi _{\Bbbk } \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},\Bbbk ) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
is surjective.
$\Phi _{\Bbbk } \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},\Bbbk ) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
is surjective.
Corollary 4.32 Suppose that
![]() $\Bbbk $
is an algebraically closed field. Let I be a normal Hopf ideal of the commutative Hopf algebroid
$\Bbbk $
is an algebraically closed field. Let I be a normal Hopf ideal of the commutative Hopf algebroid
![]() $(A,{\mathcal H})$
such that
$(A,{\mathcal H})$
such that
![]() ${}_{s} {{{\mathcal H}}}$
is A-flat and
${}_{s} {{{\mathcal H}}}$
is A-flat and
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
. Then the
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}}$
. Then the
![]() $\Bbbk $
-component
$\Bbbk $
-component
![]() $\Psi _{\Bbbk }$
of the canonical morphism (4.8) from Lemma 4.22 is an isomorphism. That is to say,
$\Psi _{\Bbbk }$
of the canonical morphism (4.8) from Lemma 4.22 is an isomorphism. That is to say,
Proof Surjectivity follows by Proposition 4.31, in view of the fact that
![]() ${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}} = {{{\mathcal H}}{}^{I}}$
is a sub-Hopf algebroid of
${{\mathcal H}}^{\textsf {co}{\frac {{\mathcal H}}{I}}} = {{{\mathcal H}}{}^{I}}$
is a sub-Hopf algebroid of
![]() ${\mathcal H}$
by Proposition 4.25. Injectivity follows from Corollary 4.29.
${\mathcal H}$
by Proposition 4.25. Injectivity follows from Corollary 4.29.
Corollary 4.33 Suppose that
![]() $\Bbbk $
is an algebraically closed field. Let
$\Bbbk $
is an algebraically closed field. Let
![]() $(A,{\mathcal K})$
be a sub-Hopf algebroid of the commutative Hopf algebroid
$(A,{\mathcal K})$
be a sub-Hopf algebroid of the commutative Hopf algebroid
![]() $(A,{\mathcal H})$
such that
$(A,{\mathcal H})$
such that
![]() ${\mathcal H}$
is pure over
${\mathcal H}$
is pure over
![]() ${\mathcal K}$
. Denote by
${\mathcal K}$
. Denote by
![]() $\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. Then the kernel of the
$\phi \colon {\mathcal K} \to {\mathcal H}$
the inclusion. Then the kernel of the
![]() $\Bbbk $
-component
$\Bbbk $
-component
![]() $\Phi _{\Bbbk } \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},\Bbbk ) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
of the canonical morphism induced by
$\Phi _{\Bbbk } \colon \mathrm {CAlg}_{\Bbbk }({\mathcal H},\Bbbk ) \to \mathrm {CAlg}_{\Bbbk }({\mathcal K},\Bbbk )$
of the canonical morphism induced by
![]() $\phi $
is
$\phi $
is
![]() $\mathrm {CAlg}_{\Bbbk }({\mathcal H}/{\mathcal H} {\mathcal K}^+,\Bbbk )$
. That is to say,
$\mathrm {CAlg}_{\Bbbk }({\mathcal H}/{\mathcal H} {\mathcal K}^+,\Bbbk )$
. That is to say,
Acknowledgment
Laiachi El Kaoutit would like to thank Leovigilio Alonso Tarrío and Ana Jeremías López for helpful discussions. He would also like to thank all the members of the Département de Mathématique, Université Libre de Bruxelles for the excellent ambience during his visit. Aryan Ghobadi would like to thank the University of Granada for their hospitality during his visit.




