Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T13:08:52.529Z Has data issue: false hasContentIssue false
  • English
  • Français

On a certain kind of reducible rational fractions

Published online by Cambridge University Press:  17 April 2009

Mordechai Lewin
Mordechai Lewin
Affiliation:
Department of Mathematics, Israel Institute of Technology, Technion, Haifa, Israel.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The rational fraction

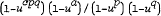
a, c, p, q positive integers, reduces to a polynomial under conditions specified in a result of Grosswald who also stated necessary and sufficient conditions for all the coefficients to tie nonnegative.

This last result is given a different proof using lemmas interesting in themselves.

The method of proof is used in order to give necessary and sufficient conditions for the positive coefficients to be equal to one. For a < 2pq, a = αp + βq, α, β nonnegative integers, c > 1, the exact positions of the nonzero coefficients are established. Also a necessary and sufficient condition for the number of vanishing coefficients to be minimal is given.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 21 , Issue 3 , June 1980 , pp. 321 - 328
Copyright
Copyright © Australian Mathematical Society 1980

References

[1]Brauer, Alfred, “On a problem of partitions”, Amer. J. Math. 64, (1942), 299–312.CrossRefGoogle Scholar
[2]Grosswald, Emil, “Reducible rational fractions of the type of Gaussian polynomials with only non-negative coefficients”, Canad. Math. Bull. 21 (1978), 21–30.CrossRefGoogle Scholar