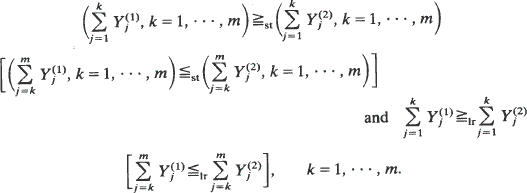Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shaked, Moshe
and
Shanthikumar, J.George
1987.
Temporal stochastic convexity and concavity.
Stochastic Processes and their Applications,
Vol. 27,
Issue. ,
p.
1.
Yao, David D.
and
George Shanthikumar, J.
1988.
Allocating a joint setup in a multi-cell system.
Annals of Operations Research,
Vol. 15,
Issue. 1,
p.
155.
Shaked, Moshe
and
Shanthikumar, J. George
1988.
Stochastic convexity and its applications.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
427.
Shaked, Moshe
and
Shanthikumar, J. George
1988.
Stochastic convexity and its applications.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
427.
Kel'bert, M. Ya.
and
Sukhov, Yu. M.
1990.
Mathematical theory of queuing networks.
Journal of Soviet Mathematics,
Vol. 50,
Issue. 3,
p.
1527.
Kouvelis, Panagiotis
and
Tirupati, Devanath
1991.
Approximate performance modeling and decision making for manufacturing systems: A queueing network optimization framework.
Journal of Intelligent Manufacturing,
Vol. 2,
Issue. 2,
p.
107.
Lee, Heungsoon Felix
Srinivasan, Mandyam M.
and
Yano, Candace A.
1991.
Characteristics of optimal workload allocation for closed queueing networks.
Performance Evaluation,
Vol. 12,
Issue. 4,
p.
255.
Chang, Cheng-Shang
1992.
A new ordering for stochastic majorization: theory and applications.
Advances in Applied Probability,
Vol. 24,
Issue. 3,
p.
604.
Chang, Cheng-Shang
1992.
A new ordering for stochastic majorization: theory and applications.
Advances in Applied Probability,
Vol. 24,
Issue. 3,
p.
604.
Bitran, Gabriel R.
and
Dasu, Sriram
1992.
A review of open queueing network models of manufacturing systems.
Queueing Systems,
Vol. 12,
Issue. 1-2,
p.
95.
Buzacott, John A.
and
Shanthikumar, J. George
1992.
Design of manufacturing systems using queueing models.
Queueing Systems,
Vol. 12,
Issue. 1-2,
p.
135.
Li, Haijun
and
Shaked, Moshe
1993.
Stochastic majorization of stochastically monotone families of random variables.
Advances in Applied Probability,
Vol. 25,
Issue. 4,
p.
895.
Li, Haijun
and
Shaked, Moshe
1993.
Stochastic majorization of stochastically monotone families of random variables.
Advances in Applied Probability,
Vol. 25,
Issue. 4,
p.
895.
Sparaggis, P. D.
Towsley, D.
and
Cassandras, C. G.
1993.
Extremal properties of the shortest/longest non-full queue policies in finite-capacity systems with state-dependent service rates.
Journal of Applied Probability,
Vol. 30,
Issue. 1,
p.
223.
Sparaggis, P. D.
Towsley, D.
and
Cassandras, C. G.
1993.
Extremal properties of the shortest/longest non-full queue policies in finite-capacity systems with state-dependent service rates.
Journal of Applied Probability,
Vol. 30,
Issue. 01,
p.
223.
Chang, Cheng-Shang
Shanthikumar, J. George
and
Yao, David D.
1994.
Stochastic Modeling and Analysis of Manufacturing Systems.
p.
189.
Li, Haijun
1994.
On a Class of Stochastic Arrangement Inequalities Arising in Optimal Allocation of Resources.
Probability in the Engineering and Informational Sciences,
Vol. 8,
Issue. 1,
p.
113.
Buzacott, John A.
Shanthikumar, J. George
and
Yao, David D.
1994.
Stochastic Modeling and Analysis of Manufacturing Systems.
p.
1.
Nicol, D.M.
Simha, R.
and
Towsley, D.
1996.
Static assignment of stochastic tasks using majorization.
IEEE Transactions on Computers,
Vol. 45,
Issue. 6,
p.
730.
Lewis, Gordon H.
Srinivasan, Ashok
and
Subrahmanian, Eswaran
1998.
Staffing and Allocation of Workers in an Administrative Office.
Management Science,
Vol. 44,
Issue. 4,
p.
548.
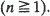 Let
Let 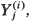 (j = 1, …, m; i = 1,2) be 2m independent random variables that have proportional equilibrium rates with
(j = 1, …, m; i = 1,2) be 2m independent random variables that have proportional equilibrium rates with 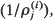 (j = 1, …, m; i = 1, 2) as the constant of proportionality. When the equilibrium rate is increasing and concave [convex] it is shown that
(j = 1, …, m; i = 1, 2) as the constant of proportionality. When the equilibrium rate is increasing and concave [convex] it is shown that 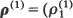 , …,
, …, 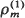 ) majorizes
) majorizes 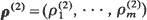 implies
implies 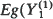 , …,
, …, 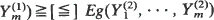 for all increasing Schur-convex [concave] functions
for all increasing Schur-convex [concave] functions 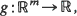 whenever the expectations exist. In addition if
whenever the expectations exist. In addition if 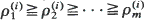 , (i = 1, 2), then
, (i = 1, 2), then