Hostname: page-component-7bb8b95d7b-s9k8s Total loading time: 0 Render date: 2024-09-19T09:35:02.798Z Has data issue: false hasContentIssue false
  • English
  • Français

On parametric density estimators

Published online by Cambridge University Press:  01 July 2016

C. R. Heathcote
C. R. Heathcote*
Affiliation:
The Australian National University, Canberra
Get access Rights & Permissions [Opens in a new window]

Extract

There is an extensive literature on estimating a probability density (or some other appropriate curve) f using statistics of the form 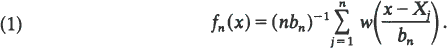Here X1, X2, · · ·, Xn is a sample from the population, the weight function w is constrained by suitable regularity conditions, and the sequence {bn} of band-widths satisfies bn → 0, nbn → ∞ as n → ∞. Rosenblatt (1971) presents details of this method of estimation and provides an extensive list of references.

Type
Research Article
Information
Advances in Applied Probability , Volume 10 , Issue 4 , December 1978 , pp. 735 - 740
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. F., Bickel, P. J., Hampel, F. R., Huber, P. J., Rogers, W. H. and Tukey, J. W. (1972) Robust Estimates of Location. Princeton University Press.Google Scholar
Beran, R. (1977) Minimum Hellinger distance estimates for parametric models. Ann. Statist. 3, 445–463.Google Scholar
Heathcote, C. R. (1977) The integrated squared error estimation of parameters. Biometrika 64, 255–264.Google Scholar
Huber, P. J. (1972) Robust statistics; a review. Ann. Math. Statist. 43, 1041–1067.CrossRefGoogle Scholar
Pickands, J. (1969) Efficient estimation of a probability density function. Ann. Math. Statist. 40, 854–864.Google Scholar
Rosenblatt, M. (1971) Curve estimates. Ann. Math. Statist. 42, 1815–1842.Google Scholar