Research Article
Weight ω in stable theories with few types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 353-373
-
- Article
- Export citation
Martin's axiom and the continuum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 374-391
-
- Article
- Export citation
The dimension of the negation of transitive closure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 392-414
-
- Article
- Export citation
Ultrafilters generated by a closed set of functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 415-430
-
- Article
- Export citation
On the equivalence of certain consequences of the proper forcing axiom
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 431-443
-
- Article
- Export citation
Hechler reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 444-458
-
- Article
- Export citation
On the basic logic of STIT with a single agent
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 459-483
-
- Article
- Export citation
Anneaux de fonctions p-adiques
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 484-497
-
- Article
- Export citation
The decidability of dependency in intuitionistic propositional logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 498-504
-
- Article
- Export citation
The thickness lemma from P− + IΣ1 + ¬BΣ2
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 505-511
-
- Article
- Export citation
The isomorphism property for nonstandard universes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 512-516
-
- Article
- Export citation
Complete problems for fixed-point logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 517-527
-
- Article
- Export citation
Corps et chirurgie
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 528-533
-
- Article
- Export citation
Possible behaviours of the reflection ordering of stationary sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 534-547
-
- Article
- Export citation
Élimination des quantificateurs dans des paires de corps
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 548-562
-
- Article
- Export citation
A geometric proof of the completeness of the Łukasiewicz calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 563-578
-
- Article
- Export citation
A star-free semantics for R
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 579-590
-
- Article
- Export citation
Cylindric modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 591-623
-
- Article
- Export citation
Ultrafilters on ω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 624-639
-
- Article
- Export citation
Models of intuitionistic TT and NF
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 640-653
-
- Article
- Export citation

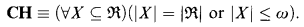
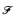 a filter on
a filter on 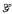 a set of functions from
a set of functions from 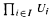 such that, for all
such that, for all 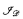 on the set of functions
on the set of functions 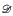 on
on 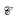 (
(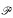 by a prime ideal
by a prime ideal 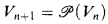 for
for 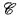 of
of 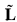
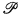
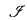
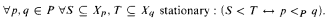
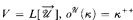 , and
, and 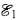 et
et 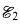 donnés, il existe des points du sous-corps rationnels pour
donnés, il existe des points du sous-corps rationnels pour