Article contents
Complete problems for fixed-point logics
Published online by Cambridge University Press: 12 March 2014
Extract
The notion of logical reducibilities is derived from the idea of interpretations between theories. It was used by Lovász and Gács [LG77] and Immerman [Imm87] to give complete problems for certain complexity classes and hence establish new connections between logical definability and computational complexity.
However, the notion is also interesting in a purely logical context. For example, it is helpful to establish nonexpressibility results.
We say that a class 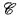 of τ-structures is a >complete problem for a logic
of τ-structures is a >complete problem for a logic 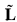 under L-reductions if it is definable in
under L-reductions if it is definable in 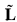 [τ] and if every class definable in
[τ] and if every class definable in 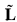 can be ”translated” into
can be ”translated” into 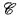 by L-formulae (cf. §4).
by L-formulae (cf. §4).
We prove the following theorem:
1.1. Theorem. There are complete problems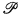 for partial fixed-point logic and
for partial fixed-point logic and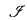 for inductive fixed-point logic under quantifier-free reductions.
for inductive fixed-point logic under quantifier-free reductions.
The main step of the proof is to establish a new normal form for fixed-point formulae (which might be of some interest itself). To obtain this normal form we use theorems of Abiteboul and Vianu [AV91a] that show the equivalence between the fixed-point logics we consider and certain extensions of the database query language Datalog.
In [Dah87] Dahlhaus gave a complete problem for least fixed-point logic. Since least fixed-point logic equals inductive fixed-point logic by a well-known result of Gurevich and Shelah [GS86], this already proves one part of our theorem.
However, our class 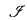 gives a natural description of the fixed-point process of an inductive fixed-point formula and hence sheds some light on completely different aspects of the logic than Dahlhaus's construction, which is strongly based on the features of least fixed-point formulae.
gives a natural description of the fixed-point process of an inductive fixed-point formula and hence sheds some light on completely different aspects of the logic than Dahlhaus's construction, which is strongly based on the features of least fixed-point formulae.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 6
- Cited by




