Let κ and λ be infinite cardinals, 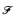a filter on κ and 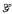a set of functions from κ to κ. The filter 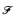is generated by 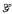if 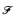consists of those subsets of κ which contain the range of some element of 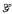. The set 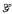is <λ-closed if it is closed in the <λ-topology on κκ. (In general, the <λ-topology on IA has basic open sets all 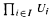such that, for all i ∈ I, Ui ⊆ A and ∣{i ∈ I: Ui ≠ A} ∣<λ.) The primary question considered in this paper asks “Is there a uniform ultrafilter on κ which is generated by a closed set of functions?” (Closed means <ω-closed.) We also establish the independence of two related questions. One is due to Carlson: “Does there exist a regular cardinal κ and a subtree T of <κκ such that the set of branches of T generates a uniform ultrafilter on κ?”; and the other is due to Pouzet: “For all regular cardinals κ, is it true that no uniform ultrafilter on κ is it true that no uniform ultrafilter on κ analytic?”

We show that if κ is a singular, strong limit cardinal, then there is a uniform ultrafilter on κ which is generated by a closed set of increasing functions. Also, from the consistency of an almost huge cardinal, we get the consistency of CH + “There is a uniform ultrafilter on ℵ1 which is generated by a closed set of increasing functions”. In contrast with the above results, we show that if Κ is any cardinal, λ is a regular cardinal less than or equal to κ and ℙ is the forcing notion for adding at least (κ<λ)+ generic subsets of λ, then in VP, no uniform ultrafilter on κ is generated by a closed set of functions.