Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T10:26:12.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Hechler reals

Published online by Cambridge University Press:  12 March 2014

Grzegorz Łabędzki  and
Miroslav Repický
Grzegorz Łabędzki
Affiliation:
Institute of Mathematics, Wrocław University, 50-156 Wrocław, Poland, E-mail: labedz@math.uni.wroc.pl
Miroslav Repický
Affiliation:
Mathematical Institute of the Slovak Academy of Sciences, 041 54 Košice, Slovakia, E-mail: repicky@kosice.upjs.sk
Get access Rights & Permissions [Opens in a new window]

Abstract

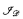We define a σ-ideal on the set of functions ωω with the property that a real x ∈ ωω is a Hechler real over V if and only if x omits all Borel sets in 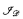. In fact we define a topology 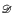on ωω related to Hechler forcing such that 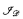is the family of first category sets in 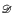. We study cardinal invariants of the ideal .

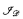Keywords

Hechler realdominating topologymeager setscardinal invariants
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 2 , June 1995 , pp. 444 - 458
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Balcar, B., Pelant, J. and Simon, P., The space of ultrafilters on N covered by nowhere dense sets, Fundamenta Mathematicae, vol. 110 (1980), pp. 11–24.CrossRefGoogle Scholar
[2] Baumgartner, J. E. and Dordal, P., Adjoining dominating functions, this Journal, vol. 50 (1985), no. 1, pp. 94–101.Google Scholar
[3] Brendle, J., Judah, H. and Shelah, S., Combinatorial properties of Hechler forcing, Annals of Pure and Applied Logic, vol. 59 (1992), pp. 185–199.CrossRefGoogle Scholar
[4] Comfort, W. and Negrepontis, S., Theory of ultrafilters, Springer-Verlag, Berlin, 1974.CrossRefGoogle Scholar
[5] Van Douwen, E. K., The integers and topology, The handbook of set-theoretic topology (Kunen, K. and Vaughan, J., editors), North-Holland, Amsterdam, 1984, pp. 111–167.CrossRefGoogle Scholar
[6] Fremlin, D. H., Cichoń's diagram, Publications Mathématiques de l'Université Pierre et Marie Curie, vol. 66, 23eme année, 1983/1984, No. 5 (1984), 13pp.Google Scholar
[7] Fremlin, D. H., Consequences of Martin's axiom, Cambridge University Press, Cambridge, 1984.CrossRefGoogle Scholar
[8] Haworth, R. C. and McCoy, R. A., Baire spaces, Dissertationes Mathematicae/Rozprawy Matematyczne, vol. 141 (1977).Google Scholar
[9] Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[10] Judah, H. and Repický, M., Amoeba reals, preprint.Google Scholar
[11] Miller, A. W., Some properties of measure and category, Transactions of the American Mathematical Society, vol. 266 (1981), pp. 93–114.CrossRefGoogle Scholar
[12] Truss, J., Sets having caliber ℵ1, Logic Colloquium ’76, North-Holland, Amsterdam, 1977, pp. 595–612.Google Scholar