Article contents
Martin's axiom and the continuum
Published online by Cambridge University Press: 12 March 2014
Extract
Since Georg Cantor discovered set theory the main problem in this area of mathematical research has been to discover what is the size of the continuum. The continuum hypothesis (CH) says that every infinite set of reals either has the same cardinality as the set of all reals or has the cardinality of the set of natural numbers, namely
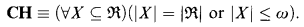
In 1939 Kurt Gödel discovered the Constructible Universe and proved that CH holds in it. In the early sixties Paul Cohen proved that every universe of set theory can be extended to a bigger universe of set theory where CH fails. Moreover, given any reasonable cardinal κ, it is possible to build a model where the continuum size is κ. The new technique discovered by Cohen is called forcing and is being used successfully in other branches of mathematics (analysis, algebra, graph theory, etc.).
In the light of these two stupendous works the experts (especially the platonists) were forced to conclude that from the point of view of the classical axiomatization of set theory (called ZFC) it is impossible to give any answer to the continuum size problem: everything is possible!
In private communications Gödel suggested that the continuum size from a platonistic point of view should be ω2, the second uncountable cardinal. As this is not provable in ZFC, Gödel suggested that a new axiom should be added to ZFC to decide that the cardinality of the continuum is ω2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 1
- Cited by




