Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-07T00:10:23.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Anneaux de fonctions p-adiques

Published online by Cambridge University Press:  12 March 2014

Luc Bélair
Luc Bélair*
Affiliation:
Département de Mathématiques, Université du Québec à Montréal, Montréal, Québec H3C 3P8, Canada, E-mail: belair@math.uqam.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We study first-order properties of the quotient rings 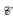(V)/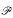 by a prime ideal 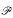where 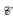(V) is the ring of p-adic valued continuous definable functions on some affine p-adic variety V. We show that they are integrally closed Henselian local rings, with a p-adically closed residue field and field of fractions, and they are not valuation rings in general but always satisfy ∀ x, y(x∣y2 ∨ y∣x2).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 2 , June 1995 , pp. 484 - 497
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

RÉFÉRENCES

[Am] Amice, Y., Les nombres p-adiques, Presses Universitaires de France, Paris, 1975.Google Scholar
[B1] Bélair, L., Anneaux p-adiquement clos et anneaux de fonctions définissables, this Journal, vol. 56 (1991), pp. 539–553.Google Scholar
[B2] Bélair, L., Substructures and uniform elimination for padic fields, Annals of Pure and Applied Logic, vol. 39 (1988), pp. 1–17.CrossRefGoogle Scholar
[BCR] Bochnak, J., Coste, M., et Roy, M.-F., Géométrie algébrique réelle, Springer-Verlag, Berlin, 1987.Google Scholar
[BS] Bröcker, L. et Schinke, J. H., On the L-adic spectrum, Schrittenreihe des Mathematischen Instituts des Universität Münster, ser. 2, vol. 40, Mathematisches Institut Universität Münster, Münster, 1986.Google Scholar
[BR] Brumfiel, G. W., Partially ordered rings and semi-algebraic geometry, Cambridge University Press, Cambridge, 1979.CrossRefGoogle Scholar
[CC] Carral, M. et Coste, M., Normal spectral spaces and their dimension, Jounal of Pure and Applied Algebra, vol. 30 (1983), pp. 227–235.CrossRefGoogle Scholar
[CD] Cherlin, G. et Dickmann, M., Real closed rings, II, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 213–231.CrossRefGoogle Scholar
[CR] Coste, M. et Roy, M.-F., La topologie du spectre réel, Ordered fields and real algebraic geometry, Comtemporary Mathematics, vol. 8, American Mathematical Society, Providence, Rhode Island, 1982, pp. 27–59.CrossRefGoogle Scholar
[De1] Denef, J., The rationality of the Poincaré series associated to the p-adic points on a variety, Inventiones Mathematicae, vol. 77 (1984), pp. 1–23.CrossRefGoogle Scholar
[De2] Denef, J., p-adic semi-algebraic sets and cell decomposition, Jounal für Reine und Angewandte Mathematik, vol. 369 (1986), pp. 154–166.Google Scholar
[D1] Dickmann, M., A property of the continuous semialgebraic functions defined on a real curve, manuscrit.Google Scholar
[D2] Dickmann, M., Applications of model theory to real algebraic geometry: a survey, Methods in Mathematical logic, Proceedings, Caracas, 1983 (Di Prisco, C. A., editor), Lecture Notes in Mathematics, vol. 1130, Springer-Verlag, Berlin, 1985, pp. 76–150.Google Scholar
[D3] Dickmann, M., Applications of model theory to real algebraic geometry (à paraître).Google Scholar
[GJ] Gilman, L. et Jerison, M., Rings of continuous functions, Van Nostrand, Princeton, New Jersey, 1960.CrossRefGoogle Scholar
[Ha] Haskell, D., Topics in constructive p-adic algebra, Ph.D. thesis, Stanford University, Stanford, California, 1990.Google Scholar
[Pi] Pillay, A., Sheaves of continuous definable functions, this Journal, vol. 53 (1988), pp. 1165–1169.Google Scholar
[Sc] Schwartz, N., Real closed rings, Algebra and order: proceedings of the first international symposium on ordered algebraic structures, Luminy-Marseille, 1984 (Wolfenstein, S., editor), Helderman-Verlag, Berlin, 1986, pp. 175–194.Google Scholar
[SV] Scowcroft, P. et Van den Dries, L., On the structure of semialgebraic set over p-adic fields, this Journal, vol. 53 (1988), pp. 1138–1164.Google Scholar
[VD] Van den Dries, L., Dimension of definable sets, algebraic boundedness and Henselian fields, Annals of Pure and Applied Logic, vol. 45 (1989), pp. 189–209.CrossRefGoogle Scholar