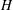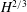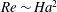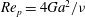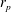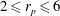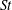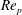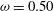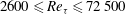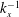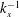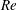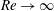Papers
Destabilization of a stratified shear layer by ambient turbulence
-
- Published online by Cambridge University Press:
- 14 April 2015, pp. 1-15
-
- Article
- Export citation
The lift on an aerofoil in grid-generated turbulence
-
- Published online by Cambridge University Press:
- 14 April 2015, pp. 16-35
-
- Article
- Export citation
Internally heated convection beneath a poor conductor
-
- Published online by Cambridge University Press:
- 14 April 2015, pp. 36-56
-
- Article
- Export citation
Thermal effect on large-aspect-ratio Couette–Taylor system: numerical simulations
-
- Published online by Cambridge University Press:
- 14 April 2015, pp. 57-78
-
- Article
- Export citation
Tayler instability in liquid metal columns and liquid metal batteries
-
- Published online by Cambridge University Press:
- 15 April 2015, pp. 79-114
-
- Article
- Export citation
The dynamical states of a prolate spheroidal particle suspended in shear flow as a consequence of particle and fluid inertia
-
- Published online by Cambridge University Press:
- 17 April 2015, pp. 115-158
-
- Article
- Export citation
Generation of nonlinear Marangoni waves in a two-layer film by heating modulation
-
- Published online by Cambridge University Press:
- 17 April 2015, pp. 159-192
-
- Article
- Export citation
Latitudinal libration driven flows in triaxial ellipsoids
-
- Published online by Cambridge University Press:
- 17 April 2015, pp. 193-228
-
- Article
- Export citation
Effects of base flow modifications on noise amplifications: flow past a backward-facing step
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 229-263
-
- Article
- Export citation
Heat transfer mechanisms of a vapour bubble growing at a wall in saturated upward flow
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 264-302
-
- Article
- Export citation
Spectral scaling in boundary layers and pipes at very high Reynolds numbers
-
- Published online by Cambridge University Press:
- 21 April 2015, pp. 303-326
-
- Article
- Export citation
Detachment of droplets from cylinders in flow using an experimental analogue
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 327-340
-
- Article
- Export citation
Vortex separation and interaction in the wake of inclined trapezoidal plates
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 341-369
-
- Article
- Export citation
Modelling intrusions through quiescent and moving ambients
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 370-406
-
- Article
- Export citation
Sources and fluxes of scale energy in the overlap layer of wall turbulence
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 407-423
-
- Article
- Export citation
Cavitation nuclei in water exposed to transient pressures
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 424-448
-
- Article
- Export citation
Stability of the tank treading modes of erythrocytes and its dependence on cytoskeleton reference states
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 449-467
-
- Article
- Export citation
Symmetry-plane model of 3D Euler flows and mapping to regular systems to improve blowup assessment using numerical and analytical solutions
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 468-502
-
- Article
- Export citation
Initial surface deformations during impact on a liquid pool
-
- Published online by Cambridge University Press:
- 20 April 2015, pp. 503-519
-
- Article
- Export citation
A numerical evaluation of the asymptotic theory of receptivity for subsonic compressible boundary layers
-
- Published online by Cambridge University Press:
- 21 April 2015, pp. 520-546
-
- Article
- Export citation