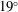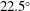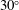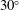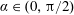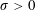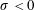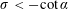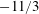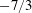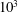JFM Papers
Experimental study of the mean structure and quasi-conical scaling of a swept-compression-ramp interaction at Mach 2
-
- Published online by Cambridge University Press:
- 19 February 2018, pp. 1-27
-
- Article
- Export citation
Dynamics of laser-induced cavitation bubbles near two perpendicular rigid walls
-
- Published online by Cambridge University Press:
- 19 February 2018, pp. 28-49
-
- Article
- Export citation
Spectral broadening of acoustic waves by convected vortices
-
- Published online by Cambridge University Press:
- 19 February 2018, pp. 50-80
-
- Article
- Export citation
On the origin of spanwise vortex deformations in laminar separation bubbles
-
- Published online by Cambridge University Press:
- 19 February 2018, pp. 81-108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The initial development of a jet caused by fluid, body and free surface interaction with a uniformly accelerated advancing or retreating plate. Part 1. The principal flow
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 109-145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The initial development of a jet caused by fluid, body and free surface interaction with a uniformly accelerated advancing or retreating plate. Part 2. Well-posedness and stability of the principal flow
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 146-166
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio–temporal analysis of hydrodynamic forces on the particle bed in an oscillatory flow environment
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 167-202
-
- Article
- Export citation
On the bulk motion of the cerebrospinal fluid in the spinal canal
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 203-227
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Path oscillations and enhanced drag of light rising spheres
-
- Published online by Cambridge University Press:
- 21 February 2018, pp. 228-266
-
- Article
- Export citation
Flow rate–pressure drop relation for deformable shallow microfluidic channels
-
- Published online by Cambridge University Press:
- 21 February 2018, pp. 267-286
-
- Article
- Export citation
Ice breaking by a collapsing bubble
-
- Published online by Cambridge University Press:
- 23 February 2018, pp. 287-309
-
- Article
- Export citation
The effect of ions on the motion of an oil slug through a charged capillary
-
- Published online by Cambridge University Press:
- 21 February 2018, pp. 310-350
-
- Article
- Export citation
Mean turbulence statistics in boundary layers over high-porosity foams
-
- Published online by Cambridge University Press:
- 21 February 2018, pp. 351-379
-
- Article
- Export citation
Instabilities and small-scale waves within the Stewartson layers of a thermally driven rotating annulus
-
- Published online by Cambridge University Press:
- 21 February 2018, pp. 380-407
-
- Article
- Export citation
Drop deformation and emulsion rheology under the combined influence of uniform electric field and linear flow
-
- Published online by Cambridge University Press:
- 23 February 2018, pp. 408-433
-
- Article
- Export citation
Condensates in rotating turbulent flows
-
- Published online by Cambridge University Press:
- 23 February 2018, pp. 434-462
-
- Article
- Export citation
On a unified breaking onset threshold for gravity waves in deep and intermediate depth water
-
- Published online by Cambridge University Press:
- 23 February 2018, pp. 463-488
-
- Article
- Export citation
Large-deformation electrohydrodynamics of an elastic capsule in a DC electric field
-
- Published online by Cambridge University Press:
- 23 February 2018, pp. 489-520
-
- Article
- Export citation
Closure model for homogeneous isotropic turbulence in the Lagrangian specification of the flow field
-
- Published online by Cambridge University Press:
- 23 February 2018, pp. 521-551
-
- Article
- Export citation
Effects of surface roughness on a separating turbulent boundary layer
-
- Published online by Cambridge University Press:
- 26 February 2018, pp. 552-580
-
- Article
- Export citation