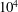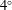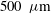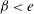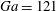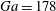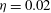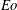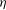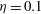Focus on Fluids
Suspension dynamics: moving beyond steady
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Phase dynamics of freely swimming foils
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 5-21
-
- Article
- Export citation
Self-propelled jumping upon drop coalescence on Leidenfrost surfaces
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 22-38
-
- Article
- Export citation
Numerical simulations of self-propelled jumping upon drop coalescence on non-wetting surfaces
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 39-65
-
- Article
- Export citation
Dynamics of liquid films on vertical fibres in a radial electric field
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 66-89
-
- Article
- Export citation
Global stability analysis of flow through a fusiform aneurysm: steady flows
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 90-106
-
- Article
- Export citation
Time-dependent Taylor–Aris dispersion of an initial point concentration
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 107-122
-
- Article
- Export citation
Explosions at the water surface
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 123-139
-
- Article
- Export citation
A universal scaling for low-order structure functions in the log-law region of smooth- and rough-wall boundary layers
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 140-156
-
- Article
- Export citation
Three-dimensional Navier–Stokes simulations of buoyant, vertical miscible Hele-Shaw displacements
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 157-183
-
- Article
- Export citation
Self-destabilizing loop observed in a jetting-to-dripping transition
-
- Published online by Cambridge University Press:
- 02 July 2014, pp. 184-218
-
- Article
- Export citation
On linear instability mechanisms in incompressible open cavity flow
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 219-236
-
- Article
- Export citation
Global modes, receptivity, and sensitivity analysis of diffusion flames coupled with duct acoustics
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 237-265
-
- Article
- Export citation
Ellipsoidal drop impact on a solid surface for rebound suppression
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 266-281
-
- Article
- Export citation
Intrusion-generated waves in a linearly stratified fluid
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 282-295
-
- Article
- Export citation
Experimental control of natural perturbations in channel flow
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 296-309
-
- Article
- Export citation
Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 310-348
-
- Article
- Export citation
Transitional shock-wave/boundary-layer interactions in hypersonic flow
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 349-382
-
- Article
- Export citation
Influence of the viscosity ratio on drop dynamics and breakup for a drop rising in an immiscible low-viscosity liquid
-
- Published online by Cambridge University Press:
- 04 July 2014, pp. 383-409
-
- Article
- Export citation
Ejecta evolution during cone impact
-
- Published online by Cambridge University Press:
- 07 July 2014, pp. 410-438
-
- Article
- Export citation