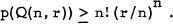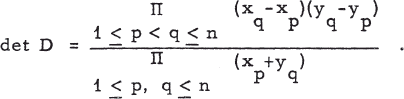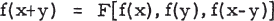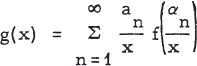Research Article
On a Combinatorial Problem of Erdös and Hajnal
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 177-181
-
- Article
-
- You have access
- Export citation
An Informal Arithmetical Approach to Computability and Computation, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 183-200
-
- Article
-
- You have access
- Export citation
Some Remarks on the Mathieu Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 201-212
-
- Article
-
- You have access
- Export citation
Generating Reflections For U(2, p2n). II, p = 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 213-217
-
- Article
-
- You have access
- Export citation
Partitions of the Natural Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 219-236
-
- Article
-
- You have access
- Export citation
A Module is Flat if and Only if its Character Module is Injective
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 237-243
-
- Article
-
- You have access
- Export citation
The Categories of Boolean Lattices, Boolean Rings and Boolean Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 245-252
-
- Article
-
- You have access
- Export citation
Permanents of (0, 1)-Circulants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 253-263
-
- Article
-
- You have access
- Export citation
Monotony of the Osculating Circles of Arcs of Cyclic Order Three
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-271
-
- Article
-
- You have access
- Export citation
A Generalization of Cauchy' s Double Alternant
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 273-278
-
- Article
-
- You have access
- Export citation
The Solutions of Some Functional Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 279-282
-
- Article
-
- You have access
- Export citation
Finite Reciprocities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-290
-
- Article
-
- You have access
- Export citation
A Remark on the Theorems of Lusin and Egoroff
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 291-295
-
- Article
-
- You have access
- Export citation
Some Useful Matrix Lemmas in Statistical Estimation Theory*
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-300
-
- Article
-
- You have access
- Export citation
On Abel's Binomial Identity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-303
-
- Article
-
- You have access
- Export citation
Book Reviews: Comptes Rendus Critiques
Décomposition des lois de Probabilités, par Y.V. Linnik. Gauthier Villars, Paris 1962. vi + 294 pages. 55 F.
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 325-326
-
- Article
-
- You have access
- Export citation
Ordinary Differential Equations, by Garrett Birkhoff and Gian-Carlo Roba. Ginn and Co., Boston, 1962. viii + 318 pages. $8. 50. - Differential Equations, by H. S. Bear. Addison-Wesley, Reading, Mass., 1962. viii + 207 pages. $7.50.
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 314-315
-
- Article
-
- You have access
- Export citation
News
News from the Departments
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 339-342
-
- Article
-
- You have access
- Export citation
Book Reviews: Comptes Rendus Critiques
Statistical and Inductive Probabilities, by Hugues Leblanc. Prentice-Hall, Inc., 1962. xii + 148 pages.
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 331-332
-
- Article
-
- You have access
- Export citation
Other
Abstracts of Theses
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 343-344
-
- Article
-
- You have access
- Export citation



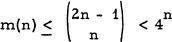
 in the
unitary plane over GF(2
in the
unitary plane over GF(2
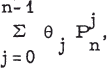 , where θ
, where θ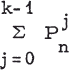 . It has
been conjectured that
. It has
been conjectured that