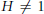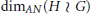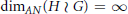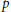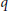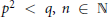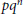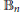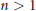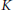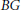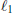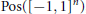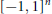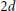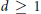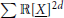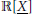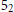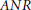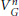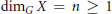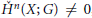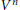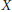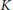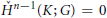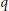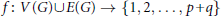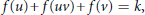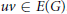Research Article
Small Flag Complexes with Torsion
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-230
-
- Article
-
- You have access
- Export citation
On the Multiplicities of Characters in Table Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 231-239
-
- Article
-
- You have access
- Export citation
Addendum
Addendum to “Limit Sets of Typical Homeomorphisms”
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 240-244
-
- Article
-
- You have access
- Export citation
Research Article
Assouad–Nagata Dimension of Wreath Products of Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 245-253
-
- Article
-
- You have access
- Export citation
On Parseval Wavelet Frames with Two or Three Generators via the Unitary Extension Principle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 254-263
-
- Article
-
- You have access
- Export citation
On Semisimple Hopf Algebras of Dimension pqn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 264-269
-
- Article
-
- You have access
- Export citation
Derivations on Toeplitz Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-276
-
- Article
-
- You have access
- Export citation
On Mutually m-permutable Products of Smooth Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-282
-
- Article
-
- You have access
- Export citation
Infinite Dimensional DeWitt Supergroups and their Bodies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-288
-
- Article
-
- You have access
- Export citation
Closure of the Cone of Sums of 2d-powers in Certain Weighted ℓ1-seminorm Topologies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 289-302
-
- Article
-
- You have access
- Export citation
Award Winners
Octonion Algebras over Rings Are Not Determined by their Norms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-309
-
- Article
-
- You have access
- Export citation
Research Article
Left-orderable Fundamental Group and Dehn Surgery on the Knot 52
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-317
-
- Article
-
- You have access
- Export citation
Duality of Preenvelopes and Pure Injective Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 318-325
-
- Article
-
- You have access
- Export citation
On Zero-divisors in Group Rings of Groups with Torsion
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 326-334
-
- Article
-
- You have access
- Export citation
Alexandroff Manifolds and Homogeneous Continua
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 335-343
-
- Article
-
- You have access
- Export citation
On Localized Unstable K1-groups and Applications to Self-homotopy Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-356
-
- Article
-
- You have access
- Export citation
Representation Equivalent Bieberbach Groups and Strongly Isospectral Flat Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 357-363
-
- Article
-
- You have access
- Export citation
How Lipschitz Functions Characterize the Underlying Metric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 364-374
-
- Article
-
- You have access
- Export citation
A Problem on Edge-magic Labelings of Cycles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 375-380
-
- Article
-
- You have access
- Export citation
On Complex Explicit Formulae Connected with the Möbius Function of an Elliptic Curve
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-389
-
- Article
-
- You have access
- Export citation