Article contents
Closure of the Cone of Sums of 2d-powers in Certain Weighted ℓ1-seminorm Topologies
Published online by Cambridge University Press: 20 November 2018
Abstract
In a paper from 1976, Berg, Christensen, and Ressel prove that the closure of the cone of sums of squares 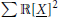 $\sum{\mathbb{R}{{\left[ \underline{X} \right]}^{2}}}$ in the polynomial ring
$\sum{\mathbb{R}{{\left[ \underline{X} \right]}^{2}}}$ in the polynomial ring 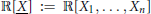 $\mathbb{R}\left[ \underline{X} \right]\,:=\,\mathbb{R}\left[ {{X}_{1}},\,.\,.\,.\,,\,{{X}_{n}} \right]$ in the topology induced by the
$\mathbb{R}\left[ \underline{X} \right]\,:=\,\mathbb{R}\left[ {{X}_{1}},\,.\,.\,.\,,\,{{X}_{n}} \right]$ in the topology induced by the 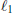 $~{{\ell }_{1}}$-norm is equal to
$~{{\ell }_{1}}$-norm is equal to 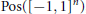 $\text{Pos}\left( {{\left[ -1,\,1 \right]}^{n}} \right)$, the cone consisting of all polynomials that are non-negative on the hypercube
$\text{Pos}\left( {{\left[ -1,\,1 \right]}^{n}} \right)$, the cone consisting of all polynomials that are non-negative on the hypercube 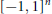 ${{\left[ -1,\,1 \right]}^{n}}$. The result is deduced as a corollary of a general result, established in the same paper, which is valid for any commutative semigroup. In later work, Berg and Maserick and Berg, Christensen, and Ressel establish an even more general result, for a commutative semigroup with involution, for the closure of the cone of sums of squares of symmetric elements in the weighted
${{\left[ -1,\,1 \right]}^{n}}$. The result is deduced as a corollary of a general result, established in the same paper, which is valid for any commutative semigroup. In later work, Berg and Maserick and Berg, Christensen, and Ressel establish an even more general result, for a commutative semigroup with involution, for the closure of the cone of sums of squares of symmetric elements in the weighted 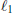 $~{{\ell }_{1}}$-seminorm topology associated with an absolute value. In this paper we give a new proof of these results, which is based on Jacobi’s representation theorem from 2001. At the same time, we use Jacobi’s representation theorem to extend these results from sums of squares to sums of
$~{{\ell }_{1}}$-seminorm topology associated with an absolute value. In this paper we give a new proof of these results, which is based on Jacobi’s representation theorem from 2001. At the same time, we use Jacobi’s representation theorem to extend these results from sums of squares to sums of 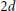 $2d$-powers, proving, in particular, that for any integer
$2d$-powers, proving, in particular, that for any integer 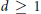 $d\,\ge \,1$, the closure of the cone of sums of
$d\,\ge \,1$, the closure of the cone of sums of 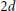 $2d$-powers
$2d$-powers 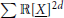 $\sum \mathbb{R}{{\left[ \underline{X} \right]}^{2d}}$ in the
$\sum \mathbb{R}{{\left[ \underline{X} \right]}^{2d}}$ in the 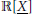 $\mathbb{R}\left[ \underline{X} \right]$ topology induced by the
$\mathbb{R}\left[ \underline{X} \right]$ topology induced by the 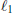 $~{{\ell }_{1}}$-norm is equal to
$~{{\ell }_{1}}$-norm is equal to 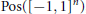 $\text{Pos}\left( {{\left[ -1,\,1 \right]}^{n}} \right)$.
$\text{Pos}\left( {{\left[ -1,\,1 \right]}^{n}} \right)$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
- 4
- Cited by




