No CrossRef data available.
Article contents
On Semisimple Hopf Algebras of Dimension pqn
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 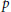 $p$,
$p$, 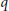 $q$ be prime numbers with
$q$ be prime numbers with 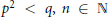 ${{p}^{2}}\,<\,q,\,n\,\in \,\mathbb{N}$, and
${{p}^{2}}\,<\,q,\,n\,\in \,\mathbb{N}$, and  $H$ a semisimple Hopf algebra of dimension
$H$ a semisimple Hopf algebra of dimension 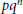 $p{{q}^{n}}$ over an algebraically closed field of characteristic 0. This paper proves that
$p{{q}^{n}}$ over an algebraically closed field of characteristic 0. This paper proves that  $H$ must possess one of the following two structures: (1)
$H$ must possess one of the following two structures: (1)  $H$ is semisolvable; (2)
$H$ is semisolvable; (2)  $H$ is a Radford biproduct
$H$ is a Radford biproduct 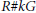 $R\#kG$, where
$R\#kG$, where 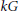 $kG$ is the group algebra of group
$kG$ is the group algebra of group  $G$ of order
$G$ of order 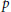 $p$ and
$p$ and 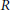 $R$ is a semisimple Yetter–Drinfeld Hopf algebra in
$R$ is a semisimple Yetter–Drinfeld Hopf algebra in 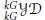 $_{kG}^{kG}y\mathcal{D}$ of dimension
$_{kG}^{kG}y\mathcal{D}$ of dimension 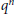 ${{q}^{n}}$.
${{q}^{n}}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
Footnotes
This work was partially supported by the NSF of China (11201231), the China Postdoctoral Science Foundation (2012M511643), the Jiangsu Planned Projects for Postdoctoral Research Funds (1102041C), and the Agricultural Machinery Bureau Foundation of Jiangsu Province (GXZ11003).




