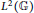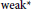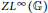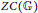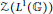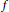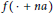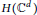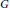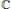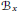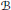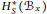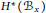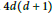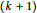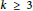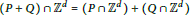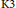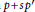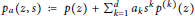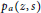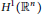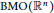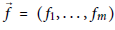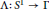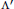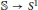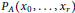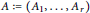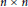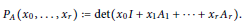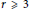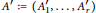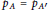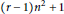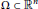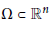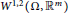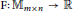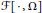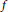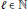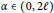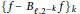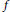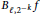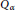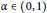Research Article
Character Density in Central Subalgebras of Compact Quantum Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-461
-
- Article
-
- You have access
- Export citation
Functions Universal for all Translation Operators in Several Complex Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 462-469
-
- Article
-
- You have access
- Export citation
Maurer–Cartan Elements in the Lie Models of Finite Simplicial Complexes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 470-477
-
- Article
-
- You have access
- Export citation
Springer's Weyl Group Representation via Localization
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-483
-
- Article
-
- You have access
- Export citation
A Note on Lawton's Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 484-489
-
- Article
-
- You have access
- Export citation
A Riemann–Hurwitz Theorem for the Algebraic Euler Characteristic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 490-509
-
- Article
-
- You have access
- Export citation
Convex-normal (Pairs of) Polytopes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 510-521
-
- Article
-
- You have access
- Export citation
On the Singular Sheaves in the Fine Simpson Moduli Spaces of 1-dimensional Sheaves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 522-535
-
- Article
-
- You have access
- Export citation
The Gradient of a Solution of the Poisson Equation in the Unit Ball and Related Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 536-545
-
- Article
-
- You have access
- Export citation
On Polarized K3 Surfaces of Genus 33
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 546-560
-
- Article
-
- You have access
- Export citation
Nuij Type Pencils of Hyperbolic Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-570
-
- Article
-
- You have access
- Export citation
Weak Factorizations of the Hardy Space H1(ℝn) in Terms of Multilinear Riesz Transforms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 571-585
-
- Article
-
- You have access
- Export citation
Endpoint Regularity of Multisublinear Fractional Maximal Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 586-603
-
- Article
-
- You have access
- Export citation
Stackings and the W-cycles Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 604-612
-
- Article
-
- You have access
- Export citation
On the Dimension of the Locus of Determinantal Hypersurfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 613-630
-
- Article
-
- You have access
- Export citation
Traceless Maps as the Singular Minimizers in the Multi-dimensional Calculus of Variations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 631-640
-
- Article
-
- You have access
- Export citation
Mixed ƒ-divergence for Multiple Pairs of Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 641-654
-
- Article
-
- You have access
- Export citation
Characterizations of Besov-Type and Triebel–Lizorkin–Type Spaces via Averages on Balls
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 655-672
-
- Article
-
- You have access
- Export citation