Article contents
Characterizations of Besov-Type and Triebel–Lizorkin–Type Spaces via Averages on Balls
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 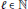 $\ell \in \mathbb{N}$ and
$\ell \in \mathbb{N}$ and 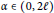 $\alpha \in (0,2\ell )$. In this article, the authors establish equivalent characterizations of Besov-type spaces, Triebel–Lizorkin-type spaces, and Besov–Morrey spaces via the sequence
$\alpha \in (0,2\ell )$. In this article, the authors establish equivalent characterizations of Besov-type spaces, Triebel–Lizorkin-type spaces, and Besov–Morrey spaces via the sequence 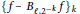 ${{\{f-{{B}_{\ell ,{{2}^{-k}}}}f\}}_{k}}$ consisting of the difference between
${{\{f-{{B}_{\ell ,{{2}^{-k}}}}f\}}_{k}}$ consisting of the difference between 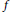 $f$ and the ball average
$f$ and the ball average 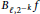 ${{B}_{\ell ,{{2}^{-k}}}}f$. These results lead to the introduction of Besov-type spaces, Triebel–Lizorkin-type spaces, and Besov–Morrey spaceswith any positive smoothness order onmetricmeasure spaces. As special cases, the authors obtain a new characterization of Morrey–Sobolev spaces and
${{B}_{\ell ,{{2}^{-k}}}}f$. These results lead to the introduction of Besov-type spaces, Triebel–Lizorkin-type spaces, and Besov–Morrey spaceswith any positive smoothness order onmetricmeasure spaces. As special cases, the authors obtain a new characterization of Morrey–Sobolev spaces and 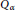 ${{\text{Q}}_{\alpha }}$ spaces with
${{\text{Q}}_{\alpha }}$ spaces with 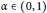 $\alpha \in (0,1)$, which are of independent interest.
$\alpha \in (0,1)$, which are of independent interest.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 11
- Cited by


