Article contents
Nuij Type Pencils of Hyperbolic Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
Nuij's theorem states that if a polynomial 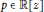 $p\in \mathbb{R}[z]$ is hyperbolic (i.e., has only real roots), then
$p\in \mathbb{R}[z]$ is hyperbolic (i.e., has only real roots), then 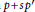 $p+s{{p}^{'}}$ is also hyperbolic for any
$p+s{{p}^{'}}$ is also hyperbolic for any 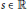 $s\in \mathbb{R}$. We study other perturbations of hyperbolic polynomials of the form
$s\in \mathbb{R}$. We study other perturbations of hyperbolic polynomials of the form 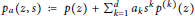 ${{p}_{a}}(z,s)\,\,:=\,\,\,p\,(z)+\,\sum\nolimits_{k=1}^{d}{{{a}_{k}}{{s}^{k}}{{p}^{(k)}}(z)}$. We give a full characterization of those
${{p}_{a}}(z,s)\,\,:=\,\,\,p\,(z)+\,\sum\nolimits_{k=1}^{d}{{{a}_{k}}{{s}^{k}}{{p}^{(k)}}(z)}$. We give a full characterization of those 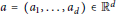 $a=({{a}_{1}},...,{{a}_{d}})\,\in \,{{\mathbb{R}}^{d}}$ for which
$a=({{a}_{1}},...,{{a}_{d}})\,\in \,{{\mathbb{R}}^{d}}$ for which 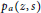 ${{p}_{a}}(z,s)$ is a pencil of hyperbolic polynomials. We also give a full characterization of those
${{p}_{a}}(z,s)$ is a pencil of hyperbolic polynomials. We also give a full characterization of those 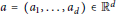 $a=({{a}_{1}},...,{{a}_{d}})\,\in \,{{\mathbb{R}}^{d}}$ for which the associated families
$a=({{a}_{1}},...,{{a}_{d}})\,\in \,{{\mathbb{R}}^{d}}$ for which the associated families 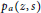 $ $ admit universal determinantal representations. In fact, we show that all these sequences come fromspecial symmetric Toeplitz matrices.
$ $ admit universal determinantal representations. In fact, we show that all these sequences come fromspecial symmetric Toeplitz matrices.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 1
- Cited by




