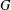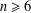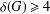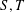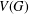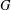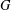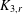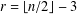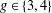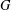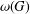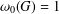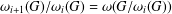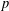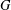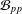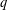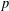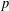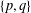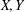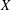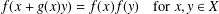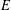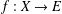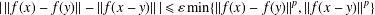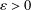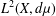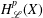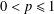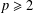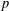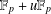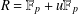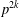Research Article
A NOTE ON ALMOST BALANCED BIPARTITIONS OF A GRAPH
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2014, pp. 177-182
-
- Article
-
- You have access
- Export citation
FINITE 3-GEODESIC TRANSITIVE BUT NOT 3-ARC TRANSITIVE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2014, pp. 183-190
-
- Article
-
- You have access
- Export citation
MULTIPLICITY AND ŁOJASIEWICZ EXPONENT OF GENERIC LINEAR SECTIONS OF MONOMIAL IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2015, pp. 191-201
-
- Article
-
- You have access
- Export citation
RADICAL RELATED TO SPECIAL ATOMS REVISITED
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2014, pp. 202-210
-
- Article
-
- You have access
- Export citation
(ANTI)COMMUTATIVE ALGEBRAS WITH A MULTIPLICATIVE BASIS
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 211-218
-
- Article
-
- You have access
- Export citation
ON THE
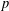 $p$-LENGTH AND THE WIELANDT SERIES OF A FINITE
$p$-LENGTH AND THE WIELANDT SERIES OF A FINITE 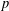 $p$-SOLUBLE GROUP
$p$-SOLUBLE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 09 December 2014, pp. 219-226
-
- Article
-
- You have access
- Export citation
ON THE PRIME GRAPH OF SIMPLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2014, pp. 227-240
-
- Article
-
- You have access
- Export citation
ON SETS OF PP-GENERATORS OF FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2014, pp. 241-249
-
- Article
-
- You have access
- Export citation
EMBEDDABILITY OF GENERALISED WREATH PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 250-263
-
- Article
-
- You have access
- Export citation
A NOTE ON NATURALLY ORDERED SEMIGROUPS OF TRANSFORMATIONS WITH INVARIANT SET
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2014, pp. 264-267
-
- Article
-
- You have access
- Export citation
A VERSION OF ROUCHÉ’S THEOREM FOR CONTINUOUS FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 December 2014, pp. 268-272
-
- Article
-
- You have access
- Export citation
CONTINUOUS ON RAYS SOLUTIONS OF A GOŁA̧B–SCHINZEL TYPE EQUATION
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 273-277
-
- Article
-
- You have access
- Export citation
ON HYPERSTABILITY OF ADDITIVE MAPPINGS ONTO BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 30 December 2014, pp. 278-285
-
- Article
-
- You have access
- Export citation
MAXIMAL HARDY SPACES ASSOCIATED TO NONNEGATIVE SELF-ADJOINT OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 286-302
-
- Article
-
- You have access
- Export citation
FRAGMENTABILITY BY THE DISCRETE METRIC
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2015, pp. 303-310
-
- Article
-
- You have access
- Export citation
SOME COMMENTS ON SCALAR DIFFERENTIATION OF VECTOR-VALUED FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 311-321
-
- Article
-
- You have access
- Export citation
A JORDAN-LIKE DECOMPOSITION IN THE NONCOMMUTATIVE SCHWARTZ SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 322-330
-
- Article
-
- You have access
- Export citation
SUCCESSIVE RADII OF FAMILIES OF CONVEX BODIES
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 331-344
-
- Article
-
- You have access
- Export citation
NOTE ON SUPPORT WEIGHT DISTRIBUTION OF LINEAR CODES OVER
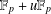 $\mathbb{F}_{p}+u\mathbb{F}_{p}$
$\mathbb{F}_{p}+u\mathbb{F}_{p}$
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2015, pp. 345-350
-
- Article
-
- You have access
- Export citation
Addendum
‘COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK’
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2015, pp. 351-352
-
- Article
-
- You have access
- Export citation