Research Article
One level density of low-lying zeros of families of L-functions
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2010, pp. 1-18
-
- Article
-
- You have access
- Export citation
On mean values and non-vanishing of derivatives of L-functions in a nonlinear family
- Part of:
-
- Published online by Cambridge University Press:
- 20 April 2010, pp. 19-34
-
- Article
-
- You have access
- Export citation
A non-abelian Stickelberger theorem
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2010, pp. 35-55
-
- Article
-
- You have access
- Export citation
Refined class number formulas and Kolyvagin systems
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2010, pp. 56-74
-
- Article
-
- You have access
- Export citation
On the discrete logarithm problem in elliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 15 October 2010, pp. 75-104
-
- Article
-
- You have access
- Export citation
Bimodules and branes in deformation quantization
- Part of:
-
- Published online by Cambridge University Press:
- 11 August 2010, pp. 105-160
-
- Article
-
- You have access
- Export citation
Geometrically rational real conic bundles and very transitive actions
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2010, pp. 161-187
-
- Article
-
- You have access
- Export citation
The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2010, pp. 188-234
-
- Article
-
- You have access
- Export citation
Some complements to the Lazard isomorphism
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2010, pp. 235-262
-
- Article
-
- You have access
- Export citation
A Satake isomorphism in characteristic p
- Part of:
-
- Published online by Cambridge University Press:
- 23 August 2010, pp. 263-283
-
- Article
-
- You have access
- Export citation
The rank of a hypergeometric system
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2010, pp. 284-318
-
- Article
-
- You have access
- Export citation
Greatest lower bounds on the Ricci curvature of Fano manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2010, pp. 319-331
-
- Article
-
- You have access
- Export citation
Corrigenda
Corrigendum: ‘On certain algebraic curves related to polynomial maps, Compositio Math. 103 (1996), 319–350’
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2010, pp. 332-334
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 147 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 January 2011, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
COM volume 147 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 January 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation




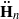 of type GL
of type GL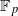 . Assuming that Φ
. Assuming that Φ