Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-06T19:49:15.662Z Has data issue: false hasContentIssue false
  • English
  • Français

The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials

Part of: Curves Arithmetic algebraic geometry Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  07 July 2010

O. Schiffmann  and
E. Vasserot
O. Schiffmann
Affiliation:
Institut Mathématique de Jussieu, Université de Paris 6, 175 rue du Chevaleret, 75013 Paris, France (email: olive@math.jussieu.fr)
E. Vasserot
Affiliation:
Institut Mathématique de Jussieu, Université de Paris 7, 175 rue du Chevaleret, 75013 Paris, France (email: vasserot@math.jussieu.fr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

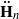We exhibit a strong link between the Hall algebra HX of an elliptic curve X defined over a finite field 𝔽l (or, more precisely, its spherical subalgebra U+X) and Cherednik’s double affine Hecke algebras of type GLn, for all n. This allows us to obtain a geometric construction of the Macdonald polynomials Pλ(q,t−1) in terms of certain functions (Eisenstein series) on the moduli space of semistable vector bundles on the elliptic curve X.

Keywords

Hall algebraselliptic curvesMacdonald polynomialsEisenstein seriesCherednik algebras

MSC classification

Secondary: 17B37: Quantum groups (quantized enveloping algebras) and related deformations 14H05: Algebraic functions; function fields 11G20: Curves over finite and local fields
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 1 , January 2011 , pp. 188 - 234
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Atiyah, M., Vector bundles over an elliptic curve, Proc. Lond. Math. Soc. (3) 7 (1957), 414–452.Google Scholar
[2]Bergeron, F., Garsia, A. M., Haiman, M. and Tesler, G., Identities and positivity conjectures for some remarkable operators in the theory of symmetric functions, Methods Appl. Anal. 6 (1999), 363–420.CrossRefGoogle Scholar
[3]Burban, I. and Schiffmann, O., On the Hall algebra of an elliptic curve, I, Preprint (2005), arXiv:math.AG/0505148.Google Scholar
[4]Cherednik, I., Double affine Hecke algebras (Cambridge University Press, Cambridge, 2004).Google Scholar
[5]Ginzburg, V., Perverse sheaves on loop groups and Langlands duality, Preprint (1995), arXiv:alg-geom/9511007.Google Scholar
[6]Green, J. A., Hall algebras, hereditary algebras and quantum groups, Invent. Math. 120 (1995), 361–377.CrossRefGoogle Scholar
[7]Haiman, M., Notes on Macdonald polynomials and the geometry of Hilbert schemes, in Symmetric functions 2001: surveys of developments and perspectives (Proceedings of the NATO Advanced Study Institute held in Cambridge, June 25 to July 6, 2001) (Kluwer, Dordrecht, 2002), 1–64.Google Scholar
[8]Harder, G., Chevalley groups over function fields and automorphic forms, Ann. of Math. (2) 100 (1974), 249–300.Google Scholar
[9]Ion, B., Involutions of double affine Hecke algebras, Compositio Math. 139 (2003), 67–84.CrossRefGoogle Scholar
[10]Iwahori, N and Matsumoto, H., On some Bruhat decomposition and the structure of Hecke rings of p-adic Chevalley groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 5–48.Google Scholar
[11]Kapranov, M., Eisenstein series and quantum affine algebras, J. Math. Sci. 84 (1997), 1311–1360.CrossRefGoogle Scholar
[12]Laumon, G., Faisceaux automorphes liés aux séries d’Eisenstein, in Automorphic forms, Shimura varieties and L-functions, Perspectives in Mathematics, vol. 10 (Academic Press, Boston, 1990), 227–279.Google Scholar
[13]Lusztig, G., Green polynomials and singularities of unipotent classes, Adv. Math. 42 (1981), 169–178.Google Scholar
[14]Macdonald, I. G., Symmetric functions and Hall polynomials, Oxford Mathematical Monographs second edition (Clarendon Press, Oxford, 1995).Google Scholar
[15]Macdonald, I. G., A new class of symmetric functions, Actes du 20e séminaire Lotharingien, Publ. I.R.M.A. Strasbourg (1988), 131–171.Google Scholar
[16]Mirkovic, I. and Vilonen, K., Perverse sheaves on affine Grassmannians and Langlands duality, Math. Res. Lett. 7 (2000), 13–24.CrossRefGoogle Scholar
[17]Polishchuk, A., Abelian varieties, theta functions and the Fourier transform (Cambridge University Press, Cambridge, 2003).Google Scholar
[18]Ringel, C., Hall algebras and quantum groups, Invent. Math. 101 (1990), 583–591.CrossRefGoogle Scholar
[19]Schiffmann, O., On the Hall algebra of an elliptic curve, II, Preprint (2005), arXiv:math/0508553.Google Scholar
[20]Schiffmann, O. and Vasserot, E., The elliptic Hall algebra and the K-theory of the Hilbert scheme of points of 𝔸2, Preprint (2009), arXiv:0905.2555.Google Scholar
[21]Weyl, H., The classical groups, their invariants and representations (Princeton University Press, Princeton, NJ, 1949).Google Scholar