Research Article
Convex bodies equidecomposable by locally discrete groups of isometries
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
Isoperimetric problems for tilings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-15
-
- Article
- Export citation
The distribution of exponential sums
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 16-25
-
- Article
- Export citation
Solution of a problem of Knuth on complete uniform distribution of sequences
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 26-32
-
- Article
- Export citation
On an extremal property of the Rudin-Shapiro sequence
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-38
-
- Article
- Export citation
An upper bound for the index of χ-irregularity
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-44
-
- Article
- Export citation
A note on the integral points of a modular curve of level 7
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-48
-
- Article
- Export citation
Free actions on (Sn)k
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-54
-
- Article
- Export citation
Cohomology of Bieberbach groups
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-59
-
- Article
- Export citation
Functions and measures on products spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-67
-
- Article
- Export citation
Extending classical criteria for differentiation theorems
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-74
-
- Article
- Export citation
Perturbation theory for a displacement front passing discontinuities in capillary pressure and permeability in a porous medium
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-89
-
- Article
- Export citation
Thinness and boundary behaviour of potentials for the heat equation
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 90-95
-
- Article
- Export citation
Singularities of bessel-zeta functions and Hawkins' polynomials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 96-103
-
- Article
- Export citation
Zeros of generalized Airy functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 104-117
-
- Article
- Export citation
On transformations of the biharmonic equation
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-130
-
- Article
- Export citation
The asymptotic solution of linear differential systems
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-138
-
- Article
- Export citation
On Hayman's alternative
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-146
-
- Article
- Export citation
Separation of K–analytic sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-190
-
- Article
- Export citation
Front matter
MTK volume 32 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation



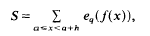
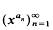 is completely uniformly distributed modulo 1 for almost all real numbers
is completely uniformly distributed modulo 1 for almost all real numbers 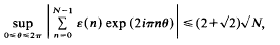
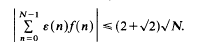
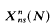 . denote the modular curve associated with the normalizer of a non-split Cartan group of level
. denote the modular curve associated with the normalizer of a non-split Cartan group of level 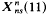 has genus 1. Ligozat [5] has shown that the group of Q-rational points on
has genus 1. Ligozat [5] has shown that the group of Q-rational points on  , the following theorem holds.
, the following theorem holds.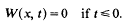
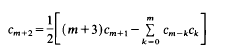
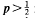 is extended to show that all the zeros of
is extended to show that all the zeros of 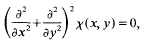
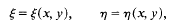
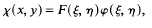
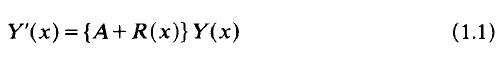

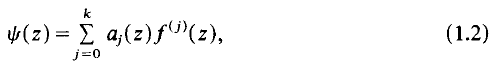
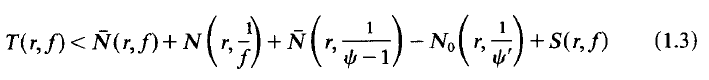
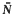
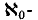 analytic sets developed by Stone and Hansell. As we explain in [5], this theory parallels the recently developed theory of Frolík and Holický, but has certain advantages. In this paper we take the theory rather further, and, in particular, we prove a number of variants of Lusin's first separation theorem and give some of their applications. We make free use of the definitions, notation and conventions introduced in [5].
analytic sets developed by Stone and Hansell. As we explain in [5], this theory parallels the recently developed theory of Frolík and Holický, but has certain advantages. In this paper we take the theory rather further, and, in particular, we prove a number of variants of Lusin's first separation theorem and give some of their applications. We make free use of the definitions, notation and conventions introduced in [5].