Article contents
Zeros of generalized Airy functions
Published online by Cambridge University Press: 26 February 2010
Extract
Some interlacing properties of the zeros of the generalized Airy functions A1(z, p) are given for non-positive integral values of p. The result that A1 (z,p) has no real zero for 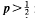 is extended to show that all the zeros of A1(z,p) are real and simple if
is extended to show that all the zeros of A1(z,p) are real and simple if 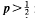 . It is also shown that all the zeros of the functions Bk(z,p, 1) for k = 1, 2, 3 are simple for non-positive integral p.
. It is also shown that all the zeros of the functions Bk(z,p, 1) for k = 1, 2, 3 are simple for non-positive integral p.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1985
References
- 4
- Cited by




