Article contents
On an extremal property of the Rudin-Shapiro sequence
Published online by Cambridge University Press: 26 February 2010
Abstract
Extending the well-known property of the Rudin- Shapiro sequence ε = (ε(n)) with values in {−1, +1} satisfying
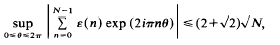
we show that for all unimodular 2-multiplicative sequences f = (f(n))
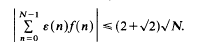
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1985
References
- 6
- Cited by


