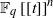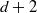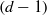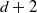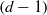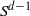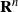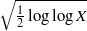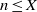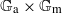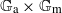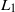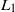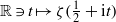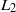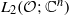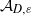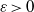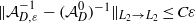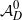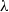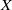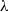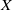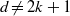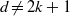Research Article
KAKEYA SETS OVER NON-ARCHIMEDEAN LOCAL RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2013, pp. 257-266
-
- Article
- Export citation
ALMOST ALL SETS OF
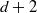 $d+ 2$ POINTS ON THE
$d+ 2$ POINTS ON THE 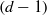 $(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
$(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2013, pp. 267-268
-
- Article
- Export citation
DISSOLVING OF CUSP FORMS: HIGHER-ORDER FERMI’S GOLDEN RULES
- Part of:
-
- Published online by Cambridge University Press:
- 21 January 2013, pp. 269-301
-
- Article
- Export citation
ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER
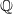 $\mathbb {Q}$
$\mathbb {Q}$
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2013, pp. 303-319
-
- Article
- Export citation
ZERO-ONE LAWS IN SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 21 January 2013, pp. 321-332
-
- Article
- Export citation
A SMALL VALUE ESTIMATE FOR
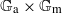 $\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
$\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2013, pp. 333-363
-
- Article
- Export citation
LOWER BOUNDS FOR
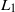 ${L}_{1} $ DISCREPANCY
${L}_{1} $ DISCREPANCY
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2013, pp. 365-379
-
- Article
- Export citation
THE VALUE DISTRIBUTION OF INCOMPLETE GAUSS SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2013, pp. 381-398
-
- Article
- Export citation
ON A CONJECTURE OF IGUSA
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 399-425
-
- Article
- Export citation
THE DISTRIBUTION OF THE MAXIMUM OF CHARACTER SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2013, pp. 427-442
-
- Article
- Export citation
NEGATIVE VALUES OF THE RIEMANN ZETA FUNCTION ON THE CRITICAL LINE
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2013, pp. 443-462
-
- Article
- Export citation
HOMOGENIZATION OF THE DIRICHLET PROBLEM FOR ELLIPTIC SYSTEMS:
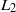 $L_2$-OPERATOR ERROR ESTIMATES
$L_2$-OPERATOR ERROR ESTIMATES
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2013, pp. 463-476
-
- Article
- Export citation
INTERSECTIONS OF BALLS AND SETS OF CONSTANT WIDTH IN FINITE-DIMENSIONAL NORMED SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2013, pp. 477-492
-
- Article
- Export citation
ON POLYTOPAL UPPER BOUND SPHERES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2013, pp. 493-496
-
- Article
- Export citation
SUBGROUPS OF FRACTIONAL DIMENSION IN NILPOTENT OR SOLVABLE LIE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2013, pp. 497-511
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK VOLUME 59 ISSUE 2 COVER AND FRONT MATTER
-
- Published online by Cambridge University Press:
- 05 July 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
MTK VOLUME 59 ISSUE 2 COVER AND BACK MATTER
-
- Published online by Cambridge University Press:
- 05 July 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation