Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-16T17:58:09.277Z Has data issue: false hasContentIssue false
  • English
  • Français

ON POLYTOPAL UPPER BOUND SPHERES

Part of: Polytopes and polyhedra

Published online by Cambridge University Press:  28 March 2013

Bhaskar Bagchi  and
Basudeb Datta
Bhaskar Bagchi
Affiliation:
Theoretical Statistics and Mathematics Unit, Indian Statistical Institute, Bangalore 560059,India email bbagchi@isibang.ac.in
Basudeb Datta
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore 560012,India email dattab@math.iisc.ernet.in
Get access

Abstract

Generalizing a result (the case 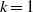$k= 1$) due to M. A. Perles, we show that any polytopal upper bound sphere of odd dimension 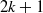$2k+ 1$ belongs to the generalized Walkup class 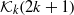${ \mathcal{K} }_{k} (2k+ 1)$, i.e., all its vertex links are 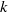$k$-stacked spheres. This is surprising since it is far from obvious that the vertex links of polytopal upper bound spheres should have any special combinatorial structure. It has been conjectured that for 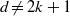$d\not = 2k+ 1$, all 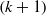$(k+ 1)$-neighborly members of the class 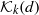${ \mathcal{K} }_{k} (d)$ are tight. The result of this paper shows that the hypothesis 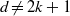$d\not = 2k+ 1$ is essential for every value of 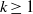$k\geq 1$.

MSC classification

Secondary: 52B11: $n$-dimensional polytopes 52B05: Combinatorial properties (number of faces, shortest paths, etc.) 52B22: Shellability
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 493 - 496
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altshuler, A. and Steinberg, L., Neighborly 4-polytopes with 9 vertices. J. Combin. Theory Ser. A 15 (1973), 270–287.CrossRefGoogle Scholar
Bagchi, B. and Datta, B., Lower bound theorem for normal pseudomanifolds. Exp. Math. 26 (2008), 327–351.CrossRefGoogle Scholar
Bagchi, B. and Datta, B., On stellated spheres, shellable balls, lower bounds and a combinatorial criterion for tightness, Preprint, 2011, arXiv:1102.0856v2.Google Scholar
Bagchi, B. and Datta, B., On stellated spheres and a tightness criterion for combinatorial manifolds. Preprint, 2012, arXiv:1207.5599v1.Google Scholar
Grünbaum, B., Convex Polytopes, 2nd edn(Graduate Texts in Mathematics 221), Springer (New York, 2003).CrossRefGoogle Scholar
McMullen, P., On simple polytopes. Invent. Math. 113 (1993), 419–444.CrossRefGoogle Scholar
McMullen, P. and Walkup, D. W., A generalized lower-bound conjecture for simplicial polytopes. Mathematika 18 (1971), 264–273.CrossRefGoogle Scholar
Murai, S. and Nevo, E., On the generalized lower bound conjecture for polytopes and spheres, Acta. Math. (to appear).Google Scholar
Novik, I., Upper bound theorems for homology manifolds. Israel J. Math. 108 (1998), 45–82.CrossRefGoogle Scholar
Stanley, R. P., The number of faces of a simplicial convex polytope. Adv. Math. 11 (1980), 236–238.CrossRefGoogle Scholar
Ziegler, G. M., Lectures on Polytopes, Springer (New York, 1995).CrossRefGoogle Scholar