Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-25T13:56:54.663Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERSECTIONS OF BALLS AND SETS OF CONSTANT WIDTH IN FINITE-DIMENSIONAL NORMED SPACES

Part of: General convexity Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  28 March 2013

Horst Martini ,
Christian Richter  and
Margarita Spirova
Horst Martini
Affiliation:
Technische Universität Chemnitz, Fakultät für Mathematik, D-09107 Chemnitz,Germany email horst.martini@mathematik.tu-chemnitz.de
Christian Richter
Affiliation:
Friedrich-Schiller-Universität Jena, Mathematisches Institut, D-07737 Jena,Germany email christian.richter@uni-jena.de
Margarita Spirova
Affiliation:
Technische Universität Chemnitz, Fakultät für Mathematik, D-09107 Chemnitz,Germany email margarita.spirova@mathematik.tu-chemnitz.de
Get access

Abstract

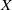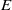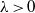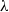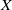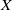For an arbitrary subset $X$ of a finite-dimensional real Banach space $E$, the ball intersection with parameter $\lambda \gt 0$ is defined as the intersection of all balls of radius $\lambda $ whose centers are in $X$. On the other hand, the intersection of all balls of radius $\lambda $ that contain $X$ is said to be the respective ball hull. We present new results on these two notions and use them to get new insights into complete sets and (pairs of) sets of constant width, e.g., their representation as vector sums of suitable ball intersections and ball hulls. Also in this framework, we give partial answers to the known question, in what finite-dimensional real Banach spaces any complete set is of constant width. For polyhedral norms we obtain characterizations of monotypic balls via constant width properties of pairs formed by the ball intersection and ball hull of the same bounded and non-empty set. Finally, we present some new results on Borsuk numbers of sets of constant width in normed spaces, closely related to (unique) completions of compact sets. For example, the lower estimate on Borsuk numbers of bodies of constant width due to Lenz is extended to arbitrary normed spaces. Furthermore, we also derive the Borsuk number of the normed space with maximum norm.

MSC classification

Secondary: 46B20: Geometry and structure of normed linear spaces 52A10: Convex sets in $2$ dimensions (including convex curves) 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52A21: Finite-dimensional Banach spaces (including special norms, zonoids, etc.)
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 477 - 492
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baronti, M. and Papini, L. P., Diameters, centers and diametrically maximal sets. Rend. Circ. Mat. Palermo (2) Suppl. 38 (1995), 11–24.Google Scholar
Boltyanski, V., Martini, H. and Soltan, P. S., Excursions into Combinatorial Geometry, Springer (Berlin, 1997).CrossRefGoogle Scholar
Boltyanski, V. and Soltan, V. P., Borsuk’s problem. Mat. Zametki 22 (1977), 621–631 (in Russian).Google Scholar
Borowska, D. and Grzybowski, J., The intersection property in the family of compact convex sets. J. Convex Anal. 17 (2010), 173–181.Google Scholar
Chakerian, G. D. and Groemer, H., Convex bodies of constant width. In Convexity and Its Applications (eds Gruber, P. M. and Wills, J. M.),Birhäuser (Basel, 1983), 49–96.CrossRefGoogle Scholar
Eggleston, H. G., Sets of constant width in finite dimensional Banach spaces. Israel J. Math. 3 (1965), 163–172.CrossRefGoogle Scholar
Goodey, P. R., Intersection of circles and curves of constant width. Math. Ann. 208 (1974), 49–58.CrossRefGoogle Scholar
Goodey, P. R., Intersections of planar convex curves. Math. Ann. 267 (1984), 145–159.CrossRefGoogle Scholar
Groemer, H., On complete convex bodies. Geom. Dedicata 20 (1986), 319–334.CrossRefGoogle Scholar
Grünbaum, B., Borsuk’s partition conjecture in Minkowski planes. Bull. Res. Council Israel Sect. F 7F (1957/1958), 25–30.Google Scholar
Grünbaum, B., Borsuk’s problem and related questions. In Proc. Sympos. Pure Math., Vol. VII, American Mathematical Society (Providence, R.I, 1963), 271–284.Google Scholar
Heil, E. and Martini, H., Special convex bodies. In Handbook of Convex Geometry, Vol. A (eds Gruber, P. M. and Wills, J. M.),North-Holland (Amsterdam, 1993), 347–385.CrossRefGoogle Scholar
Karasëv, R. N., On the characterization of generating sets. Modelir. Anal. Inf. Sist. 8 (2) (2001), 3–9 (in Russian).Google Scholar
Kołodziejczyk, K., Borsuk covering and planar sets with unique completion. Discrete Math. 122 (1993), 235–244.CrossRefGoogle Scholar
Lenz, H., Zur Zerlegung von Punktmengen in solche kleineren Durchmessers. Arch. Math. 6 (1955), 413–416.CrossRefGoogle Scholar
Maehara, H., Convex bodies forming pairs of constant width. J. Geom. 22 (1984), 101–107.CrossRefGoogle Scholar
Martín, P., Martini, H. and Spirova, M., Chebyshev sets and ball operators (submitted).Google Scholar
Martini, H. and Spirova, M., On the circular hull property in normed planes. Acta Math. Hungar. 125 (2009), 275–285.CrossRefGoogle Scholar
Martini, H. and Swanepoel, K. J., The geometry of Minkowski spaces—a survey, Part II. Expo. Math. 22 (2004), 93–144.CrossRefGoogle Scholar
Matoušek, J., Using the Borsuk–Ulam Theorem (Universitext), Springer (Berlin, 2003). Written in cooperation with A. Björner and G. M. Ziegler.Google Scholar
McMullen, P., Schneider, R. and Shephard, G. C., Monotypic polytopes and their intersection properties. Geom. Dedicata 3 (1974), 99–129.CrossRefGoogle Scholar
Moreno, J. P. and Schneider, R., Diametrically complete sets in Minkowski spaces. Israel J. Math. 191 (2012), 701–720.CrossRefGoogle Scholar
Moreno, J. P. and Schneider, R., Local Lipschitz continuity of the diametric completion mapping. Houston J. Math. 38 (2012), 1207–1223.Google Scholar
Peterson, B. B., Intersection properties of curves of constant width. Illinois J. Math. 17 (1973), 411–420.CrossRefGoogle Scholar
Raigorodskii, A. M., Three lectures on the Borsuk partition problem. In Surveys in Contemporary Mathematics (London Mathematical Society Lecture Note Series 347), Cambridge University Press (Cambridge, 2008), 202–247.Google Scholar
Sallee, G. T., Sets of constant width, the spherical intersection property and circumscribed balls. Bull. Aust. Math. Soc. 33 (1986), 369–371.CrossRefGoogle Scholar
Sallee, G. T., Pairs of sets of constant relative width. J. Geom. 29 (1987), 1–11.CrossRefGoogle Scholar
Spirova, M., Discrete Geometry in Normed Spaces, Südwestdeutscher Verlag für Hochschulschriften (Saarbrücken, 2011).Google Scholar
Valentine, F. A., Convex Sets, McGraw-Hill (New York, 1964).Google Scholar
Xu, C., Yuan, L. and Ding, R., Borsuk’s problem in a special normed space. Northeast Math. J. 20 (2004), 79–83.Google Scholar