Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T21:36:10.477Z Has data issue: false hasContentIssue false
  • English
  • Français

KAKEYA SETS OVER NON-ARCHIMEDEAN LOCAL RINGS

Part of: Finite geometry and special incidence structures Designs and configurations

Published online by Cambridge University Press:  28 March 2013

Evan P. Dummit  and
Márton Hablicsek
Evan P. Dummit
Affiliation:
UW-Madison, Department of Mathematics, 480 Lincoln Dr., Madison, WI 53706-1388,U.S.A. email dummit@math.wisc.edu
Márton Hablicsek
Affiliation:
UW-Madison, Department of Mathematics, 480 Lincoln Dr., Madison, WI 53706-1388,U.S.A. email hablics@math.wisc.edu
Get access

Abstract

In a recent paper of Ellenberg, Oberlin, and Tao [The Kakeya set and maximal conjectures for algebraic varieties over finite fields. Mathematika 56 (2010), 1–25], the authors asked whether there are Besicovitch phenomena in 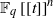${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{n} $. In this paper, we answer their question in the affirmative by explicitly constructing a Kakeya set of measure zero in 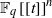${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{n} $. Furthermore, we prove that any Kakeya set in 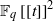${ \mathbb{F} }_{q} \mathop{[[t] ] }\nolimits ^{2} $ or 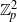${ \mathbb{Z} }_{p}^{2} $ is of Minkowski dimension 2.

MSC classification

Secondary: 05B30: Other designs, configurations 51E20: Combinatorial structures in finite projective spaces
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 257 - 266
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Besicovitch, A., Sur deux questions d’intégrabilité des fonctions. J. Soc. Phys. Math. 2 (1919), 105–123.Google Scholar
Davies, R. O., Some remarks on the Kakeya problem. Proc. Cambridge Phil. Soc. 69 (1971), 417–421.CrossRefGoogle Scholar
Dvir, Z., On the size of Kakeya sets in finite fields. J. Amer. Math. Soc. 22 (2009), 1093–1097.CrossRefGoogle Scholar
Ellenberg, J.  S., Oberlin, R. and Tao, T., The Kakeya set and maximal conjectures for algebraic varieties over finite fields. Mathematika 56 (2010), 1–25.CrossRefGoogle Scholar
Wolff, T., An improved bound for Kakeya type maximal functions. Rev. Mat. Iberoam. 11 (1999), 651–674.Google Scholar