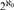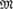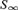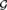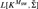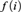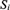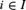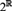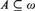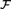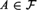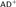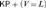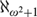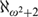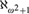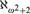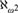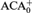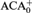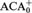Articles
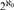 ${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS
${2^{{\aleph _0}}}$ PAIRWISE NONISOMORPHIC MAXIMAL-CLOSED SUBGROUPS OF SYM(ℕ) VIA THE CLASSIFICATION OF THE REDUCTS OF THE HENSON DIGRAPHS
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 395-415
-
- Article
- Export citation
RELATIVELY EXCHANGEABLE STRUCTURES
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 416-442
-
- Article
- Export citation
COMPUTABLE POLISH GROUP ACTIONS
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 443-460
-
- Article
- Export citation
SOME APPLICATIONS OF SUPERCOMPACT EXTENDER BASED FORCINGS TO HOD
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 461-476
-
- Article
- Export citation
ABSTRACT ω-LIMIT SETS
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 477-495
-
- Article
- Export citation
VARSOVIAN MODELS I
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 496-528
-
- Article
- Export citation
UNIFORM PROCEDURES IN UNCOUNTABLE STRUCTURES
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 529-550
-
- Article
- Export citation
ON THE SET-THEORETIC STRENGTH OF ELLIS’ THEOREM AND THE EXISTENCE OF FREE IDEMPOTENT ULTRAFILTERS ON ω
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 551-571
-
- Article
- Export citation
HAPPY AND MAD FAMILIES IN L(ℝ)
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 572-597
-
- Article
- Export citation
ABSTRACT INDUCTIVE AND CO-INDUCTIVE DEFINITIONS
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 598-616
-
- Article
- Export citation
NUMBER SYSTEMS WITH SIMPLICITY HIERARCHIES: A GENERALIZATION OF CONWAY’S THEORY OF SURREAL NUMBERS II
-
- Published online by Cambridge University Press:
- 05 February 2018, pp. 617-633
-
- Article
- Export citation
KEISLER’S ORDER IS NOT LINEAR, ASSUMING A SUPERCOMPACT
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 634-641
-
- Article
- Export citation
ABOUT SOME FIXED POINT AXIOMS AND RELATED PRINCIPLES IN KRIPKE–PLATEK ENVIRONMENTS
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 642-668
-
- Article
- Export citation
THE TREE PROPERTY AT
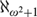 ${\aleph _{{\omega ^2} + 1}}$ AND
${\aleph _{{\omega ^2} + 1}}$ AND 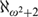 ${\aleph _{{\omega ^2} + 2}}$
${\aleph _{{\omega ^2} + 2}}$
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 669-682
-
- Article
- Export citation
EQUIVALENCE RELATIONS INVARIANT UNDER GROUP ACTIONS
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 683-702
-
- Article
- Export citation
THE COMPLEXITY OF THE EMBEDDABILITY RELATION BETWEEN TORSION-FREE ABELIAN GROUPS OF UNCOUNTABLE SIZE
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 703-716
-
- Article
- Export citation
AVOIDING EFFECTIVE PACKING DIMENSION 1 BELOW ARRAY NONCOMPUTABLE C.E. DEGREES
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 717-739
-
- Article
- Export citation
CONSERVATIVITY OF ULTRAFILTERS OVER SUBSYSTEMS OF SECOND ORDER ARITHMETIC
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 740-765
-
- Article
- Export citation
RANDOMNESS VIA INFINITE COMPUTATION AND EFFECTIVE DESCRIPTIVE SET THEORY
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 766-789
-
- Article
- Export citation
COMPACT CARDINALS AND EIGHT VALUES IN CICHOŃ’S DIAGRAM
-
- Published online by Cambridge University Press:
- 01 August 2018, pp. 790-803
-
- Article
- Export citation